Сверткой функций f(t) и g(t) называют интеграл вида
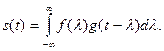 (1.54)
(1.54)
Интегральное преобразование (1.54) часто используется в теоретической радиотехнике [1, 3, 9].
Спектр произведения сигналов (теорема о свертке спектров). Пусть f[t) и g(t) — сигналы со спектральными функциями соответственно. Тогда сигналу s(t) — f(f)-g(t) соответствует спектральная функция
 (1.55)
(1.55)
Спектральная функция произведения сигналов есть свертка их спектральных функций (с коэффициентом 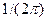 ).
).
Теорема Рэлея. При 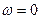 из выражения (1.55) следует теорема Рэлея:
из выражения (1.55) следует теорема Рэлея:
 (1.56)
(1.56)
Здесь учтено соотношение (1.34) 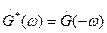 .
.
Равенство Парсеваля. При  из теоремы Рэлея следует равенство Парсеваля
из теоремы Рэлея следует равенство Парсеваля
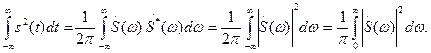 (1.57)
(1.57)
Спектр свертки сигналов. Пусть  и
и 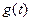 — сигналы со спектральными функциями
— сигналы со спектральными функциями 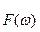 и
и 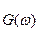 соответственно. Будем искать спектральную функцию свертки (1.54) этих сигналов, для чего представим функцию
соответственно. Будем искать спектральную функцию свертки (1.54) этих сигналов, для чего представим функцию 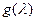 как обратное преобразование Фурье (1.32) спектральной функции
как обратное преобразование Фурье (1.32) спектральной функции 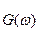 : |
: |
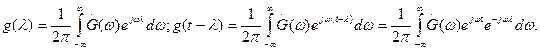
Таким образом,
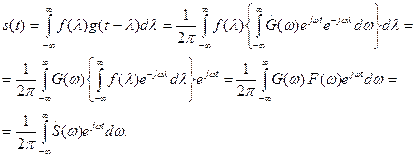
Показано (изменением не влияющего на результат порядка интегрирования в двойном интеграле), что спектральная функция свертки сигналов есть произведение их спектральных функций:
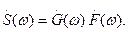 (1.58)
(1.58)
Это важнейшее для дальнейшего изложения соотношение, связывающее, в частности, временной и спектральный подходы к анализу преобразований сигналов в линейных цепях.
1.8. ПРЕОБРАЗОВАНИЕ ФУРЬЕ НЕКОТОРЫХ НЕИНТЕГРИРУЕМЫХ АБСОЛЮТНО СИГНАЛОВ
Математические модели некоторых широко используемых в теоретической радиотехнике сигналов не удовлетворяют условию абсолютной интегрируемости (1.33). Следовательно, преобразование Фурье в обычном виде к ним неприменимо.
Распространить методы преобразования Фурье на сигналы такого рода позволяет использование функции Дирака 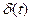 , спектральная характеристика которой была определена в § 1.5.
, спектральная характеристика которой была определена в § 1.5.
Спектральная функция постоянного во времени сигнала. Воспользуемся результатом (1.59) и запишем спектральную функцию постоянного во времени (очевидно, абсолютно неинтегрируемого) сигнала 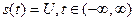 :
:
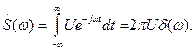 (1.59)
(1.59)
Физический смысл этого результата очевиден — постоянному во времени сигналу соответствует спектр, состоящий из единственной составляющей на нулевой частоте — 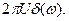
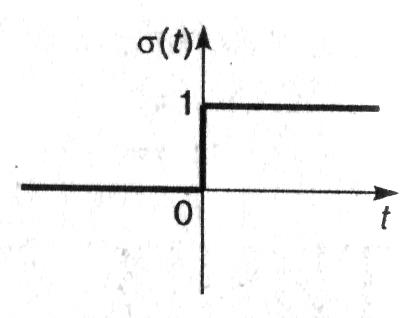
Преобразование Фурье функции Хевисайда. График функции Хевисайда (1.8) показан на рис. 1.10.
Согласно (1.12), производной функции Хевисайда является 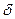 -функция, спектр которой, в соответствии с (1.38), оказывается равным единице:
-функция, спектр которой, в соответствии с (1.38), оказывается равным единице:

Тогда спектральная функция 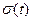 в силу соотношений (1.9) и (1.53) есть
в силу соотношений (1.9) и (1.53) есть
 (1.60)
(1.60)
Спектр сдвинутой во времени функции Хевисайда 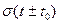 формально следует записывать как
формально следует записывать как

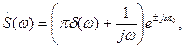
но так как 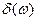 отлична от нуля лишь при
отлична от нуля лишь при 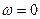 , спектр
, спектр 
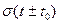 представляют в виде
представляют в виде
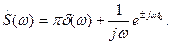 (1.61)
(1.61)
Преобразование Фурье гармонического сигнала. Гармонический сигнал (1.1) также является неинтегрируемой абсолютно функцией. Введем начальную фазу 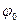 и будем с учетом (1.40) искать спектральную функцию сигнала
и будем с учетом (1.40) искать спектральную функцию сигнала  :
:
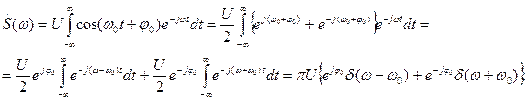 (1.62)
(1.62)
Гармоническому колебанию с конечной амплитудой соответствует спектральная функция с 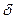 -особенностями в точках
-особенностями в точках 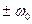 частотной оси. Положив в (1.62)
частотной оси. Положив в (1.62) 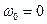 и
и 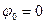 , как частный случай получим уже известный результат (1.59) — спектр постоянного во времени сигнала.
, как частный случай получим уже известный результат (1.59) — спектр постоянного во времени сигнала.
Продемонстрировано использование 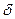 -функции при формальном применении преобразования Фурье к простейшим неинтегрируемым абсолютно сигналам (в частности, к периодическому) и тем самым показана принципиальная возможность единого подхода к спектральному анализу периодических и непериодических сигналов.
-функции при формальном применении преобразования Фурье к простейшим неинтегрируемым абсолютно сигналам (в частности, к периодическому) и тем самым показана принципиальная возможность единого подхода к спектральному анализу периодических и непериодических сигналов.
Замечание 1
Изложенное в некоторых случаях позволяет заметно упростить вычисления; рассмотрим, например, сигнал, представленный как произведение двух функций, каким, по существу, является радиосигнал (1.14)
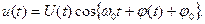
Спектральная функция произведения сигналов рассматривалась в § 1.6. Обозначим через 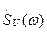 спектр огибающей
спектр огибающей 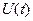 , положим
, положим 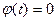 , воспользуемся формулами (1.62) для спектра
, воспользуемся формулами (1.62) для спектра  гармонической функции
гармонической функции 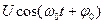 при
при 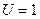 и
и 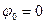 подставим эти спектры в формулу (1.55), полагая
подставим эти спектры в формулу (1.55), полагая 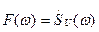 и
и 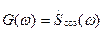 . Тогда спектр радиосигнала
. Тогда спектр радиосигнала 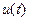 :
:

Использовано фильтрующее свойство 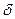 -функции (1.11). Аргументами, при которых существуют
-функции (1.11). Аргументами, при которых существуют 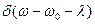 и
и 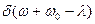 здесь являются соответственно
здесь являются соответственно 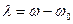 и
и 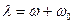 .
.
На функцию U(t) не накладывалось никаких ограничений; в то же время полученное выражение в точности совпадает с результатом (1.44), приобретающим, таким образом, общее значение.
О вычислении спектра сигнала, представленного кусочно-полиномиальной функцией. Если модель финитного сигнала представлена кусочно (на отдельных интервалах) или полностью только функциями вида
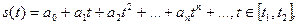
то для вычисления его спектральной функции целесообразно применение процедуры 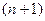 -кратного дифференцирования s(t) с последующим определением спектра производной
-кратного дифференцирования s(t) с последующим определением спектра производной 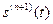 и, с использованием оператора интегрирования в частотной области
и, с использованием оператора интегрирования в частотной области  , собственно спектра сигнала.
, собственно спектра сигнала.
Пример 1. Возьмем прямоугольный видеоимпульс (1.48), являющийся на интервале 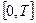 полиномом степени n = 0. Производная сигнала (1.48):
полиномом степени n = 0. Производная сигнала (1.48):
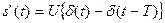
(заметим, что сигнал (1.48) можно трактовать как сумму двух функций Хевисайда, 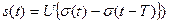 . Спектральная функция первой производной:
. Спектральная функция первой производной:
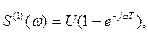
спектральная функция сигнала
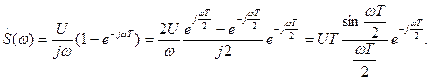
Проще было бы сразу обратиться к формулам (1.60) и (1.61), но здесь речь идет о демонстрации универсального и практически весьма полезного приема, основанного на использовании результатов (1.38) и (1.41) и теорем о спектрах производной и интеграла переменным верхним пределом от сигнала, изложенных в § 1.4.
Так как сигнал является первообразной функцией для своей производной, «площадь» под графиком производной финитного сигнала оказывается равной нулю:

То же справедливо и для производных более высоких порядков. Таким образом, условие (1.52) всегда выполняется.
Сигнал s(t) дифференцируют до тех пор, пока его производная не станет представлять собой последовательность 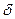 -функций и производных
-функций и производных 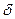 -функций. Процесс дифференцирования удобно сопровождать соответствующими рисунками.
-функций. Процесс дифференцирования удобно сопровождать соответствующими рисунками.
Пример 2. Вычислим спектральную функцию сигнала (1.5), представленного на интервале 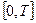 полиномом степени п = 1. Сигнал, его первая и вторая производные показаны на рис. 1.11, а, б, в. Выражение
полиномом степени п = 1. Сигнал, его первая и вторая производные показаны на рис. 1.11, а, б, в. Выражение
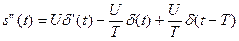
позволяет сразу записать спектральную функцию второй производной:
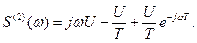
Замечание 2
Производная 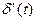 , как и производные
, как и производные 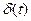 более высоких порядков — понятие физически бессодержательное и его следует воспринимать здесь формально: спектром n-й производной
более высоких порядков — понятие физически бессодержательное и его следует воспринимать здесь формально: спектром n-й производной 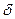 -функции является
-функции является 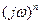 .
.
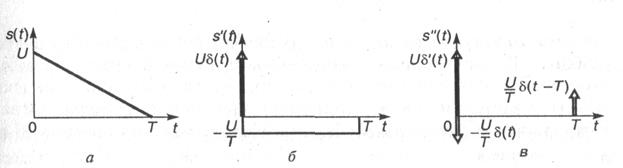
Рис. 1.11. Вычисление спектра треугольного импульса
методом дифференцирования: а — исходный сигнал, б — первая производная, в — вторая производная
Далее, дважды используя оператор интегрирования в частотной области, получаем спектральную функцию сигнала s(t):
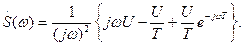
Преобразование полученного для 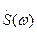 выражения в показательную форму (1.36) и его анализ читателю предлагается выполнить самостоятельно.
выражения в показательную форму (1.36) и его анализ читателю предлагается выполнить самостоятельно.
1.9. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В СПЕКТРАЛЬНОМ АНАЛИЗЕ
Удельная энергия сигнала. Энергетические параметры сигнала вводят, опираясь на следующие положения:
• пусть s(t) есть напряжение или ток; тогда мгновенная мощность сигнала (Вт) определяется как
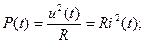
• напряжение действует на активном сопротивлении R= 1 Ом; ток проходит через активное сопротивление R =1 Ом; тогда мгновенная удельная (приходящаяся на 1 Ом) мощность сигнала (Вт) численно определяется как

а удельная энергия сигнала (Дж) равна:
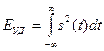 (1.63)
(1.63)
вне зависимости от размерности (В или А) сигнала  , что очень удобно. В дальнейшем при всяком упоминании термина «мощность» или «энергия» определение «удельная», как и индекс «уд», опускается, но (если нет специальных оговорок) подразумевается; так что В2, А2 непосредственно определяют мощность, а
, что очень удобно. В дальнейшем при всяком упоминании термина «мощность» или «энергия» определение «удельная», как и индекс «уд», опускается, но (если нет специальных оговорок) подразумевается; так что В2, А2 непосредственно определяют мощность, а 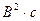 ,
,  — энергию.
— энергию.
Энергетический спектр детерминированного сигнала. Обратившись к равенству Парсеваля (1.57), немедленно получаем выражение для энергии сигнала:
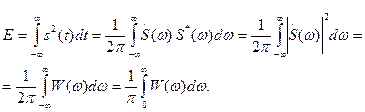 (1.64)
(1.64)
Квадрат модуля спектральной функции
 (1.65)
(1.65)
называют энергетическим спектром сигнала 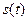 . Энергетический спектр не зависит от фазового спектра сигнала и является вещественной неотрицательной
. Энергетический спектр не зависит от фазового спектра сигнала и является вещественной неотрицательной 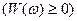 и четной
и четной 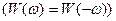 функцией частоты. Размерность энергетического спектра
функцией частоты. Размерность энергетического спектра 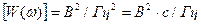 . Энергетический спектр, или «спектральная плотность энергии», описывает распределение энергии сигнала по частоте. Это позволяет, в частности, оценивать долю энергии сигнала, приходящуюся на тот или иной частотный интервал.
. Энергетический спектр, или «спектральная плотность энергии», описывает распределение энергии сигнала по частоте. Это позволяет, в частности, оценивать долю энергии сигнала, приходящуюся на тот или иной частотный интервал.
Пример 1. Полная энергия радиоимпульса (1.15):
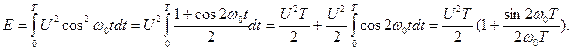
Если длительность радиоимпульса Т много больше периода частоты заполнения То,  , то интеграл
, то интеграл 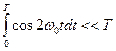 , или, что то же,
, или, что то же, 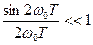 , и полная энергия радиоимпульса
, и полная энергия радиоимпульса 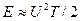 , т. е. в два раза меньше энергии соответствующего видеоимпульса (см. замечание 1 в § 1.5).
, т. е. в два раза меньше энергии соответствующего видеоимпульса (см. замечание 1 в § 1.5).
Удельная мощность непрерывного и периодического сигналов. Определим полную удельную энергию непрерывного сигнала (1.2), существующего при  :
:
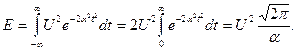
Использован табличный интеграл [4]. Оказывается, модель (1.2) — это модель непрерывного и существующего на бесконечном временном интервале сигнала с ограниченной, конечной энергией. Но чаще встречаются модели неограниченно протяженных во времени (например периодических) сигналов, энергия которых бесконечно велика. Энергетическую оценку моделей таких сигналов проводят, вводя среднюю удельную мощность
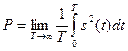 или
или 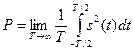
где Т— произвольный временной интервал.
Для периодических сигналов, энергия которых бесконечно велика по определению, усреднение удобно проводить по периоду Т:
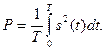 (1.67)
(1.67)
Средняя удельная мощность гармонического сигнала (1.1) 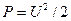 . Применяя формулу (1.67) к периодическому сигналу
. Применяя формулу (1.67) к периодическому сигналу  , представленному в форме (1.16) или (1.19) ряда Фурье, и принимая во внимание условия ортогональности (1.23), для средней мощности Р такого сигнала получим:
, представленному в форме (1.16) или (1.19) ряда Фурье, и принимая во внимание условия ортогональности (1.23), для средней мощности Р такого сигнала получим:
 (1.68)
(1.68)
Полная средняя мощность периодического сигнала равна сумме средних мощностей составляющих сигнал гармоник, включая, естественно, мощность постоянной составляющей («нулевой» гармоники).
Замечание
Иногда используют так называемый односторонний энергетический спектр N(f), аргументом которого выступает линейная частота 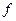 . Односторонний N(f) существует только при
. Односторонний N(f) существует только при 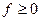 , и вводят его так, чтобы энергия сигнала в полосе частот
, и вводят его так, чтобы энергия сигнала в полосе частот 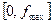 определялась простым соотношением
определялась простым соотношением
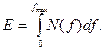
Для определения связи между N(f) и 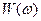 рассмотрим пример: задан сигнал с энергетическим спектром
рассмотрим пример: задан сигнал с энергетическим спектром 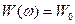 , существующим в интервале круговых частот
, существующим в интервале круговых частот 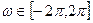 . В соответствии с (1.64) полная (удельная) энергия этого сигнала (Дж)
. В соответствии с (1.64) полная (удельная) энергия этого сигнала (Дж)

Если используется соответствующий односторонний спектр 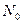 , то
, то
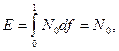
так как  . Следовательно, численная связь между N(f) и
. Следовательно, численная связь между N(f) и 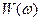 определяется соотношением
определяется соотношением 
Например, если 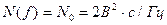 ,то
,то 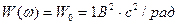 .
.
1.10. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
В теории сигналов наряду со спектральным широко используется корреляционный анализ.
Корреляционная функция (КФ) детерминированного сигнала с ограниченной энергией s(t) определяется выражением
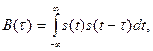 (1.69)
(1.69)
где  — временной сдвиг копии сигнала s(t).
— временной сдвиг копии сигнала s(t).
При вычислении корреляционной (иногда говорят «автокорреляционной») функции финитных сигналов бесконечные пределы интегрирования в (1.69) заменяют на конечные, определяемые интервалом времени, на котором подынтегральная функция  отлична от нуля.
отлична от нуля.
Пример 1. Корреляционная функция прямоугольного видеоимпульса.
На рис. 1.12 показано взаимное расположение сигнала (1.48) и его сдвинутой на время 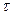 копии
копии 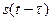 при положительных (рис. 1.12, а) и отрицательных (рис. 1.12, б) значениях
при положительных (рис. 1.12, а) и отрицательных (рис. 1.12, б) значениях  . Область существования отличного от нуля произведения
. Область существования отличного от нуля произведения 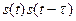 заштрихована.
заштрихована.

Рис. 1.12. Вычисление корреляционной функции прямоугольного видеоимпульса: 
-для 
-для 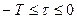
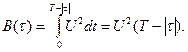
Полученные выражения можно объединить и записать КФ в виде

Аргументом КФ является 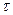 — временной сдвиг копии относительно сигнала s(t); легко видеть, что корреляционная функция сигнала (приведена на рис. 1.13) не зависит от положения s(t) на временной оси: вычисление КФ прямоугольного видеоимпульса (1.4) вновь приведет к результату (1.70).
— временной сдвиг копии относительно сигнала s(t); легко видеть, что корреляционная функция сигнала (приведена на рис. 1.13) не зависит от положения s(t) на временной оси: вычисление КФ прямоугольного видеоимпульса (1.4) вновь приведет к результату (1.70).
Свойства КФ сигналов с ограниченной энергией:
1) 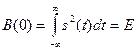 т. е. при
т. е. при 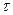 = 0 значение КФ численно равно полной удельной энергии сигнала. Размерность КФ сигнала с конечной энергией
= 0 значение КФ численно равно полной удельной энергии сигнала. Размерность КФ сигнала с конечной энергией 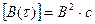 ;
;
2) B(0) 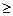 B(t),т. е. КФ имеет максимум при
B(t),т. е. КФ имеет максимум при  = 0 (без доказательства);
= 0 (без доказательства);

Рис. 1.13. Корреляционная функция прямоугольного видеоимпульса
3)  ,т.е. КФ является четной функцией
,т.е. КФ является четной функцией
аргумента 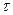 (доказывается заменой переменной);
(доказывается заменой переменной);
4 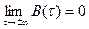 (без доказательства).
(без доказательства).
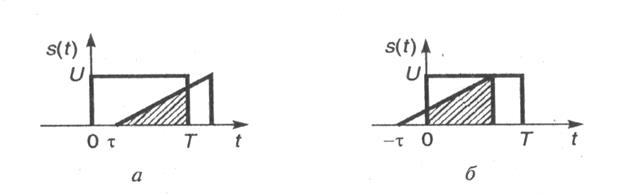
Рис. 1.14. Вычисление ВКФ прямоугольного и треугольного импульсов: 
Взаимная корреляционная функция (ВКФ) сигналов с ограниченной энергией  и
и  определяется выражениями
определяется выражениями
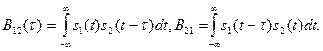 (1.71)
(1.71)
Корреляционная функция является частным случаем взаимной корреляционной функции при 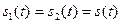 .
.
Пример 2. ВКФ прямоугольного (1.47) и треугольного импульсов. Пусть
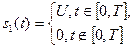 и
и 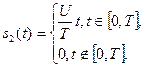
Взаимное расположение сигналов 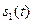 и
и 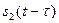 для
для 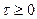 и
и  показано на рис. 1.14, а, б.
показано на рис. 1.14, а, б.
После выполнения соответствующих расчетов получаем следующий результат:
- 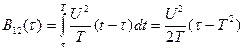 при
при  .
.
- 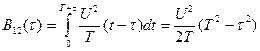 при
при 
График ВКФ прямоугольного и треугольного импульсов приведен на рис. 1.15.
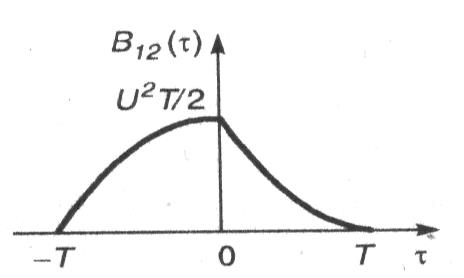
Рис. 1.15. ВКФ прямоугольного и треугольного импульсов
Свойства ВКФ сигналов с ограниченной энергией:
1) 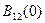 не обязательно является максимальным значением
не обязательно является максимальным значением 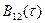 . В качестве при
. В качестве при
мера рекомендуется самостоятельно рассмотреть ВКФ сигналов (1.48) и (1.5);
2)  , где
, где 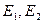 -энергии сигналов
-энергии сигналов 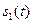 и
и 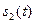 соответственно (без доказательства);
соответственно (без доказательства);
3) при перемене порядка индексации в обозначении ВКФ и соблюдении формы записи, указанной в выражении (1.71), происходит инверсия графика ВКФ относительно оси ординат 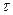 = 0:
= 0:
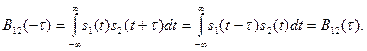
Рекомендуется проверить это положение для сигналов из примера 2 непосредственно;
4) 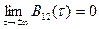 (как и для КФ).
(как и для КФ).
ВКФ является своеобразной мерой «похожести», соответствия, коррелированности двух сигналов при различном их взаимном расположении. КФ отражает корреляцию сигнала с собственной копией; говорят об автокорреляционных свойствах сигнала. Неравенство 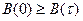 , т. е. непременный максимум КФ при
, т. е. непременный максимум КФ при 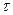 = 0 в этом контексте может трактоваться как свидетельство полной корреляции всякого сигнала с самим собой. Далее, уменьшающиеся (иногда немонотонно) значения
= 0 в этом контексте может трактоваться как свидетельство полной корреляции всякого сигнала с самим собой. Далее, уменьшающиеся (иногда немонотонно) значения 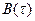 характеризуют меру коррелированности, связи сигнала со своей копией при различных
характеризуют меру коррелированности, связи сигнала со своей копией при различных 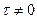 .
.
Корреляционная функция сигналов с неограниченной энергией. Определение (1.69) для вычисления КФ таких сигналов, вообще говоря, не используют по отмечавшимся в § 1.9 причинам (энергия сигнала, т. е. В(0) может оказаться бесконечно большой). КФ непрерывного и периодического сигнала определяют так:

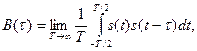 (1.72)
(1.72)
усредняя по интервалу времени 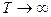 .
.
Пример 3. Корреляционная функция гармонического сигнала (1.1):
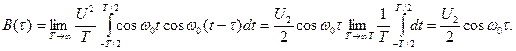
В отличие от КФ и ВКФ финитных сигналов, КФ периодического сигнала сама является периодической функцией и имеет размерность мощности. Значения аргумента 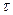 , для которых В(
, для которых В(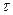 ) = 0, определяют временные сдвиги сигнала и его копии, при которых корреляция отсутствует. Значение B(0) периодического сигнала численно равно мощности сигнала; для гармонического сигнала (1.1)
) = 0, определяют временные сдвиги сигнала и его копии, при которых корреляция отсутствует. Значение B(0) периодического сигнала численно равно мощности сигнала; для гармонического сигнала (1.1) 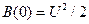 .
.
Замечание 1
Обоснованность требования ограниченности энергии сигналов, КФ и ВКФ которых определяются по соотношениям (1.69) и (1.71), становится очевидным после обсуждения корреляционных свойств моделей сигналов с бесконечно большой энергией. Следует обратить внимание на то обстоятельство, что удовлетворяющие условиям Дирихле (см. § 1.2) финитные сигналы всегда являются сигналами с ограниченной энергией.
Замечание 2
Без доказательства, основываясь на рассмотренных примерах, сформулируем еще одно общее характерное свойство КФ и ВКФ: если исходная (КФ) или одна из исходных (ВКФ) функций не содержит 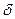 -особенностей, то КФ и ВКФ не содержат скачков (разрывов 1-го рода).
-особенностей, то КФ и ВКФ не содержат скачков (разрывов 1-го рода).
СВЕРТКА СИГНАЛОВ
Свертка сигналов 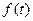 и g(t) определяется интегралом свертки (1.54)
и g(t) определяется интегралом свертки (1.54)
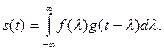
Интеграл свертки используется в теоретической радиотехнике, в частности, для определения сигнала на выходе четырехполюсника. Существуют различные формы представления интеграла свертки; иногда (в литературе по электро- и радиотехнике) интеграл (1.54) называют также интегралом наложения или интегралом Дюамеля. Техника вычисления этого интеграла аналогична технике вычисления КФ и ВКФ (см. § 1.10). Однако следует обратить внимание на весьма существенное различие: переменная, по которой ведется интегрирование, в сомножители подынтегральной функции интеграла (1.54) входит с различными, а интеграла (1.69) — с одинаковыми знаками.
Технику вычисления интеграла свертки удобнее всего пояснять на конкретных примерах.
Пример 1. Возьмем в качестве сигнала f(t) прямоугольный видеоимпульс (1.48), а в качестве сигнала g(t) — финитный сигнал (1.5).
Как следует из выражения (1.54), вычисление интеграла ведется по вспомогательной переменной 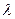 . Аргумент свертки t выступает в качестве параметра. На рис. 1.16, а (в системе координат «
. Аргумент свертки t выступает в качестве параметра. На рис. 1.16, а (в системе координат «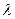 — сигнал») показано взаимное расположение функций, произведение которых образует подынтегральное выражение в (1.54) при t = 0, в частности, инвертированная относительно оси ординат функция
— сигнал») показано взаимное расположение функций, произведение которых образует подынтегральное выражение в (1.54) при t = 0, в частности, инвертированная относительно оси ординат функция
 здесь
здесь 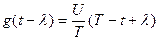 , при t=0 имеем
, при t=0 имеем
 . На рис. 1.16, б показано то же, но для интервала
. На рис. 1.16, б показано то же, но для интервала 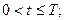
на рис. 1.16, в — для 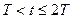 .
.
Интегрирование в (1.54) ведется по интервалу, соответствующему области существования отличного от нуля произведения 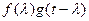 . Именно протяженность и расположение этой области в каждом конкретном случае определяет пределы интегрирования в (1.54). В рассматриваемом случае
. Именно протяженность и расположение этой области в каждом конкретном случае определяет пределы интегрирования в (1.54). В рассматриваемом случае
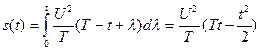 при
при  .
.
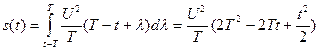 при
при 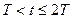 .
.
Рис. 1.16. Вычисление свертки прямоугольного и треугольного импульсов
Рис. 1.17. Свертка прямоугольного и треугольного импульсов
Очевидно, что при t>2T и t<0 свертка s(t) 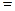 0. График свертки приведен на рис. 1.17. Вычисление свертки ведется по «участкам», что характерно для финитных или кусочно-заданных функций. Если f(t) и g(t) не содержат аддитивно
0. График свертки приведен на рис. 1.17. Вычисление свертки ведется по «участкам», что характерно для финитных или кусочно-заданных функций. Если f(t) и g(t) не содержат аддитивно 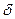 -функций (1.9), то значения свертки в точках соединения (стыках) отдельных участков должны совпадать; в рассматриваемом примере
-функций (1.9), то значения свертки в точках соединения (стыках) отдельных участков должны совпадать; в рассматриваемом примере
s(T)= U2 Т/2.
Читателю рекомендуется сравнить полученный здесь результат и
результат вычисления ВКФ (см. пример 2 § 1.10). Заменой переменной показывают (это предоставляется читателю сделать самостоятельно), что интеграл (1.54) можно также записать в виде
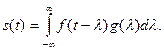 (1.74)
(1.74)
Результаты вычислений по формулам (1.54) и (1.74) совпадают; выбор той или иной формы записи определяется соображениями упрощения вычислений.
Разумеется, можно вычислять свертку не только финитных функций, но и функций, определенных на любых, в том числе бесконечных, интервалах.
Пример 2. В качестве сигнала f(t) вновь возьмем прямоугольный видеоимпульс (1.48), а в качестве сигнала g(t) — экспоненту (1.3).
Рисунок, отражающий взаимное положение функций 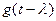 и
и 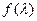 в системе координат «
в системе координат « сигнал», читателю предлагается выполнить самостоятельно. Интеграл свертки записывается следующим образом:
сигнал», читателю предлагается выполнить самостоятельно. Интеграл свертки записывается следующим образом:
 при
при 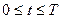 .
.
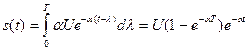 при
при 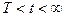 .
.
При t<0 свертка s(t) 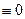 .
.
Пример 3. Рассмотрим, наконец, свертку произвольного сигнала  с функцией Дирака
с функцией Дирака  . Согласно формулам (1.54) и (1.74) с учетом фильтрующего свойства (1.11)
. Согласно формулам (1.54) и (1.74) с учетом фильтрующего свойства (1.11) 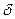 -функции, можем записать
-функции, можем записать
 .
.
Пример 3. Рассмотрим, наконец, свертку произвольного сигнала 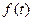 с функцией Дирака
с функцией Дирака  Согласно формулам (1.54) и (1.74) с учетом фильтрующего свойства (1.11)
Согласно формулам (1.54) и (1.74) с учетом фильтрующего свойства (1.11) 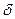 -функции, можем записать
-функции, можем записать
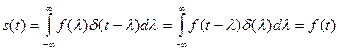
Сверткой произвольной функции с функцией Дирака является сама произвольная функция.
1.12. КОРРЕЛЯЦИОННО-СПЕКТРАЛЬНЫЙ АНАЛИЗ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
Особенно важным вопросом является связь корреляционных и спектральных характеристик детерминированных сигналов.
Корреляционная функция и энергетический спектр. Поставим в соответствие сигналам 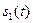 и
и 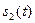 спектральные функции
спектральные функции  и
и 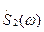 . Обратимся к определению ВКФ (1.71) и, последовательно воспользовавшись теоремой о спектре сдвинутого во времени сигнала (1.47) и теоремой Рэлея (1.56), представим
. Обратимся к определению ВКФ (1.71) и, последовательно воспользовавшись теоремой о спектре сдвинутого во времени сигнала (1.47) и теоремой Рэлея (1.56), представим
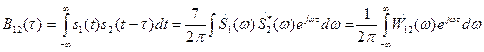
Комплексная в общем случае функция
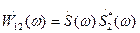 (1.76)
(1.76)
называется взаимным энергетическим спектром сигналов 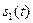 и
и 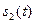 Но выражение (1.75) является обратным преобразованием Фурье (1.32) с ядром
Но выражение (1.75) является обратным преобразованием Фурье (1.32) с ядром 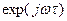 , примененным к взаимному энергетическому спектру
, примененным к взаимному энергетическому спектру 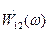 ; следовательно, существует соответствующее прямое преобразование Фурье:
; следовательно, существует соответствующее прямое преобразование Фурье:
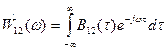 (1.77)
(1.77)
Соотношения (1.75) — (1.77) являются основой корреляционно-спектрального анализа детерминированных сигналов. В частности, определение (1.75) позволяет глубже осмыслить уже обсуждавшееся понятие ВКФ. В самом деле, при неперекрывающихся (концентрирующихся в различных частотных интервалах) спектрах 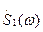 и
и 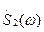 произведение
произведение  . Следовательно и
. Следовательно и 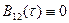 , т. е. эти сигналы оказываются абсолютно некоррелированными.
, т. е. эти сигналы оказываются абсолютно некоррелированными.
Положив в (1.75) 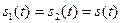 получим соотношения, связывающие КФ сигнала с его энергетическим спектром
получим соотношения, связывающие КФ сигнала с его энергетическим спектром
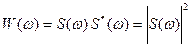 , введенным выражением (1.64):
, введенным выражением (1.64):
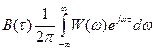 ,
, 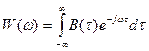 (1.78)
(1.78)
Замечание
В(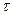 ), как и
), как и 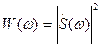 , не зависит от фазовой спектральной функции сигнала s(t). Но форма сигнала s(t) при заданной спектральной функции амплитуд
, не зависит от фазовой спектральной функции сигнала s(t). Но форма сигнала s(t) при заданной спектральной функции амплитуд 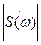 существенно
существенно
зависит от фазового спектра  ; поэтому можно утверждать, что различные по форме, но обладающие одинаковыми амплитудными спектрами сигналы имеют одинаковые КФ.
; поэтому можно утверждать, что различные по форме, но обладающие одинаковыми амплитудными спектрами сигналы имеют одинаковые КФ.

 2020-04-20
2020-04-20 3234
3234