Способы задания множеств

1 2 3 4 5

Лекция 1. Теория множеств

План лекции

1.1. Понятие множества

1.2. Способы задания множеств

1.3. Сравнение множеств

1.4. Операции над множествами.

1.4.1. Основные операции над множествами

1.4.2. Свойства операций над множествами

1.4.3. Декартовое произведение множеств

1.5. Счетные и несчетные множества

Понятие множества

Понятие «множество», как и любое другое исходное понятие математической теории не является строго определяемым. Его синонимами являются «совокупность», «семейство», «класс», «система», «собрание», «ансамбль», «коллекция» и др.

Например, Кантор, основатель теории множеств, дал такое определение: «под множеством понимают объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью».

Примеры множеств:

множество столов в комнате;

множество всех рыб в океане;

множество всех футбольных команд

В математике рассматриваются:

множество точек (например, окружности),

множество чисел (например, действительных),

множество всех решений уравнения sinx=0,5,

множество всех чисел вида .

Определение. Предметы (объекты), составляющие данное множество, называют его элементами.

При этом никаких ограничений на природу элементов множества не накладывается. Предполагается только, что для любых двух элементов данного множества имеется возможность выяснить, различны они или одинаковы.

Тот факт, что элемент x принадлежит множеству А (x является элементом множества А), записывается так: . Если же x не является элементом множества А (x не принадлежит множеству А), то пишут . Таким образом, принадлежность – это отношение между элементами и множествами, при этом предполагается, что для любого конкретного элемента и любого конкретного множества можно определить, принадлежит этот элемент данному множеству или нет.

Понятие множества – одно из основных понятий современной математики. Понятия и теоремы теории множеств обладают большой общностью, так как элементы множеств могут быть различной природы, а потому одни и те же утверждения, касающиеся множеств, можно истолковать как утверждения о точках, натуральных числах, молекулах и т.д.

Определение. Множество, элементами которого являются другие множества, называется классом или семейством.

В классе все элементы имеют различную природу образования, но у них есть хотя бы одно общее свойство.

ПРИМЕР. Семейство АУДИТОРИЯ имеет следующие элементы:

Множество парт

Множество ламп

Множество элементов питания

Множество студентов и т.д.

Определение. Множество называется конечным, если оно состоит из конечного числа элементов, и бесконечным – в противоположном случае.

Рисунок 1.1 – Виды множеств

Определение. Количество элементов в конечном множестве называется его мощностью и обозначается | А |. Также мощность называется кардинальным числом множества. Другими словами, это характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.

Определение. Множество нулевой мощности, не содержащее элементов, называется пустым и обозначается Æ.

Оно введено для удобства: лучше сказать, что множество пусто, чем объявить его несуществующим. В нашем примере множество студентов в аудитории может быть пустым.

Определение. Множества, имеющие одинаковое количество элементов, называются равномощными.

Определение. Класс всех рассматриваемых множеств называется универсальным множеством или универсумом (обозначается).

ПРИМЕР. Множество планет Солнечной системы U = {Земля, Марс, Венера, Юпитер, Сатурн, Уран, Плутон, Меркурий, Нептун}.

Элементы множества не могут повторяться: А={1,2,1,4,6} не является описанием множества. Сразу возникает вопрос о способах описания (задания) множества.

Способы задания множеств.

Диаграммы Эйлера-Венна. Это графическое изображение множеств в универсуме. Универсум изображается прямоугольником, внутри которого располагаются множества, иллюстрирующиеся овалами. Результирующее множество выделяется штриховкой.

Рисунок 1.2 – Диаграмма Эйлера-Венна

Перечисление элементов. А={а₁ а₂ а₃ а₄ а₅ а₆}. Списком можно задавать только конечные множества. В данном случае последовательность элементов множества в произвольном порядке записывается в фигурных скобках. Множество целых чисел от n до m обозначается А_n_.._m

ПРИМЕР. D _{-3.. 3} ={ -3, -2, -1, 0, 1, 2, 3}

Характеристический предикат. Это задание с помощью характеристического предиката множества А, т.е. такого свойства, которым обладают все элементы множества А и не обладают элементы, не принадлежащие А. Если Р (x) – некоторое свойство, то предполагается, что оно определяет некоторое множество А, состоящее из всех тех элементов x, которые удовлетворяют свойству Р (x).Вэтом случае множество А обозначают так: A = { x | P (x)} или A = { x: P (x)}. Например, если А = { a ₁, …, a_n }, то оно может быть определено с помощью характеристического свойства следующим образом: A = { x | x = a ₁ или x = a ₂, или … или x = a_n }.

ПРИМЕР. D ={nÎZ| -4<n<4}

Такие задания могут приводить к противоречиям, таким как парадокс Рассела: класс всех множеств, не содержащих себя в качестве элемента: А ={ B | B Ï B }. Имеем: А Î А, тогда А Ï А и обратно: А Ï А, тогда А Î А. (Задача о лгунах: я всегда вру.)

Порождающая процедура. Порождающая процедура описывает способ получения элементов множества из уже полученных элементов либо из других объектов. Элементами множества считаются все объекты, которые могут быть построены с помощью такой процедуры. А ={ х | х = F }. Здесь F – процедура, при работе которой появляются элементы множества.

ПРИМЕР. А ={1, 2, 4, 8, 16, …}={ n | 1Î A Ù(n Î A Þ2 n Î A)}

Такое задание также называется рекурсивным. В курсе общей математики способ носит название математической индукции.

Сравнение множеств

Определение. Пусть А и В – непустые множества. Если каждый элемент множества А является вместе с тем и элементом множества В, то А называют подмножеством множества В (или А содержится в В,или В содержит А, или А включено в В) и обозначают . То есть " х Î А Þ х Î В.

Множество В называется покрывающим множество А.

Положим, по определению, что пустое множество есть подмножество любого множества В, в том числе и пустого.

ПРИМЕР. Пусть С – множество всех комплексных чисел; R – множество всех действительных чисел; Q – множество всех рациональных чисел; Z – множество всех целых чисел; N – множество всех натуральных чисел. Тогда, .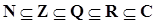

Определение. Булеан (степень множества, показательное множество, множество частей) – множество всех подмножеств данного множества A, и обозначается P (A) или 2 ^A.

Понятие подмножества определяет отношение между двумя множествами – отношение включения. Отметим простейшие свойства введенного отношения включения:

1) , т. е. любое множество А является подмножеством самого себя;

2) если , , то .

Чтобы в множестве А выделить подмножество В, добавляют к характеристическому признаку множества А то или иное дополнительное свойство Р (х) и обозначают это так: B = { | P (x)}.

ПРИМЕР. { | x >0} –множество всех положительных действительных чисел.

Введем наряду с отношением включения множеств еще одно отношение – отношение равенства множеств.

Определение. Пусть А и В – два множества. Множества А и В называются равными, если каждый элемент множества А является вместе с тем и элементом множества В, и обратно, каждый элемент множества В является и элементом множества А. Другими словами, множества А и В называются равными, если выполняются два включения: 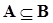и .

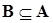Отношение равенства двух множеств, очевидно, удовлетворяет следующим условиям:

1) А = А;

2) если А = В и В = С, то А = С.

Определение. Есл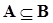и и , то А называют собственным подмножеством множества В и обозначают . Введенное отношение называется отношением строгого включения.