1) Так как декартовы произведения А ´ B и В ´ А состоят из различных элементов, то операция нахождения декартова произведения множеств свойством коммутативности не обладает.
2) Аналогично рассуждая, можно доказать, что для этой операции не выполняется и свойство ассоциативности.
3) Но она дистрибутивна относительно объединения и разности множеств, т.е. для любых множеств А, В и С выполняются равенства:
(A È B) ´ С = (A ´ С) È (B ´ С), (A \ B) ´ С = (A ´ С) \ (B ´ С).
ПРИМЕР. Проверьте справедливость свойства дистрибутивности декартова произведения относительно объединения, если: А = {3; 4; 5},
В = {5; 7}, С = {7; 8}.
РЕШЕНИЕ. Найдем объединение множеств А и В: A È B = {3; 4; 5;7}. Далее перечислим элементы множества (A È B)´ С, используя определение операции декартова произведения множеств: (A È B)´ С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.
Чтобы найти элементы множества (A ´ С) È (B ´ С), перечислим сначала элементы множеств А ´ С и В ´ С:
А ´ С = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8)}
В ´ С = {(5; 7), (5; 8), (7; 7), (7; 8)}.
Найдем объединение полученных декартовых произведений:
(A ´ С) È (B ´ С) = {(3; 7), (3; 8), (4; 7), (4; 8), (5; 7), (5; 8), (7; 7), (7; 8)}.
Видим, что множества (A È B) ´ С и (A ´ С) È (B ´ С) состоят из одних и тех же элементов, следовательно, для данных множеств А, В и С справедливо равенство (A È B) ´ С = (A ´ С) È (B ´ С).
Выясним теперь, как можно наглядно представить декартово произведение множеств.
Если множества А и В конечны и содержат небольшое число элементов, то можно изобразить декартово произведение этих множеств при помощи таблицы или графически.
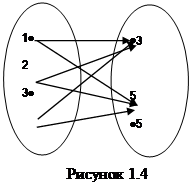
ПРИМЕР. Декартово произведение множеств А = {1; 2; 3} и В = {3; 5} можно представить так, как показано на рисунке 1.3 и 1.4
| 3 | 5 |
| 1 | (1,3) | (1,5) |
| 2 | (2,3) | (2,3) |
| 3 | (3,3) | (3,3) |
Рисунок 1.3
 2020-04-20
2020-04-20 366
366








