Построение доверительного интервала для параметра закона Пуассона

Рассмотрим построение доверительного интервала для параметра λ распределения Пуассона. В экспериментальной ядерной физике очень часто приходится довольствоваться одним наблюдением пуассоновской случайной величины – числом зарегистрированных за некоторое время отсчетов k_e. Нужно найти два числа k₂> k_e и k₂< k_e в качестве границ доверительного интервала так, чтобы приняв в качестве оценки параметра λ величину k₂ вероятность получить значение меньше k_e не превышала , где - доверительная вероятность, а приняв в качестве λвеличину k₁, вероятность получить значение больше k_e тоже не превышала (рис. 1):

Рис. 1. Построение доверительного интервала

Тем самым будет установлено, что

Граничные числа k₁ и k₂ находятся как решения приведенных уравнений. Эти числа могут быть выражены через процентные точки распределения :

Очевидно, что границы доверительного интервала не симметричны относительно , что следует из асимметрии распределения Пуассона.

Имеются таблицы для нахождения границ доверительных интервалов для различных значений оценки параметра распределения Пуассона λ. Ниже приведены значения доверительных границ для доверительной вероятности 1-α = 0,95.

k_e	0	1	2	3	4	5	6	7	8	9	10	11
k₁	0	0,025	0,242	0,619	1,09	1,62	2,20	2,81	3,45	4,02	4,79	5,44
k₂	3,69	5,57	7,23	8,77	10,24	11,67	13,06	14,42	15,82	15,76	18,42	19,73

12	13	14	15	16	17	18	19	20	21	22	23	24
6,23	6,91	7,73	8,42	9,43	9,92	10,71	11,52	12,21	13,0	13,81	14,62	15,43
21,02	23,31	23,51	24,81	26,03	27,21	28,42	27,61	30,79	32,01	33,19	34,41	35.62

На первый взгляд вызывает удивление существование верхней границы при . Однако следует отдавать себе отчет в том, что отсутствие отсчетов за промежуток времени регистрации еще не гарантирует их отсутствие при большем времени наблюдения. Разумеется, верхнее значение доверительного интервала растет с увеличением .

Доверительные границы для интенсивности потока равны:

где Т – время регистрации отсчетов.

При λ>15 распределение Пуассона достаточно хорошо аппроксимируется нормальным распределением. Например, зарегистрировано =20 событий. Точные оценки через распределение доверительного интервала =0,95 =12,22 и =30,89, а оценки через квантили нормального распределения -1,96 и 1,96 дают =11,2 и =28,8. Поэтому в экспериментальной работе для предварительной оценки погрешности числа отсчетов за одно измерение часто используют значения ; 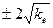и соответственно для доверительных вероятностей 0,68; 0,95 и 0,998, если, конечно, есть уверенность в отсутствии помех.