Замечания.
1). Если 
2). Если в задаче требуется найти тангенс угла, то можно найти косинус угла, затем синус угла (по основному тождеству) и вычисляем тангенс.


1. 
Что бы найти угол между прямыми АВ и РК, надо выбрать направляющие вектора  и
и  , задать их координаты по формуле
, задать их координаты по формуле




 найти угол между векторами
найти угол между векторами  и
и  по формуле
по формуле



 Угол между прямыми всегда острый и косинус угла между ними всегда положительный. Поэтому косинус угла между прямыми равен модулю косинуса угла между векторами
Угол между прямыми всегда острый и косинус угла между ними всегда положительный. Поэтому косинус угла между прямыми равен модулю косинуса угла между векторами
 =
= 
2.Нахождение угла между прямой и плоскостью
Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость. Нормаль – это вектор перпендикулярный к данной плоскости -  .
.
Что бы найти угол между прямой АВ и плоскостью  , надо задать направляющий вектор
, надо задать направляющий вектор  и вектор
и вектор 
 , перпендикулярный к плоскости
, перпендикулярный к плоскости 
 BH – перпендикуляр к плоскости
BH – перпендикуляр к плоскости 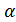 ,
,
АВ – наклонная, АH – проекция АВ на плоскость  ,
,
 угол между прямой АВ и плоскостью
угол между прямой АВ и плоскостью 
 угол между прямой АВ и перпендикуляром BH
угол между прямой АВ и перпендикуляром BH


Синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором и нормалью к плоскости.

 Пусть
Пусть  и
и 


 Находим
Находим 
 будет равен модулю этого выражения (без знака минус)
будет равен модулю этого выражения (без знака минус)
3. Нахождение угла между плоскостями.
Чтобы найти угол между плоскостями при помощи метода координат, надо найти угол между двумя нормалями к этим плоскостям.
Пусть надо найти угол между плоскостями  .
.

 Вектор
Вектор 


Как определить координаты нормали(перпендикуляра)к плоскости.
Если прямая перпендикулярна плоскости, то она перпендикулярна двум пересекающимся прямым, лежащих в этой плоскости.
 и
и  –два направляющих вектора, лежащих в плоскости
–два направляющих вектора, лежащих в плоскости  ,
,
 плоскости
плоскости  ,
,
 числа,
числа,  – неизвестные.
– неизвестные.
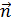


B 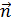
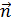

 и
и 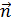




A C 
Что бы решить систему двух уравнений с тремя неизвестными, надо выразить два неизвестных через третье и подставляем произвольное значение этого неизвестного в два других.
Пример решения задач методом нормалей
Дан куб. Точка Е- середина  . Найти угол между плоскостями AEF и BC
. Найти угол между плоскостями AEF и BC 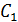 .
.
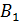
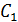
E 
 BC
BC 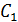
 F
F 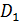
 AEF,
AEF, 







B C 

A D 



Выражаем x и y через z 


 Пусть z=1, тогда
Пусть z=1, тогда 

 и
и 
 =
= 
 =
= 

Тренажер 2.3.1. Решение задач с помощью метода координат
1. В кубе 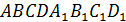 найти косинус угла между прямыми AE и BF, если точка E –середина
найти косинус угла между прямыми AE и BF, если точка E –середина  F – середина
F – середина 
2. В правильной треугольной призме  все ребра равны. Найти косинус угла между прямыми AВ и
все ребра равны. Найти косинус угла между прямыми AВ и 
3. В правильной шестиугольной призме  все ребра равны. Найти косинус угла между прямыми A
все ребра равны. Найти косинус угла между прямыми A 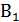 и
и 
4. В правильной треугольной пирамиде SABC все ребра равны.  M – середина АС,
M – середина АС,  N – середина СВ. Найти угол между прямыми AN и
N – середина СВ. Найти угол между прямыми AN и 
5. В правильной четырехугольной пирамиде SABC  все ребра равны.
все ребра равны.
 Е – середина SB,
Е – середина SB,  F – середина SС. Найти угол между прямыми AE
F – середина SС. Найти угол между прямыми AE
и 
6. В кубе 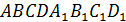
 Е – середина
Е – середина  Найти синус угла между прямой АЕ и плоскостью В
Найти синус угла между прямой АЕ и плоскостью В  .
.
7. В прямоугольном параллелепипеде 
 Е – середина АВ и
Е – середина АВ и
 – середина
– середина  А
А  Найти тангенс угла
Найти тангенс угла
между прямой Е  и плоскостью А
и плоскостью А  .
.
8. В правильной шестиугольной призме  все ребра равны.
все ребра равны. 
 – середина
– середина  . Найти синус угла между прямой АК и плоскостью В
. Найти синус угла между прямой АК и плоскостью В  .
.
9. В правильной шестиугольной пирамиде  сторона основания равна 1, а боковое ребро равно 2. Найти синус угла между прямой АС и плоскостью А
сторона основания равна 1, а боковое ребро равно 2. Найти синус угла между прямой АС и плоскостью А  .
.
10. В кубе 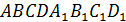
 E –середина
E –середина  F – середина
F – середина 
Найти тангенс угла между плоскостями  и
и 
11. В прямоугольном параллелепипеде  А
А 
 Найти косинус угла между плоскостями С
Найти косинус угла между плоскостями С  В
В  .
.
12. В кубе 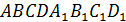
 E – середина
E – середина 
 F - середина
F - середина  Найти угол между плоскостями
Найти угол между плоскостями  и
и 
Справочный материал.
Основные формулы планиметрии
Треугольник

Прямоугольник Параллелограмм 


Ромб

Трапеция


Круг и его части
Большой и маленький радиусы



Правильные многоугольники
Треугольник Квадрат Шестиугольник







 2020-04-20
2020-04-20 139
139








