1. Расстояние между прямым и –
а) длина их общего перпендикуляра.
A
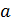
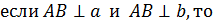
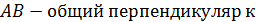
прямым 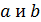 .
.
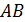 – расстояние между прямыми
– расстояние между прямыми 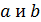
 B
B 
б). длина перпендикуляра, опущенного из точки, лежащей на одной прямой до плоскости, которая параллельна этой прямой, и в которой лежит вторая прямая (т.е. находим расстояние от точки до плоскости методом объемов)
 ,
,



Расстояние от точки до прямой – длина перпендикуляра, опущенного из точки на прямую.
если 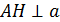 , то
, то  -расстояние от точки А
-расстояние от точки А
А до прямой 
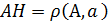
H
Метод площадей: составить площадь треугольника двумя разными способами.
Что бы найти расстояние от точки до прямой надо на прямой выбрать две точки и получить треугольник, в котором искомый перпендикуляр будет высотой. Найти площадь этого треугольника любым возможным способом и из формулы 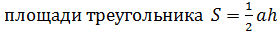 найти искомое
найти искомое 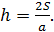
Треугольник может быть равносторонний 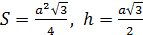
прямоугольный 
 равнобедренный
равнобедренный 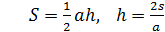
разносторонний  ,
, 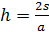
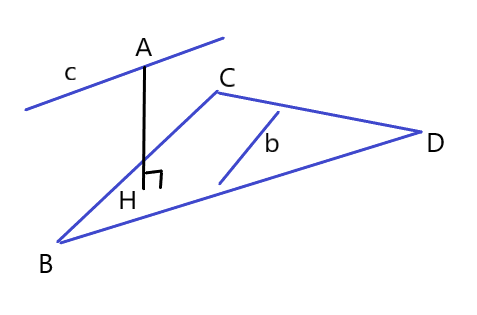
Пример. В правильной треугольной призме все ребра равны 1. Найти расстояние от точки А до прямой 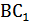
 Рассмотрим
Рассмотрим 
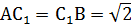 ,
, 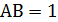
1  H Проведем высоту
H Проведем высоту 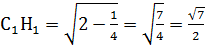
 (
( =
= 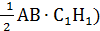
A  B
B  (
( =
= 
1 C 
Ответ: 
2. Расстояние от точки до плоскости – это длина перпендикуляра, опущенный из точки на плоскость.
А
если 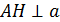 , то
, то  -расстояние от точки А
-расстояние от точки А
 до плоскости
до плоскости 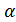
H 
Метод объемов: составить объем пирамиды двумя разными способами.
Что бы найти расстояние от точки до плоскости, надо на плоскости выбрать три точки и получить пирамиду, в котором искомый перпендикуляр будет высотой. Найти объем этой пирамиды любым возможным способом и из формулы  найти искомое
найти искомое 
Пример. В правильной четырехугольной пирамиде SABCD все ребра равны по 1. Н 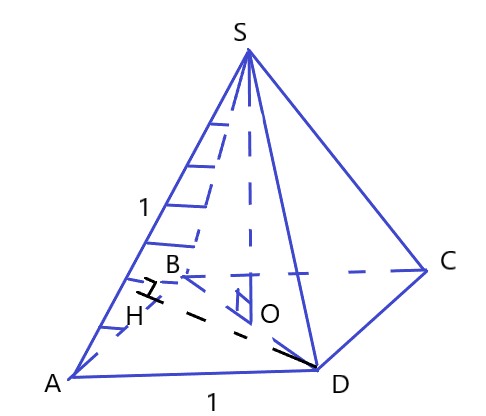 айти расстояние от вершины D до плоскости SA
айти расстояние от вершины D до плоскости SA
 .
.


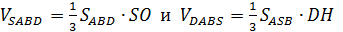
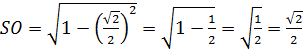
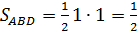
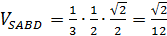

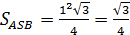




Ответ: 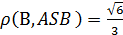
Тренажер 1.5.1. Расстояние между фигурами.
1. В кубе  .найти расстояние от точки В до прямой D
.найти расстояние от точки В до прямой D 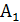
2. В правильной треугольной призме ABC  все ребра равны 1. Найти расстояние от точки В до прямой А
все ребра равны 1. Найти расстояние от точки В до прямой А  .
.
3. В правильной шестиугольной пирамиде  сторона основания равна 1, а боковое ребро равно 2. Найти расстояние от точки В до прямой
сторона основания равна 1, а боковое ребро равно 2. Найти расстояние от точки В до прямой 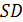 .
.
4. В правильной шестиугольной призме  все ребра равны 1. Найти расстояние от точки В до прямой
все ребра равны 1. Найти расстояние от точки В до прямой  .
.
5. В правильной шестиугольной призме  все ребра равны 1. Найти расстояние от точки В до прямой
все ребра равны 1. Найти расстояние от точки В до прямой 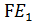 .
.
6. В кубе  найти расстояние от точки
найти расстояние от точки 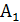 до плоскости
до плоскости 
7. В правильной шестиугольной пирамиде  сторона основания равна 1, а боковое ребро равно 2. Найти расстояние от точки А до плоскости SDE.
сторона основания равна 1, а боковое ребро равно 2. Найти расстояние от точки А до плоскости SDE.
8. В правильной шестиугольной пирамиде  сторона основания равна 1, а боковое ребро равно 2. Найти расстояние между прямыми SB и AF.
сторона основания равна 1, а боковое ребро равно 2. Найти расстояние между прямыми SB и AF.
9. В правильной четырехугольной пирамиде  все стороны равны 1. Найти расстояние между прямыми
все стороны равны 1. Найти расстояние между прямыми 
10. В правильной шестиугольной призме  все ребра равны 1. Найти расстояние между прямыми
все ребра равны 1. Найти расстояние между прямыми 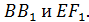
Тема 1.6. Практическая стереометрия
1). Площади поверхности и объемы подобных тел.

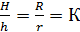
 конусы подобны
конусы подобны
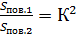
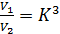
2). Зависимость площади поверхности и объема от стороны или радиуса
В сфере:
если радиус сферы увеличивается в К раз, то площадь поверхности сферы увеличивается в К2 раза, а объем (вес) увеличивается в К3 раз.
В правильном тетраэдре и кубе:
если сторона увеличивается в К раз, то площадь боковой и полной поверхности увеличивается в К2 раза, объем (вес) увеличивается в К3раз
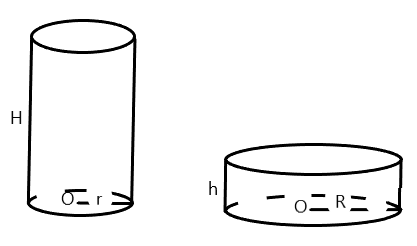
3). Воду переливают из одного цилиндрического сосуда в другой.
Если при постоянном объеме жидкости радиус основания цилиндра увеличивается в К раз, то площадь основания цилиндра  увеличивается в К2 раза, при этом высота должна уменьшится тоже в
увеличивается в К2 раза, при этом высота должна уменьшится тоже в 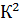 раза
раза

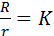

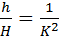
4). Зависимость площади поверхности конуса и цилиндра от радиуса основания и высоты
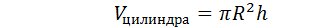
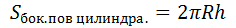


Площадь боковой поверхности от всех элементов зависит линейно, а объем от высоты зависит линейно, а от радиуса квадратично
В цилиндре и конусе при увеличении (или уменьшении) радиуса основания, или высоты, или образующей в  раз площадь боковой поверхности увеличивается (или уменьшается)в
раз площадь боковой поверхности увеличивается (или уменьшается)в  раз.
раз.
При увеличении (или уменьшении) высоты в К раз объем увеличивается (или уменьшается) в К раз, а при увеличении (или уменьшении) радиуса основания в К раз объем увеличивается (или уменьшается) в  раз.
раз.
Пример. Объем цилиндре равен 12, а площадь боковой поверхности равна 9 Радиус основания увеличили в 2 раза, а высоту уменьшили в 3 раза. Найти объем и площадь боковой поверхности получившегося цилиндра.

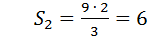
5). Объемы цилиндра и конуса, имеющих одинаковые радиусы основания и высоты.

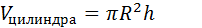



6). Объем детали, опущенной в воду равен объему вытесненной жидкости

 - первоначальный объем воды
- первоначальный объем воды
 - объем вытесненной жидкости (объем детали)
- объем вытесненной жидкости (объем детали)
1 способ




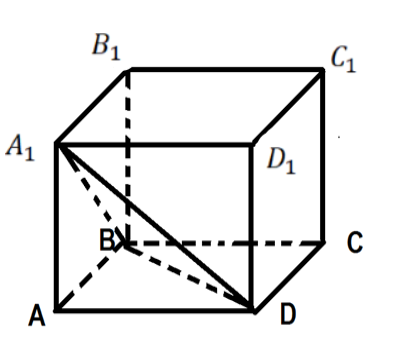
7 ). Объемы частей призмы
Сравнить объемы призмы 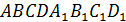 и пирамиды
и пирамиды 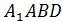 , осекаемой от призмы плоскостью, проходящей через точки
, осекаемой от призмы плоскостью, проходящей через точки 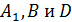


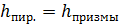
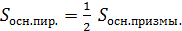
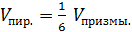
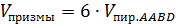
 2020-04-20
2020-04-20 205
205








