Динамических характеристик САР

Динамические характеристики САР определяются при стандартных входных воздействиях. В теории автоматического регулирования в качестве стандартных воздействий приняты: ступенчатая функция Хевисайда х_вх(t)=A_вх[1(t)]; дельта-функция х_вх(t)=d(t) или функция Дирака; гармоническая функция х_вх(t)=А_вхsin wt, где  А_вх  - величина ступени (или амплитуда) входного воздействия; w - угловая частота колебаний, t - время. В практике исследований САР наибольшее распространение получили ступенчатая и гармоническая функции. При задании гармонического входного сигнала анализируются частотные характеристики САР, а при ступенчатом - устойчивость и качество регулирования САР.

При исследовании динамических характеристик САР обычно считаются заданными: принципиальная схема САР, включающая объект регулирования и регулятор с указанием регулируемого параметра и регулирующего фактора, управляющего и возмущающего воздействия, а также числовые значения параметров САР.

Исследование САР начинается с описания назначения и принципа действия системы с четким выделением объекта регулирования и характерных элементов регулятора: чувствительного элемента; задающего устройства; элементов сравнения; усилителя; исполнительного механизма; корректирующего элемента. Рассматривается состояние системы при установившемся режиме работы и в динамике при управляющем и возмущающем воздействиях.

Выделяются типовые звенья САР и для них выводятся дифференциальные уравнения. Типовым звеном представляется, как правило, объект регулирования и каждый характерный элемент регулятора. Вывод уравнения звена начинается с определения координат и выбора направления их отсчета. За положительные направления отсчета принимают такие, при движении по которым происходит процесс компенсации отклонения регулируемого параметра при действии возмущений или процесс установления нового его значения в соответствии с управляющим воздействием. Положительные направления перемещений элементов на схеме обозначают стрелками.

Для каждого из выделенных элементов принимаются упрощающие допущения и на основе законов физики, механики, гидрогазодинамики записываются соответствующие уравнения. Например, для подвижных элементов записывается уравнение движения, а для элементов, связанных с протоком жидкости, - уравнение расходной характеристики и баланса расходов. Если в выражение входят нелинейные зависимости, то производится их линеаризация путем разложения функций в ряд Тейлора около точки, соответствующей равновесному (установившемуся) режиму, с учетом первых двух членов разложения. Вводятся базисные величины, за которые обычно принимают значения параметров при данном установившемся режиме, и записываются уравнения звеньев в относительных координатах. Полученные уравнения звеньев сводят в систему уравнений и проверяют их “замкнутость”. Число переменных в уравнениях (исключая управляющие и возмущающие воздействия) должно быть равно числу уравнений.

При наличии системы дифференциальных уравнений исследование динамических характеристик САР может быть выполнено различными методами. В теории автоматического регулирования наибольшее распространение получил операторный метод, основанный на преобразовании Лапласа [2, 3].

Система дифференциальных уравнений представляется в операторной форме и для каждого из выделенных звеньев записывается передаточная функция 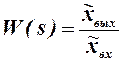 как отношение выходного параметра ко входному в изображениях по Лапласу при нулевых начальных условиях. Для этого в дифференциальных уравнениях производится замена  а сами переменные записываются в изображениях по Лапласу: 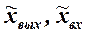. Например, для турбореактивного двигателя (ТРД) как объекта регулирования, описывающего дифференциальным уравнением

,

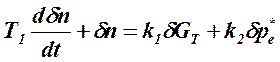операторное уравнение имеет вид

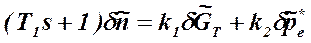                 (1.1)

где 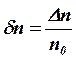, , 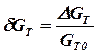 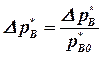- относительные приращения частоты вращения ротора двигателя, расхода топлива и давления заторможенного потока воздуха на входе в двигатель соответственно; Т₁ - постоянная времени ТРД; k₁ , k₂ - коэффициенты передачи по соответствующим воздействиям. Уравнение (1.1) может быть выражено через передаточные функции в виде

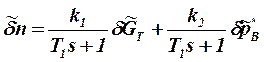
или

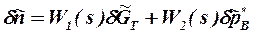                         (1.2)

 

где 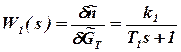 - передаточная функция ТРД по регулирующему воздействию (при );

 - передаточная функция ТРД по возмущающему воздействию (при ).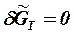

Для получения компактных структурных схем иногда целесообразно уравнение (1.2) представить в форме

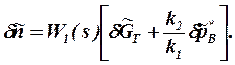                          (1.3)

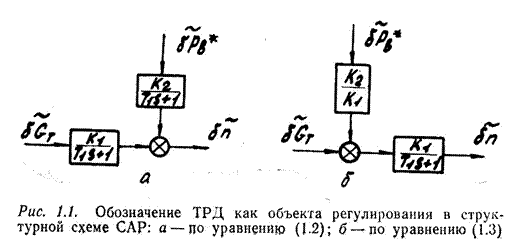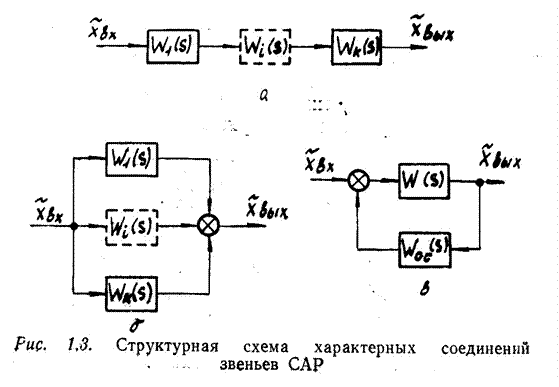
Составляется структурная схема САР. Для этого каждое звено обозначается в виде прямоугольника, внутри которого записывается выражение для передаточной функции; входной и выходной параметры обозначаются входящими и выходящими стрелками (рис. 1.1). Затем звенья соединяются в соответствии с системой уравнений и правилами построения структурных схем. При этом четко выделяются: регулируемый параметр; управляющие и возмущающее воздействия; обратные связи. Структурные схемы отражают направления воздействий одного звена на другое, которые не всегда согласуются с направлениями физических параметров на принципиальных схемах, например, с направлением потока жидкости в элементах САР.

 

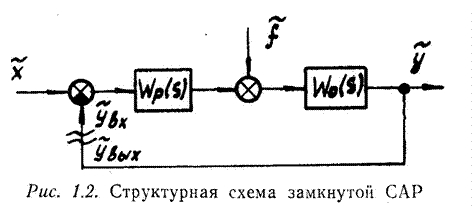
Определяются характерные передаточные функции САР. Структурная схема САР условно размыкается между объектом регулирования и чувствительным элементов (рис. 1.2) Вводятся

обозначения 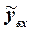- отклонение регулируемого параметра на входе в чувствительный элемент, а  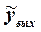- отклонение регулируемого параметра на выходе из объекта регулирования. Определяется передаточная функциясистемы в разомкнутом состоянии: 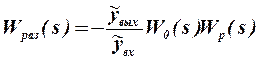. При этом в структурной схеме выделяются группы характерных соединений звеньев, которые заменяют эквивалентным звеном с передаточной функцией:

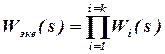 - при последовательном соединении звеньев (рис. 1.3,а);

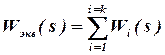 - при параллельном согласном соединении звеньев (рис. 1.3,б);

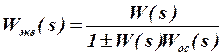 - для звеньев, охваченных обратной связью (рис. 1.3,в), причем знак ”+” - для отрицательной, а знак “-“ для

положительной обратной связи. Для систем со сложной схемой используются специальные правила преобразования структурных схем [2, 3, 4].

Передаточная функция замкнутой системыопределяется, как и передаточная функция системы в разомкнутом состоянии, нахождением передаточных функций характерных соединений и применением правил преобразования структурных схем:

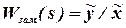 - передаточная функция замкнутой системы по управляющему воздействию (при );

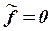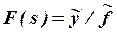 - передаточная функция замкнутой системы по возмущающему воздействию (при ).

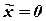Определенные таким образом передаточные функции САР записываются в виде соотношений:

; ;

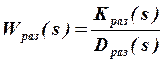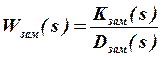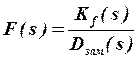
где K_раз(s); K_зам(s); K_f(s) - операторы возмущения; D_раз(s); D_зам(s)=D_раз(s)+K_зам(s) - собственные операторы разомкнутой и замкнутой САР, представляющие собой полиномы по переменной s. Например, для W_зам(s) оператор возмущения и собственный оператор можно представить так:

K_зам(s)=b₀s^m +b₁s^m-1 +...+b_m;

D_зам(s)=a₀sⁿ + a₁s^n-1 +... + a_n-1s + a_n,

где b_i; a_i - постоянные коэффициенты, зависящие от параметров и режима работы САР.

На основании полученных выражений для передаточных функций записываются операторные уравнения для системы в целом:

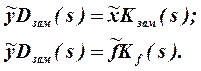
В этих уравнениях операторы возмущения K_зам(s); K_f(s) характеризуют возмущенное движение системы, а собственный оператор D_зам(s) - свободное движение системы регулирования. Передаточные функции САР и операторные уравнения системы в целом могут быть получены не только по структурной схеме, но и из решения системы операторных уравнений звеньев, что является иногда предпочтительным.

Область устойчивости замкнутой САР строится в плоскости выбранного (заданного) параметра, за который обычно выбирается коэффициент передачи или постоянная времени в которые входит легко изменяемый (перенастраиваемый) в процессе доводки САР физический параметр, например жесткость пружины, сопротивление дросселирующего элемента, давление питания рабочей жидкости гидроусилителей. Кривая D - разбиения (рис. 1.4) строится в следующем порядке:

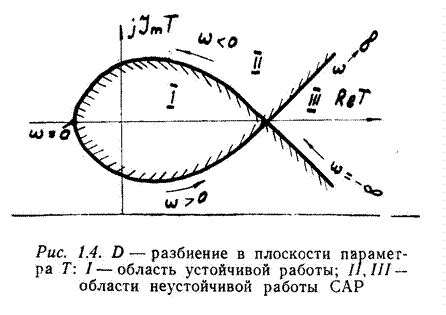а) записывается собственный оператор или характеристический полином замкнутой системы D_зам(s)= 0, который решается затем относительно исследуемого параметра, например, коэффициента Т;

 

б) подставив численные значения остальных коэффициентов, входящих в уравнение, и заменив s=jw, определяют комплексное выражение Т=ReT(w)+jImT(w);

в) на комплексной плоскости [ReT(w),jImT(w)] строится кривая D - разбиения, каждой точке которой соответствует вполне определенная частота колебаний w.

г) на кривой D - разбиения наносится штриховка с левой стороны по мере возрастания частоты w.

Переход через кривую D - разбиения с не заштрихованной стороны в заштрихованную соответствует смене знака вещественной части одного корня характеристического уравнения с “+“ на “-“, т.е. переходу системы в более устойчивое состояние и наоборот. С использованием этого правила выделяется область изменения коэффициента Т, в которой реализуется большее число корней с отрицательной вещественной частью. Выбрав из этой области значение Т (по действительной оси), проверяют устойчивость САР. Если система устойчива, то она будет устойчива во всей выделенной области, если неустойчива, то никаким изменением параметра Т нельзя сделать систему устойчивой.

Устойчивость САР проверяется использованием алгебраического критерия устойчивости Рауса-Гурвица или частотных критериев Михайлова и Найквиста. При проверке устойчивости по критерию Рауса-Гурвица составляется определитель Гурвица:

где а₀; а₁;... а_п - коэффициенты собственного оператора системы D(s). Для устойчивости САР при а₀ > 0 необходимо и достаточно, чтобы определитель D и его п-1 диагональных минора (выделены штриховыми линиями) были положительны. Для системы с характеристическими уравнениями третьего порядка (п=3) определитель Гурвица записывается в виде

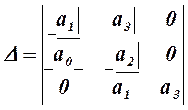
и при а₀ > 0 условие устойчивости выражается неравенствами: а₁ > 0; а₁а₂-а₀а₃ > 0; а₃ > 0.

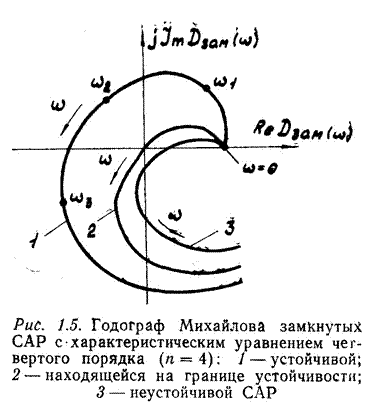
При проверке устойчивости САР по частотному критерию Михайлова на комплексной плоскости строится годограф Михайлова и анализируется его расположение относительно начала координат. Годограф Михайлова (рис. 1.5) строится по характеристическому полиному D_зам(s) заменой s=jw и представлением его в виде D_зам(jω)=ReD_зам(w)+jImD_зам(w). Каждой точке годографа Михайлова соответствует определенная частота колебаний w.

Для устойчивости САР необходимо и достаточно, чтобы при увеличении частоты колебаний w от 0 до ¥ вектор годографа Михайлова охватил последовательно в положительном направлении (против часовой стрелки) столько квадрантов (p/2), каков порядок характеристического полинома.

Критерии устойчивости Рауса-Гурвица и Михайлова применяются при анализе устойчивости как замкнутых, так и разомкнутых САР с соответствующими собственными операторами D_зам(s), D_раз(s).

 

Частотный критерий устойчивости Найквиста применяется при анализе устойчивости замкнутой САР по расположению ее амплитудно-фазочастотной характеристики (АФЧХ) в разомкнутом состоянии W_раз(jw) относительно точки на действительной оси с координатой (-1; j0). АФЧХ разомкнутой САР (рис. 1.6) строится по передаточной функции 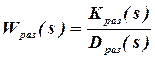 заменой s=jw и представлением ее в виде

W_раз(jw)= Re W_раз(w) + jIm W_раз(w).

При проверке устойчивости замкнутой САР по критерию Найквиста необходимо знать ее устойчивость в разомкнутом состоянии, причем, если разомкнутая САР неустойчива, то нужно знать, сколько корней характеристического полинома обладают положительной вещественной частью. Для этого анализируется собственный оператор разомкнутой САР D_раз(s) по критерию Рауса-Гурвица или Михайлова.

В технике, как правило, применяются устойчивые и нейтральные (содержащие в прямой цепи регулирования интегрирующее типовое звено) САР в разомкнутом состоянии. Поэтому в пособии приводится оценка устойчивости только таких систем.

 

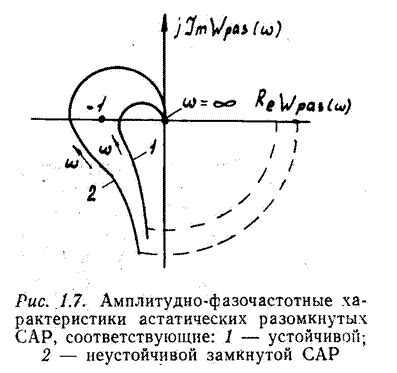
Для устойчивости замкнутой САР, устойчивой в разомкнутом состоянии, необходимо и достаточно, чтобы при изменении частоты колебаний w от -¥ до +¥ АФЧХ системы в разомкнутом состоянии не охватывала точку с координатой  ( -1; j0 ) (см. рис. 1.6). Это же правило справедливо и для нейтральных (астатических) разомкнутых САР (рис. 1.7). АФЧХ астатической САР берет начало (при w=0) в минус ¥ вдоль мнимой оси. При оценке устойчивости САР по критерию Найквиста такую АФЧХ дополняют другой бесконечно большого радиуса (см. рис. 1.7 - пунктирная линия). Более подробно с оценкой устойчивости по критерию Найквиста можно ознакомиться в специальной литературе [2, 3, 4].

Расчет границ D - разбиения в плоскости выбранного параметра, а также расчет частотных характеристик САР при оценке ее устойчивости облегчается, если воспользоваться персональным компьютером и специально разработанной программой расчета (см. разд. 2).

Строится переходная характеристика или переходная функция y(t ) и анализируется качество регулирования САР при ступенчатом управляющем x(t)=X₀[1(t)] или ступенчатом возмущающем f(t)=F₀[1(t)] воздействиях. Переходный процесс в САР определяется в результате интегрирования дифференциального уравнения САР при нулевых начальных условиях. Для САР, описываемой дифференциальным уравнением высокого порядка, переходный процесс определяется по вещественным частотным характеристикам систем или с использованием

цифровых вычислительных машин.

 

Для систем с дифференциальным уравнением до седьмого порядка можно воспользоваться разработанной программой расчета RADIS на персональном компьютере (см. разд. 2). В программе RADIS относительные величины ступеней управляющего и возмущающего воздействий заданы соответственно равными Х₀ = 1; F₀ = 1.

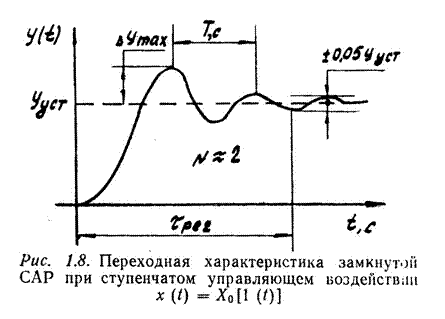
В результате построения и анализа переходной функции определяются основные показатели качества регулирования САР. При управляющем воздействии (рис. 1.8) такими показателями являются:

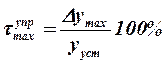- величина перерегулирования;

t_рег - время регулирования, в течение которого заканчивается переходный процесс в пределах заданной точности, например ± 5% от у_уст;

 - угловая частота собственных колебаний;

N - число периодов колебаний за время переходного процесса.

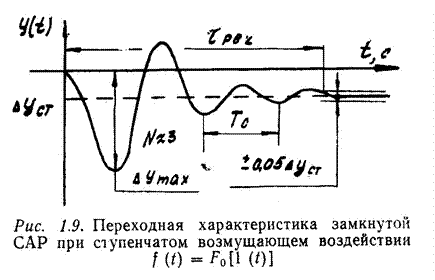При возмущающем воздействии (рис. 1.9) показателями качества регулирования являются:

 

 - величина перерегулирования;

Dу_ст - статическая ошибка регулирования;

t_рег - время регулирования, в течение которого заканчивается переходный процесс в пределах заданной точности, например ± 5% от у_ст для статической САР или ± 5% от Dу_тах для астатической САР;

N - число периодов колебаний за время переходного процесса;

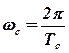 - угловая частота собственных колебаний САР.

Чем меньше значения показателей качества регулирования, тем лучше переходная характеристика САР, т.е. тем лучше работает регулятор. Оценка качества регулирования САР может проводиться и по другим показателям при других входных воздействиях, например при постоянной скорости нарастания управляющего или возмущающего воздействий.

Выбор параметров САР, при которых удовлетворяются заданные показатели качества регулирования, обычно осуществляется с использованием различных методов теории автоматического регулирования, например по распределению корней характеристического уравнения, по интегральным оценкам качества переходного процесса [2, 3, 4].

В курсовой работе при выборе параметров САР основное внимание уделяется ограничению перерегулирования и времени переходного процесса за счет изменения параметра D - разбиения. При этом из выделенной области устойчивости выбираются 2...4 положительных значения этого параметра и для каждого из них строится переходный процесс. Здесь следует иметь в виду, что при значениях параметров, взятых близко к границе устойчивости, реализуется колебательный переходный процесс с большим перерегулированием. При расчетах может оказаться так, что изменением только данного параметра не удается получить желаемый переходный процесс. В этих случаях в курсовой работе следует ограничиться лучшим вариантом переходного процесса, достигнутым за счет изменения параметра D - разбиения.

Пояснительная записка и графики динамических характеристик САР оформляются в соответствии с общими требованиями к оформлению технической документации [5].

 

2. АЛГОРИТМ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК САР

Исследование динамических характеристик САР на ЭВМ с самостоятельной разработкой алгоритмов и программ расчета приходит к большим затратам времени исследователя и не позволяет ему сосредоточить основное внимание на анализе решения самой задачи. Поэтому разрабатываются программы решения стандартных задач динамики систем, реализация которых в диалоговом режиме дает высокий эффект в обучении и приобретении навыков исследования САР с использованием ЭВМ.

В данном разделе пособия приведены алгоритм расчета частотных и переходных характеристик САР.

Исходными данными при расчете динамических характеристик САР являются: выражение для параметра D-разбиения, представленного в операторной форме; передаточные функции САР.

При расчете D-разбиения в плоскости параметра T(s) исходная зависимость представляется в следующей стандартной форме:

           (2.1)

где b₀,...,b_m; a₀,...,a_n - постоянные коэффициенты, зависящие от параметров САР. В программе расчета D -разбиения предусмотрены замена s=jw, выделение действительной и мнимой частей числителя и знаменателя частотной функции T(jw):

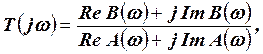
где

 

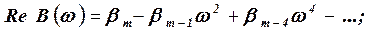
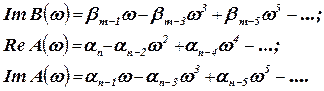
Результаты расчета представляются в следующей форме:

где 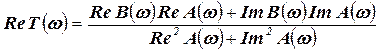 -действительная часть частотной функции;

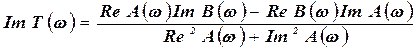 -мнимая часть частотной функции;

 -модуль частотной функции;

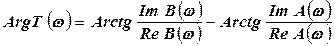 -аргумент частотной функции T(w).

Устойчивость САР по частотному критерию Михайлова определяется по собственному оператору замкнутой (разомкнутой) САР, заданной в виде

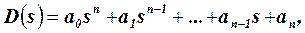
где a₀,... a_n - коэффициенты, зависящие от параметров САР. В программе расчета предусмотрена замена s=jw и определение частотной функции D(jw):

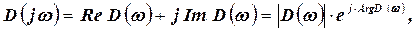
где 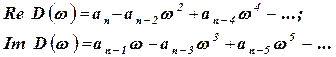  - действительная и мнимая часть частотной функции;

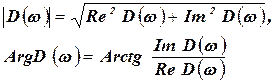- модуль частотной функции и ее аргумент.

При оценке устойчивости замкнутой САР по критерию Найквиста передаточная функция системы в разомкнутом состоянии записывается в виде

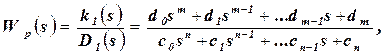
где c₀,..., c_n, d₀,..., d_m - постоянные коэффициенты, зависящие от параметров системы. Алгоритм расчета АФЧХ разомкнутой САР аналогичны алгоритму расчета D -разбиения [см. формулу (2.1)].

Определение переходной характеристики производится по передаточной функции САР по управляющему или возмущающему воздействию:

                    (2.2)

Выражение (2.2) соответствует линейному дифференциальному уравнению

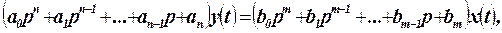(2.3)

где y(t) - регулируемый параметр; x(t) - управляющее или возмущающее воздействия; a₀,...,a_n, b₀,..., b_m - постоянные коэффициенты; 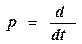 - оператор дифференцирования. Для отыскания решения уравнения (2.3) необходимо определить корни характеристического уравнения и постоянные интегрирования, учитывающие начальные условия. Операция вычисления корней и решение системы уравнения для отыскания постоянных интегрирования представляет собой трудоёмкий процесс, особенно для систем высокого порядка. Расчеты получаются более простыми в том случае, когда правая часть (2.3) равна нулю, т.е. имеется однородное дифференциальное уравнение.

Для типового входного воздействия вида единичной ступенчатой функции сведение неоднородного уравнения (2.3) к однородному может быть выполнено переходом к другой переменной [2]. Предполагается, что x(t)=1(t), причем единица имеет размерность переменной, стоящей в правой части (2.3). Тогда установившееся значение y(t) при t®  можно найти из (2.3), предполагая все производные равные нулю:

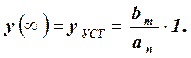
Это установившееся значение представляет собой частное решение неоднородного уравнения (2.3), т.е.

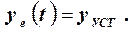
Вводится новая переменная

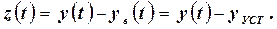
Тогда уравнение (2.3) с новой переменной перепишется в виде

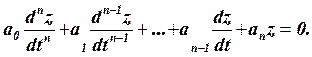                 (2.4)

Решение однородных уравнений не представляет затруднений.

При известном решении z(t ) переход к переменной y(t) осуществляется по формуле

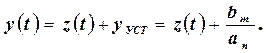
При решении уравнений используются начальные условия до ступенчатого воздействия (y_-0) и после (y₊₀) и эти условия будут различные. Для простоты расчетов для времени t=-0 (до воздействия) почти всегда принимают нулевые начальные условия, т.е. 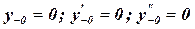 и т.д. В дальнейшем под нулевыми начальными условиями будут иметься в виду именно эти равенства.

Начальные условия, реализующиеся непосредственно после приложения ступенчатого воздействия, т.е. при t=+0, можно определить из исходного дифференциального уравнения (2.3).

Для первых n-m начальных условий имеют место равенства:

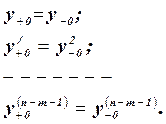
Таким образом для самой переменной y и первых (n-m-1) производных начальные условия сохраняются и после приложения ступенчатого воздействия. Для остальных начальных условий выполняются соотношения:

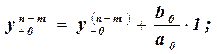
В формулах (2.5) множитель 1 имеет размерность x(t). Если воздействие прикладывается в виде скачка, не равного единице, то вместо 1 следует поставить величину скачка. Из формул (2.5) ясно, что только при m=0, т.е. для дифференциального уравнения D(p)y(t)=b_mx(t) при ступенчатом воздействии начальные условия при t=+0 соответствуют начальные условия при t=-0.

Интегрирование дифференциального уравнения (2.4) производится численным методом Ренге-Кутта четвертого порядка [6].

Рис 2.1?

3. ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК САР ЧАСТОТЫ ВРАЩЕНИЯ ГТД