Начальные и граничные условия

Раздел №3. Математическая постановка краевых задач

Уравнение теплопроводности (диффузии) является дифференциальным уравнением в частных производных относительно функции двух переменных T(x,t). Пространственную переменную x будем считать изменяющейся на ограниченном отрезке [0,l], а время – . Уравнение теплопроводности имеет первый порядок по времени и второй порядок по пространственной координате x. (Такие уравнения называются уравнениями параболического типа). Так же как и обыкновенное дифференциальное уравнение, где искомая функция зависит от одной переменной, уравнение в частных производных имеет бесконечное множество частных решений. В теории обыкновенных дифференциальных уравнений для выделения нужного частного решения задаются дополнительные условия – начальные или граничные. Точно так же для нахождения нужного частного решения уравнения в частных производных должны быть заданы аналогичные условия. При этом, поскольку искомая функция зависит от двух переменных, эти дополнительные условия должны быть заданы по каждой переменной. Дополнительные условия по времени называются начальными условиями, а дополнительные условия по пространственной координате называются граничными условиями, вместе их называют краевыми условиями. Поскольку уравнение (2.5) имеет первый порядок по времени, то начальное условие только одно, и записывается оно в виде значения искомой функции в начальный момент времени

          .                                                  (2.6)

Относительно дополнительных условий по пространственной координате x имеется гораздо большее разнообразие. А именно, существует три типа граничных условий: граничные условия 1-го, 2-го, 3-го рода. Сформулируем все три типа для одномерного уравнения теплопроводности и диффузии.

Граничные условия 1-го рода. В этом случае, на границе области, где изучается процесс, задается значение искомой функции (температуры или концентрации)

В одномерном случае граница состоит из двух частей, задаваемых уравнениями x=0 и x=l, поэтому граничные условия запишутся так

           или ,

где f1(t), f2(t) — заданные функции времени, а .

Граничные условия 2-го рода. Здесь на границе области задается не сама искомая функция, а ее тепловой или диффузионный поток. (т.е. в случае граничных условий 2-го рода задается производная искомой функции по направлению внешней нормали к поверхности). В соответствии с законами Фурье и Нернста граничное условие 2-го рода для одномерного случая имеет вид (отдельно для теплопроводности и диффузии)

          и       (2.7)

Граничные условия первого и второго рода называются однородными, если они равны нулю.

Физически однородные граничные условия второго рода означают тепловую изоляцию поверхности или ее непроницаемость для диффундирующего вещества.

Граничные условия 3-го рода. Это условие тепло- или массообмена с окружающей средой. Для теплопроводности процесс теплообмена описывается законом Ньютона – Рихмана, согласно которому количество теплоты, которое отдает или получает малый участок поверхности DS за малое время Dt, пропорционально разности температур поверхности и окружающей среды, т.е.

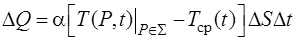           ,                                        (2.9)

где α – относительный коэффициент теплообмена [α] = [кал/(см2 сек град)],  – точка на границе области.

С другой стороны, количество теплоты, которое переносится через тот же участок DS за то же время Dt определяется законом Фурье

          .

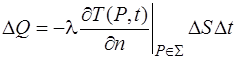Приравнивая, получаем

          или

           ,

где  – коэффициент теплообмена [ h ] = [1/см].

В одномерном случае это будет

.

Однородные граничные условия третьего рода, когда температура окружающей среды равна нулю, имеют вид

          .

Для диффузии граничные условия третьего рода записываются аналогично

.

Соответственно однородные граничные условия третьего рода, когда концентрация вещества в окружающей среде равна нулю, имеют вид

          .

Ранее выведенные основные уравнения теплопроводности (диффузии) содержат пространственную переменную x и время t. Для этих уравнений рассмотрим модельные задачи на примере тонкого стержня или бесконечной пластины, когда 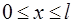. В краевую задачу входят следующие составляющие:

· уравнение теплопроводности вместе с областью определения уравнения по пространственным переменным и времени, причем только во внутренних точках областей для x и t;

· начальное условие для области по x берется из эксперимента;

· граничные условия при x = 0, x = l берутся из эксперимента.