Сложение пар. Условия равновесия пар

Теорема о сложении пар, лежащих в одной плоскости. Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.

Доказательство: пусть на тело действуют три пары с моментами 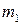, , 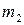 (рис. 4.7, а). На основании теоремы об эквивалентности пар их можно заменить тремя парами 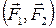, , 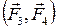, 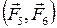имеющими общее плечо  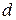и такие же моменты: 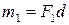, ,  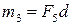(рис. 4.7, б). Складывая отдельно силы, приложенные в точках  и , получаем в точке  силу , а в точке  – силу ,  которые  по  модулю  будут  равны:  (рис. 4.7, в).

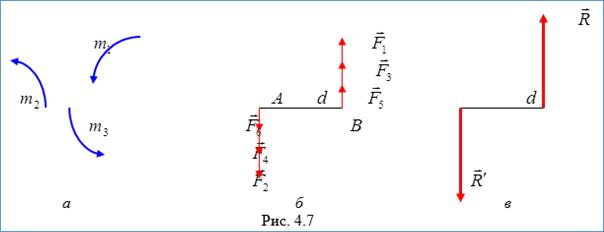
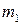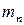В результате вся система пар заменяется одной парой  с моментом . Для случая из  пар с моментами , , …  система заменяется одной парой с моментом . Если пары расположены в пространстве, то можно перейти к векторному равенству . Проектируя это векторное равенство на оси декартовой системы координат, получаем

, , .

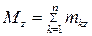Отсюда следует условие равновесия системы пар: для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары был равен нулю .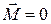

Геометрическое условие равновесия:для равновесия произвольной системы пар необходимо и достаточно, чтобы векторный момент результирующей пары был равен нулю .

Аналитическое условие равновесия: 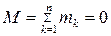 или через проекции на оси , , .

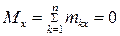Практическое занятие

Система пар сил

    Дано. Куб со стороной , изображенный на рисунке 4.8, а подвешен к двум вертикальным стержням  и  так, что его диагональ  горизонтальна. К кубу приложены пары сил , . Пренебрегая весом куба, определить при каком соотношении между силами этих пар, он будет в равновесии и чему при этом равны реакции стержней.

    Решение. Система пар  и  эквивалентна одной паре, может быть уравновешена только парой сил. Следовательно, искомые реакции  и  должны образовывать пару.

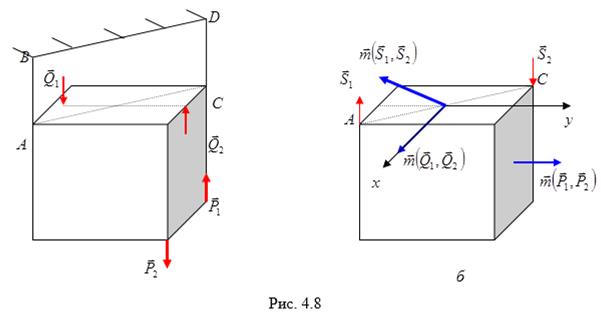
Ее момент, направленный перпендикулярно диагонали , проведен так, как показано на рис. 4.8, б. При этом по модулю . Моменты заданных пар обозначим , . Направления векторов 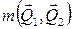 и   показаны на рис.4.8, б. Проводя оси координат, составляем условия равновесия:

, ,

, , .

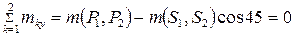    Таким образом, равновесие возможно, когда . Реакции стержней также равны по модулю  и направлены вдоль самих стержней (рис. 4.8, б).

    Ответ: .