Нахождение обратной матрицы методом Гаусса-Жордана

Существуют альтернативные методы нахождения обратной матрицы, например, метод Гаусса - Жордана.

Суть метода Гаусса-Жордана заключается в том, что если с единичной матрицей Е провести элементарные преобразованиия, которыми невырожденная квадратная матрица А приводится к Е, то получится обратная матрица .

Опишем алгоритм приведения матрицы А порядка n на n, определитель которой не равен нулю, к единичной матрице методом Гаусса - Жордана. После описания алгоритма разберем пример, чтобы все стало понятно.

Сначала преобразуем матрицу так, чтобы элемент стал равен единице, а все остальные элементы первого столбца стали нулевыми.

Если , то на место первой строки ставится k-ая строка (k>1), в которой 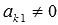, а на место k-ой строки ставится первая. (Строка с 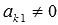обязательно существует, в противном случае матрица А – вырожденная). После перестановки строк получили «новую» матрицу А, у которой .

Теперь умножаем каждый элемент первой строки на . Так приходим к «новой» матрице А, у которой . Далее к элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на . К элементам третьей строки – соответствующие элементы первой строки, умноженные на . И продолжаем такой процесс до n-ой строки включительно. Так все элементы первого столбца матрицы А, начиная со второго, станут нулевыми.

С первым столбцом разобрались, переходим ко второму.

Преобразуем матрицу А так, чтобы элемент стал равен единице, а все остальные элементы второго столбца, начиная с , стали нулевыми.

Если , то на место второй строки ставится k-ая строка (k>2), в которой , а на место k-ой строки ставится вторая. Так получаем преобразованную матрицу А, у которой . Умножаем все элементы второй строки на . После этого к элементам третьей строки прибавляем соответствующие элементы второй строки, умноженные на . К элементам четвертой строки – соответствующие элементы второй строки, умноженные на . И продолжаем такой процесс до n-ой строки включительно. Так все элементы второго столбца матрицы А, начиная с третьего, станут нулевыми, а будет равен единице.

Со вторым столбцом закончили, переходим к третьему и проводим аналогичные преобразования.

Так продолжаем процесс, пока все элементы главной диагонали матрицы А не станут равными единице, а все элементы ниже главной диагонали не станут равными нулю.

С этого момента начинаем обратный ход метода Гаусса-Жордана. Теперь преобразуем матрицу А так, чтобы все элементы n-ого столбца, кроме 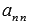, стали нулевыми. Для этого к элементам (n-1)-ой строки прибавляем соответствующие элементы n-ой строки, умноженные на . К элементам (n-2)-ой строки – соответствующие элементы n-ой строки, умноженные на . И продолжаем такой процесс до первой строки включительно. Так все элементы n-ого столбца матрицы А (кроме 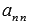), станут нулевыми.

С последним столбцом разобрались, переходим к (n-1)-ому.

Преобразуем матрицу А так, чтобы все элементы (n-1)-ого столбца до , стали нулевыми. Для этого к элементам (n-2)-ой строки прибавляем соответствующие элементы (n-1)-ой строки, умноженные на . К элементам (n-3)-ой строки – соответствующие элементы (n-1)-ой строки, умноженные на . И продолжаем такой процесс до первой строки включительно. Так все элементы (n-1)-ого столбца матрицы А (кроме ), станут нулевыми.

Действуя дальше схожим образом, мы получим единичную матрицу.

Пример.

Приведите матрицу к единичной с помощью преобразований Гаусса – Жордана.

Решение.

Так как , а , то переставим местами первую и вторую строки матрицы, получим матрицу .

Умножим все элементы первой строки матрицы на : .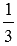

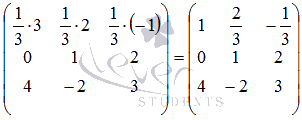К элементам второй строки прибавляем соответствующие элементы первой строки, умноженные на 0, а к элементам третьей строки прибавляем соответствующие элементы первой строки, умноженные на (-4):

Переходим ко второму столбцу.

Элемент полученной матрицы уже равен единице, поэтому нет необходимости производить умножение элементов второй строки на . К элементам третьей строки прибавляем соответствующие элементы второй строки, умноженные на :

Переходим к третьему столбцу.

Умножим элементы третьей строки на : .

Единицы на главной диагонали матрицы получены, так что приступаем к обратному ходу.

К элементам второй строки прибавляем соответствующие элементы третьей строки, умноженные на (-2), а к элементам первой строки прибавляем соответствующие элементы третьей строки, умноженные на :

В последнем столбце необходимые нулевые элементы получены, переходим к предпоследнему (ко второму) столбцу.

К элементам первой строки прибавим соответствующие элементы второй строки, умноженные на : .

Так проведены все преобразования матрицы и получена единичная матрица.

Пришло время применить метод Гаусса – Жордана к нахождению обратной матрицы.

Пример.

Найдите обратную матрицу для методом Гаусса – Жордана.

Решение.

В левой части страницы будем проводить преобразования Гаусса – Жордана с матрицей А, а в правой части страницы будем проделывать те же преобразования с единичной матрицей.

Так как , а , то переставим первую и вторую строки местами:

Умножим элементы первой строки матрицы на одну вторую, чтобы элемент стал равен единице:

К элементам второй строки прибавим соответствующие элементы первой строки, умноженные на 0, к элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на 2, к элементам четвертой строки – элементы первой строки, умноженные на 5:

Так в первом столбце матрицы А мы получили нужные нулевые элементы. Переходим ко второму столбцу. Добьемся того, чтобы элемент стал равен единице. Для этого умножим элементы второй строки матрицы на 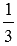, не забываем выполнять такие же преобразования с матрицей в правой части:

Дальше нам нужно сделать элементы и нулевыми, для этого к элементам третьей строки прибавляем соответствующие элементы второй строки, умноженные на 0, а к элементам четвертой строки прибавляем соответствующие элементы второй строки, умноженные на :

Так второй столбец матрицы А преобразован к нужному виду. Переходим к третьему столбцу. Так как элемент нулевой, то меняем местами третью и четвертую строки:

Умножаем элементы третьей строки на :

Третий столбец матрицы А принял нужный вид (элемент нулевой, поэтому не пришлось к элементам четвертой строки прибавлять соответствующие элементы третьей строки, умноженные на ). Осталось умножить четвертую строку на чтобы все элементы главной диагонали стали равны единице:

Прямой ход метода Гаусса-Жордана завершен, приступаем к обратному ходу. Получаем необходимые нулевые элементы в последнем столбце матрицы А. Для этого к элементам третьей строки прибавляем соответствующие элементы последней строки, умноженные на , к элементам второй строки – элементы последней строки, умноженные на , к элементам первой строки – элементы последней строки, умноженные на 0:

Получаем нули в предпоследнем столбце прибавлением к элементам второй и первой строк соответствующие элементы третьей строки, умноженные на 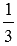и 0 соответственно:

Осталось последнее преобразование. К элементам первой строки прибавляем элементы второй строки, умноженные на :

Итак, матрица А преобразованиями Гаусса – Жордана приведена к единичной матрице, а единичная матрица с помощью таких же преобразований приведена к обратной матрице. Таким образом, в правой части получена обратная матрица. Можете провести проверку, выполнив умножение матрицы А на обратную матрицу.

Ответ:

.