| 1. | 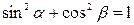
| 4. | 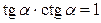
|
| 2. | 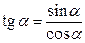
| 5. | 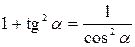
|
| 3. | 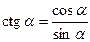
| 6. | 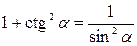
|
Формулы сложения
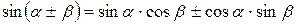
|
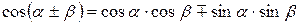
|
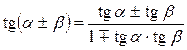
|
Формулы двойных и половинных углов
| 1. | 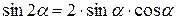
| 5. | 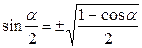
|
| 2. | 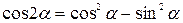
| 6. | 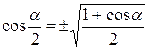
|
| 3. | 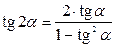
| 7. | 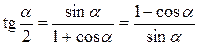
|
| 4. | 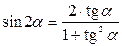
| 8. | 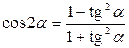
|
Формулы преобразования суммы в произведение
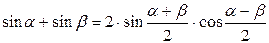
| 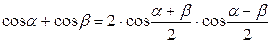
|
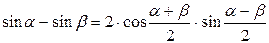
| 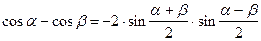
|
Формулы преобразования произведения в сумму
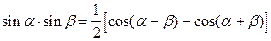
|
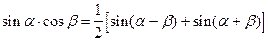
|
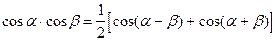
|
Примеры решения задач
Пример 1
Доказать тождество:
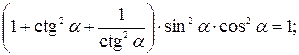
Решение. Приведем левую часть к 1:
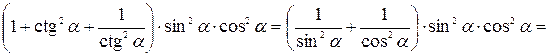
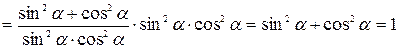 .
.
Пример 2
Вычислить значение выражения:
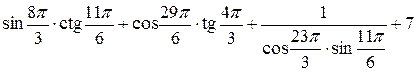
Решение. Используя формулы приведения, получим:
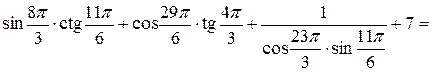
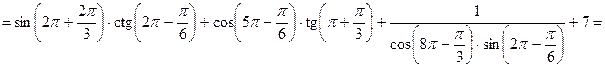
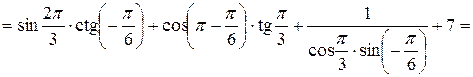
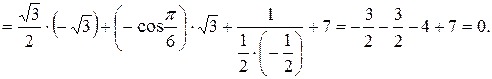
Пример 3 Упростите выражения:
1. 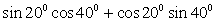
2. 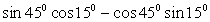
3. 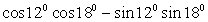
4. 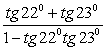
5. 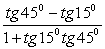 .
.
Решение
Данные задания — на применение формул сложения.
1. 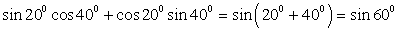
2. 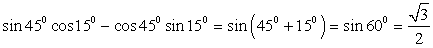
3. 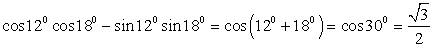
4. 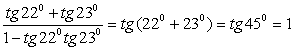
5. 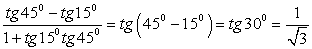 .
.
Ответ: 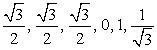
Пример 4 Вычислите:
1) 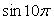 ;2)
;2) 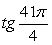 ;3)
;3) 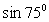 ;4)
;4) 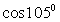 ;5)
;5) 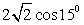 .
.
Решение
1) Воспользуемся свойством периодичности функции y = sin x, тогда 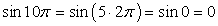
2) Так как период функции y = tg x равен π, получаем: 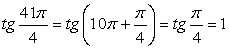
3) Представим 75º в виде суммы двух «удобных» слагаемых: 75º = 45º + 30º. Следовательно, 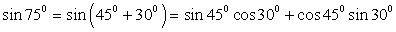 . Обратимся к табличным значениям тригонометрических функций, получим:
. Обратимся к табличным значениям тригонометрических функций, получим: 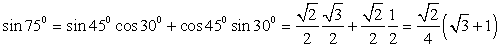 4)
4) 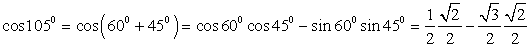 . Окончательно получаем, что
. Окончательно получаем, что 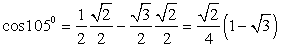
5) Для вычисления значения cos 15º представим 15º как 15º = 45º - 30º (или 15º = 60º - 45º). Тогда 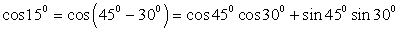 . Получаем, что
. Получаем, что 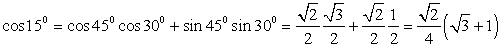 . Cледовательно,
. Cледовательно, 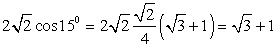 .
.
Ответ: 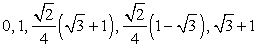 .
.
Пример 6
Вычислить sin10º sin30º sin50º sin70º.
Решение:
Используем формулу преобразования произведения тригонометрических функций в сумму: sin10º sin50º = 1/2 (cos40º - cos60º) = 1/2 cos 40º- 1/4. Подставим в первоначальное произведение это выражение и учтем, что sin30º = 1/2, получаем: 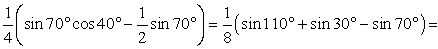
Ответ: 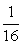
Практические задания
Вариант
1. 1+ 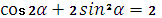
2. 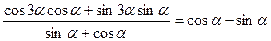
3. 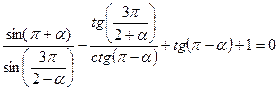

4. 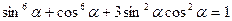

5. 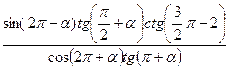
2 Вариант
1. 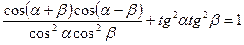
2. 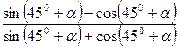
3. 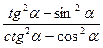
4. 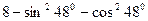
5. 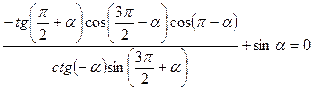
Вариант
1) 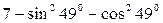
2) 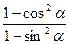
3) 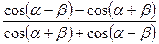
4) 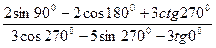
5) 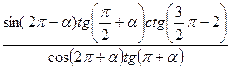
Вариант
1) 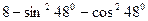
2) 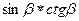
3) 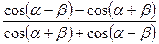
4) 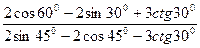
5) 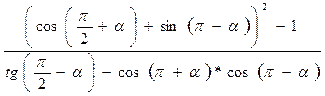
УЧЕБНАЯ КАРТА ПРАКТИЧЕСКОГО ЗАНЯТИЯ №4
.
| Дата | Группа |
| 1111 | |
| 1211 | |
| 1311 | |
| 1411 | |
| 1511 |
 2020-05-11
2020-05-11 274
274








