Методические рекомендации

Тема 1. Свойства дробей

1.1. Как изменится правильная дробь, если ее числитель и знаменатель увеличить на одно и тоже натуральное число, меньшее знаменателя? Высказанное предположение докажите.

1.2. Докажите, что если дробь  сократима, то дроби  тоже сократимы.

1.3. Верно ли, что при любом натуральном n числитель и знаменатель дроби  делятся на 6? Ответ обоснуйте.

1.4. Известно, что дроби   равны и числитель первой дроби меньше числителя второй. Докажите, что в этом случае n <q.

Методические рекомендации

В данной теме представлены два типа задач. К первому относятся те, в которых исследуется вопрос о том, как изменяется данная дробь, если к ее числителю и знаменателю прибавить (вычесть) одно и то же число. Их решение основано на следующем свойстве отношения «больше» для чисел a и b: a>b тогда и только тогда, когда a-b>0.

Задачи второго типа связаны с понятием сократимой и несократимой дроби.

Для решения задач данной темы необходимо

Образец выполнения задания

Задача 1. Докажите, что правильная дробь уменьшится, если из ее числителя и знаменателя вычесть одно и то же натуральное число, меньшее числителя.

Решение: Запишем задачу, используя символы. Пусть  - правильная дробь, а  -такое натуральное число, что с< a. Если из числителя и знаменателя данной дроби вычесть с, то получим дробь . Покажем, что  > .

Рассмотрим разность  - . Если она окажется положительной, то данное утверждение будет доказано.

Используя правило вычитания дробей и свойства действий над натуральными числами, преобразуем эту разность:

 -  =  =  =  = .

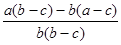В последней дроби разность   положительна, т.к. по условию дробь - правильная, значит, b>a. Разность b-c тоже положительна, т.к. b>c (по условию c<a, a<b, но тогда по свойству транзитивности отношения «меньше» c<b или b>c). Значит, >0, поэтому > , что и требовалось доказать.

Задача 2. Докажите, что числитель и знаменатель дроби 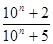   делятся на 3.

Решение: Воспользуемся признаком делимости на 3. Сумма цифр в записи числителя равна 3 (сумма цифр числа 10ⁿ равна 1, т.к. 10ⁿ =100...0). Соответственно сумма цифр знаменателя равна 6, но 6 кратно 3. Следовательно, числитель и знаменатель дроби делятся на 3.