Дифференциальный принцип механики систем с геометрическими (голономными) связями

При движении системы 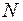 твёрдых тел в любом ее положении, допускаемом геометрическими связями, сумма элементарных работ всех сил взаимодействий и всех сил инерций равна нулю на любых элементарных перемещениях системы (совместимых или не совместимых со связями):

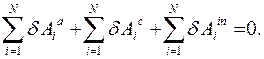
Принцип (аксиома) применим для любого количества 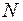 твердых тел механической системы.

   Дифференциальный принцип механики на виртуальных перемещениях: принцип Даламбера – Лагранжа.

Дифференциальный принцип механики на Возможных (виртуальных) перемещениях применяют для нахождения движения системы. Принцип дает возможность написать дифференциальные уравнения движения системы в случаях, когда элементарная работа всех сил контактного взаимодействия системы равна нулю:

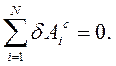
В таком случае говорят, то есть при идеальных связях.

В этом случае из дифференциального принципа следует, что

сумма элементарных работ всех активных сил и всех сил инерций системы равна нулю на любых виртуальных перемещениях системы:

Эту форму дифференциального принципа называют принцип Даламбера - Лагранжа.

Используя уравнения связей, вектор положения точек тела 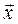 и его вариацию  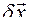можно выразить через обобщенные координаты  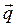 и их виртуальные перемещения . 

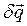Поэтому принцип Даламбера - Лагранжа можно представить в следующем виде:

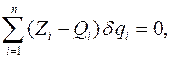
где                       .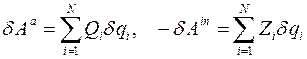

В силу независимости и произвольности виртуальных перемещений 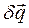, уравнение дифференциального принципа     распадаются на n уравнений

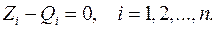
Эти уравнения есть дифференциальные уравнения движения системы тел с идеальными связями в обобщенных координатах.

Они не включают неизвестные силы контактных взаимодействий.

Для системы 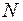  поступательно движущихся тел (материальных точек)  принцип запишется в виде:

 

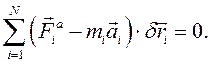
 Консервативнаясистема. Положения равновесия консервативных систем.

Консервативная система имеет геометрические стационарные связи, сумма            элементарных работ сил реакций идеальных связей равна нулю, а все работающие силы потенциальны.

Положения равновесия определяются свойствами сил взаимодействий и            виртуальными перемещениями в этих положениях.

А именно: в каждом положении равновесия равны нулю виртуальные работы силового поля и сил реакций связей на любых виртуальных перемещениях:

  .

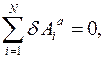
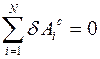Это свойство сил взаимодействий примем за определение положений   равновесия.

Так как для потенциальных сил в положениях равновесия виртуальную работу активных сил можно выразить через дифференциал потенциальной энергии, то есть

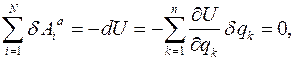
то равенство нулю полного дифференциала 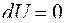 потенциальной энергии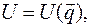 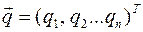, означает, что положения равновесия доставляют экстремум потенциальной энергии.

Следующее определение положений равновесия консервативной системы тождественно предыдущему.

 Положениями равновесия консервативной системы с идеальными связями называются такие положения системы 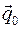, совместимые со связями, в которых потенциальная энергия системы   U  принимает экстремальные значения:

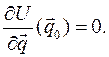
Это определение не связано с движениями системы, и, таким образом, не зависит от начальных состояний системы (начальных положений и начальных скоростей тел).

Так как связи системы идеальны, то из принципа Даламбера – Лагранжа следует, что на движениях системы в положениях равновесия равна нулю и виртуальная работа сил инерций.

Пример 1. Математический маятник: материальная точка   М   движется по части окружности   в вертикальной плоскости. В нижней точке, 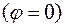, равны нулю виртуальные работы силы тяжести и силы реакции нити. Это есть положение равновесия. маятника. Так как скорость точки в положении равновесия имеет максимум, то касательное ускорение в нем равно нулю. Поэтому сила инерции точки, определяемая нормальным ускорением, перпендикулярна виртуальному перемещению и не работает на нем.

Заметим, что на границе интервала виртуальная работа силы тяжести (и силы инерции) не равны нулю, поэтому граница интервала не есть положение равновесия, хотя потенциальная энергия маятника в ней имеет максимум.

Пример 2. Сферический маятник: материальная точка подвешена на нити в точке О, центре сферы. Хотя сила тяжести и сила реакции нити не работают на элементарных перемещениях, векторы которых являются касательными векторами к параллелям сферы, однако они работают на виртуальных перемещениях, касательных к меридианам сферы. В нижней точке сферы эти силы не работают на всех виртуальных перемещениях, поэтому нижняя точка сферы есть  положение равновесия маятника.

Пример 3. Система состоит из однородного тонкого стержня АВ с массой М и груза D  с массой 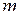 , соединенного со стержнем невесомой нитью. При гладкости плоскостей консервативная система с одной степенью свободы имеет идеальные связи. При произвольных массах тел в системе нет положений равновесия. Но если , то все положения системы, допустимые связями 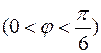, есть безразличные положения равновесия. Это видно из принципа виртуальных перемещений, который можно записать в следующем виде:

 

 

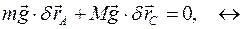
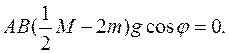
  Дифференциальный принцип механики для систем в положениях равновесия, состоянии равновесия и в покое.

Если механическая система с идеальными связями находится в покое на конечном интервале времени, то равны нулю все силы инерции. Тогда

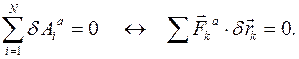
Используя обобщенные координаты системы и их вариации 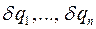,   принцип виртуальных перемещений можно записать в следующем виде:

      

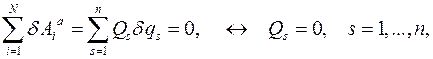
где 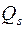 есть обобщенные силы системы.