Плотностью распределения вероятностей f(x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.:
f(x)=F’(x)
Математическое ожидание М (Х) непрерывной случайной величины Х определяются равенством:
+∞
M(X)= ∫ x•f(x)dx,
-∞
при условии, что этот интеграл сходится абсолютно.
Дисперсия D(X) непрерывной случайной величины Х определяется равенством:
+∞
D(X)= ∫ (х-М(х)2)•f(x)dx, или
-∞
+∞
D(X)= ∫ х2•f(x)dx- (М(х))2
-∞
Среднее квадратическое отклонение σ(Х) непрерывной случайной величины определяется равенством:
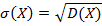
Пример решения задач
Случайная величина Х задана плотностью распределения вероятностей:
0 при х≤2,
f(x)= с(х-2) при 2<х≤6,
0 при х>6.
Найти: а) значение с; б) функцию распределенияF(х) и построить ее график; в)Р(3≤х<5)
+∞ 2 6 +∞ 6 6
∫ f(x)dx=∫ 0dx+ ∫ c(х-2)dx +∫ 0dx= c∫ (х-2)dx=с(х2/2-2х) =с(36/2-12-(4/2-4))=8с;
-∞ -∞ 2 6 2 2
8с=1;
с=1/8. х
б) Известно, что F(x)= ∫ f(x)dx
-∞
Поэтому, х
если х≤2, то F(x)= ∫ 0dx=0;
-∞ 2 2 х
если 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х2/2-2х) = 1/8(х2/2-2х- (4/2-4))=
-∞ -∞ 2
=1/8(х2/2-2х+2)=1/16(х-2)2;
2 6 х 6 6
если х>6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx+∫ 0dx=1/8∫(х-2)dx=1/8(х2/2-2х) =
-∞ 6 2 2 2
=1/8(36/2-12-(4/2+4))=1/8•8=1.
Таким образом,
0 при х≤2,
F(х)= (х-2)2/16 при 2<х≤6,
1 при х>6.
График функции F(х) изображен на рис.
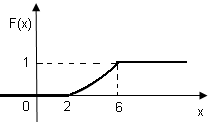
в) Р(3≤Х<5)=F(5)-F(3)=(5-2)2/16-(3-2)2/16=9/16-1/16=5/16.
Задачи
1. Случайная величина Х задана функцией распределения
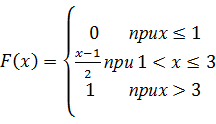
Чему равна вероятность того, что в результате испытания Х примет значение из интервала (0,2; 0,7)
2. Случайная величина Х задана функцией распределения
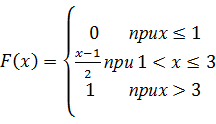
Чему равна вероятность того, что в результате испытания Х примет значение из интервала (3,3; 4,6)
3. Случайная величина Х задана функцией распределения
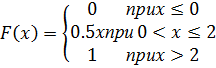
Чему равна вероятность того, что в результате испытания Х примет значение из интервала (2,3; 4,6)
4. Случайная величина Х задана функцией распределения
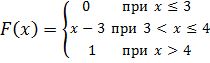
Чему равна вероятность того, что в результате испытания Х примет значение из интервала (2,3; 2,9)
5. Случайная величина X задана функцией распределения
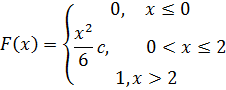
Найдите коэффициент с.
6. Случайная величина X задана функцией распределения

Найдите коэффициент с.
7. Случайная величина Х задана функцией распределения 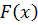 :
:
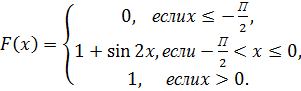
Найдите плотность вероятности 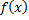 .
.
8. Случайная величина Х задана функцией распределения 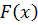 :
:

Найдите плотность вероятности 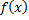 .
.
9. Случайная величина Х задана функцией распределения 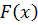 :
:
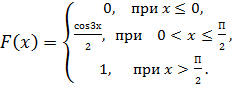
Найдите плотность вероятности 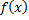 .
.
10. Случайная величина Х задана функцией распределения 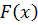 :
:
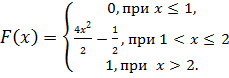 ,
,
Найдите плотность вероятности 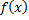 .
.
11. Случайная величина 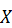 на отрезке [1,2] задана плотностью распределения
на отрезке [1,2] задана плотностью распределения 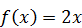 , вне этого отрезка
, вне этого отрезка 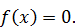 Найдите математическое ожидание данной случайной величины.
Найдите математическое ожидание данной случайной величины.
12. Случайная величина 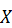 на отрезке [0,2] задана плотностью распределения
на отрезке [0,2] задана плотностью распределения 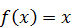 , вне этого отрезка
, вне этого отрезка 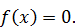 Найдите математическое ожидание данной случайной величины.
Найдите математическое ожидание данной случайной величины.
13. Случайная величина 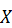 на отрезке [1,2] задана плотностью распределения
на отрезке [1,2] задана плотностью распределения 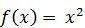 вне этого отрезка
вне этого отрезка 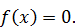 Найдите математическое ожидание данной случайной величины.
Найдите математическое ожидание данной случайной величины.
14. Случайная величина 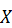 на отрезке [0, 2] задана плотностью распределения
на отрезке [0, 2] задана плотностью распределения 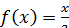 , вне этого отрезка
, вне этого отрезка 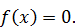 Математическое ожидание
Математическое ожидание 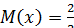 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.
15. Случайная величина 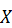 на отрезке [1, 2] задана плотностью распределения
на отрезке [1, 2] задана плотностью распределения 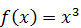 , вне этого отрезка
, вне этого отрезка 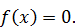 Математическое ожидание
Математическое ожидание 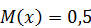 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.
16. Случайная величина 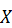 на отрезке [0, 1] задана плотностью распределения
на отрезке [0, 1] задана плотностью распределения 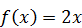 , вне этого отрезка
, вне этого отрезка 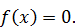 Математическое ожидание
Математическое ожидание 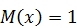 . Найдите дисперсию данной случайной величины.
. Найдите дисперсию данной случайной величины.
17. Случайная величина X задана функцией распределения
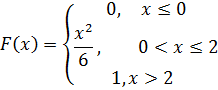
Найдите математическое ожидание данной случайной величины.
18. Случайная величина X задана плотностью распределения
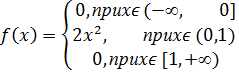
Найдите функцию распределения 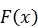 и её характеристики.
и её характеристики.
19. Случайная величина X задана плотностью распределения 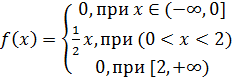
Найдите функцию распределения 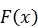 и её характеристики.
и её характеристики.
20. Функция распределения случайной величины Х имеет вид
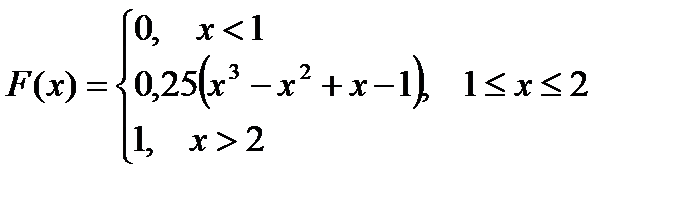
Найти 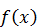 , M(X), D(X) и P (1 < х < 1,5).
, M(X), D(X) и P (1 < х < 1,5).
 2020-05-12
2020-05-12 248
248








