2020-05-12
574
Задача 1. Пассажирский поезд первую половину времени ехал со скоростью V1 = 60 км/ч, а вторую половину времени ехал со скоростью V2 = 90 км/ч. Товарный поезд первую половину пути ехал со скоростью V3 = 60 км/ч, а вторую половину пути – со скоростью V4 = 90 км/ч. На сколько средняя скорость VT товарного поезда больше средней скорости VП пассажирского поезда?
Решение
1) По определению средней скорости находим среднюю скорость пассажирского поезда:
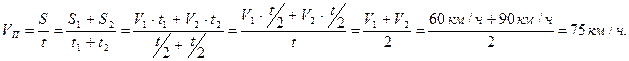
2) Также находим среднюю скорость товарного поезда:
. 
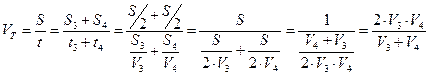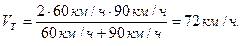
3) Средняя скорость пассажирского поезда на ΔV = 75 км/ч – 72 км/ч = = 3 км/ч больше средней скорости товарного поезда.
Задача 2. Тело, двигаясь равноускоренно и имея начальную скорость V0 = = 2 м/с, прошло за пятую секунду путь ΔS5 = 4,5 м. Определить путь, пройденный телом за время t = 10 с.
Решение
Путь, пройденный телом за время t, находится по формуле: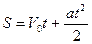 
.
Чтобы найти путь, пройденный телом за пятую секунду, надо из пути, пройденного телом за пять секунд, отнять путь, пройденный телом за четыре секунды:
|
|
|
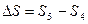, где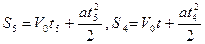 
.
Решая эти три уравнения, получаем: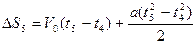 
. Для нахождения пути, пройденного телом за время t, вычисляем из полученного уравнения ускорение а:
.
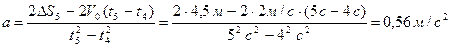Тогда путь, пройденный телом за время t, равен:
.
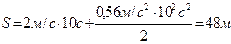Задача 3. С какой высоты Н тело свободно падает, если за последнюю секунду своего падения тело пролетело 3/4 всего пути? Сколько времени t тело падало?
Решение
Обозначим время, за которое тело пролетело 3/4 всего пути, через Δt = 1 с. По условию задачи V0 = 0. Тогда, применяя систему кинематических уравнений, описывающих свободное падение, получим уравнение для нахождения высоты Н:
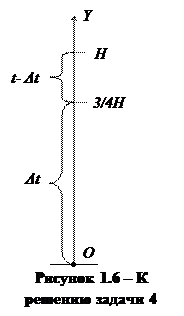
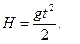(1)
В этом уравнении две неизвестных величины H и t. Составляем второе это уравнение с этими неизвестными. В точке с координатой 3/4Н скорость уже не равна нулю (рис. 1.6). Поэтому рассмотрим участок длиной 1/4Н. Время движения на этом участке (t- Δt). Следовательно:
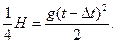(2)
Полученная система уравнений (1) и (2) является решаемой. Подставляем уравнение (1) в уравнение (2):
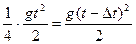
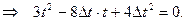
Решаем полученное квадратное уравнение относительно времени t:
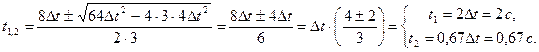
Полученный ответ t2 = 0,67 с не соответствует условию задачи, т.к. по условию задачи только на последнем участке падение длилось 1 с, следовательно, все время движения больше одной секунды. Поэтому время t1 = = 2 с является ответом. Подставляя это значение времени в уравнение (1), получим:
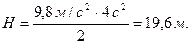
Задача 4. Определить путь, пройденный свободно падающим телом за первую 0,1 с и последнюю 0,1 с падения, если тело падает с высоты Н = 100 м.
|
|
|
Решение
1) Путь, пройденный свободно падающим телом за первую 0,1 с, находим по уравнению (1) из предыдущей задачи: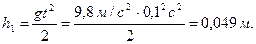 
2) Чтобы найти путь, пройденный свободно падающим телом за последнюю 0,1 с, находим все время движения: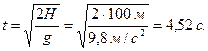 
3) Путь, пройденный свободно падающим телом за последнюю 0,1 с будет равен разности всего пути и пути, пройденного свободно падающим телом за время Δt = (4,52 с – 0,1 с) = 4,42 с:
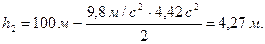
Вопросы и задания для самоконтроля
1. Что изучает механика? Рассмотрите историю создания механики и составьте свою схему взаимосвязи ее разделов.
2. Охарактеризуйте основные понятия механики. Какие свойства пространства и времени приводят в механике к законам сохранения?
3. Что изучает кинематика? Какие условия использования кинематических уравнений Вы знаете? Приведите примеры поступательного, вращательного и вращательно-поступательного движения тел.
4. Как выбирается система координат для описания механического движения?
5. Дайте определение радиус-вектора. Как определить его длину? Какие существуют два способа описания механического движения в декартовой системе координат? В чем они заключаются? Как они взаимосвязаны между собой?
6. Какое движение называется равномерным? Приведите примеры равномерного движения. Запишите системы уравнений, описывающих равномерное движение в векторном, координатном и скалярном видах. Дайте определение средней и мгновенной скорости.
7. Какое движение называется равноускоренным? Приведите примеры равноускоренного движения. Дайте определение среднего и мгновенного ускорения. Запишите системы уравнений, описывающих равноускоренное движение в векторном и координатном видах.
8. Запишите систему уравнений, описывающую равноускоренное движение в скалярном виде. Получите из нее зависимости: 1) между скоростью, ускорением и пройденным путем при равноускоренном и равнозамедленном движении; 2) между начальной и конечной скоростью, временем движения и пройденным путем при равноускоренном и равнозамедленном движении.
9.
 |
По графику зависимости ускорения а(t) от времени построить графики зависимости скорости V(t) и координаты Х(t) от времени. Считать, что начальные значения скорости V0 = 0 и координаты Х0 = 0 – заданы.
Рекомендованная литература
1. Волькенштейн В.С. Сборник задач по общему курсу. – М.: Главная ред. физ.-мат. литературы, 1987. – 456 с. – (Задачи №№ 1.1-1.25).
2. Евграфова Н.Н., В.Л. Каган. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 8-34.
3. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 11-48.
КИНЕМАТИКА ДВИЖЕНИЯ ПО ОКРУЖНОСТИ.
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
План
1 Вращательное движение. Угловые величины.
2 Взаимосвязь между линейными и угловыми величинами.
3 Система кинематических уравнений, описывающих равнопеременное движение по окружности.
4 Система кинематических уравнений, описывающих движение тела, брошенного под углом к горизонту.
5 Примеры решения задач.
1 Вращательное движение. Угловые величины
К XIV веку относятся сведения про ввод в научную терминологию понятия угловой скорости.
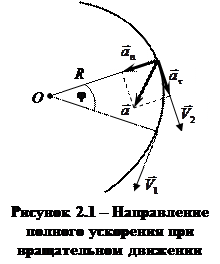
Т.к. при движении по окружности вектор скорости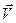 
постоянно меняет свое направление (рис.2.1), то говорить о равномерном движении по окружности некорректно.
Для описания движения по окружности полное ускорение раскладывается по правилу параллелограмма на составляющие, а его модуль рассчитывается по теореме Пифагора:
,
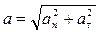где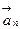 
– нормальное ускорение (центростремительное), 
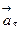– тангенциальное (касательное) ускорение.
Нормальное ускорение характеризует изменение скорости по направлению и равно отношению квадрату скорости к радиусу кривизны:
|
|
|
.
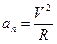Тангенциальное ускорение характеризует изменение скорости по величине и равно изменению скорости в единицу времени или равно первой производной линейной скорости по времени:
.
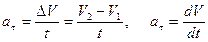При вращательном движении вводятся угловые величины, аналогичные величинам, характеризующим поступательное движение: угол поворота, угловая скорость, угловое ускорение.
Угол поворота определяется как вектор по правилу правого винта (рис. 2.2). Скалярное значение угла поворота в Системе интернациональной измеряется в радианах: φ = [рад].
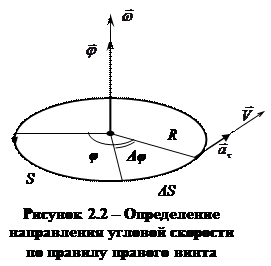Угловая скорость характеризует угол поворота в единицу времени:
.
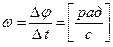Различают среднюю и мгновенную угловую скорость. Средняя угловая скорость численно равна отношению полного угла поворота ко времени, в течение которого это вращение произошло:
.
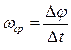Мгновенная угловая скорость определяется как предел отношения бесконечно малого угла поворота к бесконечно малому промежутку времени, в течение которого это вращение произошло, илиравна первой производной угла поворота по времени:
.
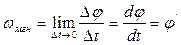Угловое ускорение численно равно изменению угловой скорости в единицу времени:
.
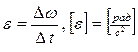Различают мгновенное и среднее угловое ускорение.
Среднее угловое ускорение равно отношению изменению угловой скорости ко времени, в течение которого это изменение угловой скорости произошло:
.
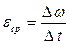Мгновенное угловое ускорение определяется как предел отношения бесконечно малого изменения угловой скорости к бесконечно малому промежутку времени, в течение которого это изменение угловой скорости произошло, т.е. равно первой производной угловой скорости по времени или второй производной угла поворота по времени:
.
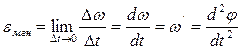2 Взаимосвязь между линейными и угловыми величинами
Взаимосвязь между углом поворота и длиной дуги окружности (рис. 2.2):
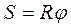, (2.1)
где S –длина дуги, R – радиус кривизны траектории, j – угол поворота [ j ] = [ рад ].
Дифференцируем уравнение (2.1) по времени dt: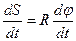 
.
После интегрирования получим взаимосвязь между линейной и угловой скоростями: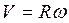 
. (2.2)
|
|
|
Продифференцируем уравнение (2.2) по времени dt: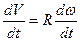 
.
После интегрирования получим взаимосвязь между тангенциальным и угловым ускорением:
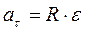. (2.3)
3 Система кинематических уравнений, описывающих равнопеременное движение по окружности
Угол поворота и угловую скорость можно определить как интегралы:
, 
.
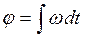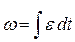Решение этих уравнений приводит к системе уравнений, описывающих равнопеременное движение по окружности:
.
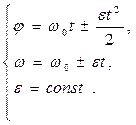Для решения задач с использованием данной системы уравнений необходимо использование дополнительных формул.
Пусть N – полное число оборотов, тогда полный угол поворота буде равен:
.
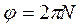Если T – период вращения (время одного полного оборота), тогда частота вращения n определяется по формуле:
.
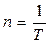А угловая скорость определяется по формулам:
, 
.
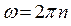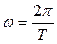4 Система кинематических уравнений, описывающих движение тела, брошенного под углом к горизонту
Из истории науки. Решение задачи на движение тел, брошенных под углом к горизонту (рис. 2.3), стало актуальным задачи, когда в XIV веке в Европе появился порох. Порох был изобретен в Китае в ІХ веке для красочных фейерверков. Тогда китайцы не знали, что стали первыми изобретателями взрывчатки. В 1866 г. шведский химик Альфред Нобель изобрел динамит. Потом он создал другие виды взрывчатого вещества, в том числе гелигинит. Взрывчатку используют как в мирных целях (снесение препятствий и сооружений, строительство шахт и тому подобное), так и против жизни человека. Взрывчатые вещества используются в бомбах, ракетах и других видах оружия. В то же время взрывчатые вещества используются для фейерверков и салютов. Мы все видели на открытии ХХ зимних Олимпийских игр в Турине цветные фейерверки при зажигании олимпийского огня. Красивейшее зрелище представляют собой салюты в честь самого для нас священного праздника – дня Победы.
 |
Леонардо да Винчи (1452-1528) много времени уделял изучению траектории полета стрелы и ядра, что было очень важно для развития военной техники того времени. Он, практически незнающий математики, исследовал зависимость дальности полета от выталкивающей силы взрывчатого вещества. Закончили решение этой задачи Н. Тартальи и Г. Галилей.
Математики и механики Европы того времени начали решать эту задачу о том, как угодить в цель. В XVI веке итальянский математик Н. Тарталья (1499-1557) в трактатах «Новая наука» (1537) и «Проблемы и различные изобретения» (1546) описал траекторию движения снарядов, доказал, что она криволинейна и наибольшая дальность полета достигается при наклоне ствола пушки под углом 45о к горизонту, чем положил начало баллистике.
В 1604-1609 годах г. Падуя, где жил и работал Г. Галилей, принадлежала Венецианской республике, и ученый поддерживал постоянные контакты с венецианским арсеналом. В это время Г. Галилей установил законы движения тела, брошенного под углом к горизонту. Он показал, что движение под углом к горизонту, складывается из равномерного прямолинейного движения, которое имело бы место при отсутствии силы тяжести, и свободного падения, что образует параболическую траекторию. А далее, пользуясь свойствами параболы, Г. Галилей составил «таблицу для стрельбы», имеющую важное практическое значение. Этим самым Г. Галилей положил начало новой науке – баллистике.
Также Г. Галилей доказал утверждение Н. Тартальи о том, что угол 45о отвечает наибольшей дальности полета, и показал, что для углов, дающих в сумме 90о, дальности полета одинаковы (при фиксированной величине скорости).
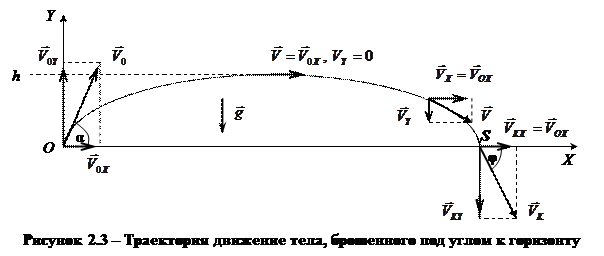
Рассмотрим траекторию движения тела, брошенного под углом к горизонту (рис. 2.3). Перемещение тела, брошенного под углом к горизонту, можно разложить на два: горизонтальное и вертикальное. Именно поэтому изобразим направление вектора скорости в различных точках траектории и, используя правило параллелограмма, разложим его на составляющие, параллельные осям OX и OY, как это сделал Г. Галилей.
Проекции вектора скорости на оси OX и OY равны:
,
.
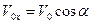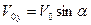Так как относительно оси OX вектор скорости не меняет своего направления, то относительно этой оси тело движется равномерно, т.е. подчиняется законам равномерного движения:
,
.
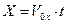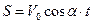Так как относительно оси OY вектор скорости изменяется, как и при движении свободного падения, то движение тела относительно оси OY подчиняется законам свободного падения:
,
,
.
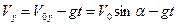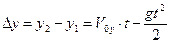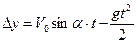Скорость тела в любой момент времени определяется по формуле (рис. 2.3):
.
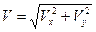Угол, под которым тело падает на землю, определяется из соотношения:
.
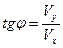Полное ускорение определяется теоремой Пифагора (рис. 2.4):
 |
.
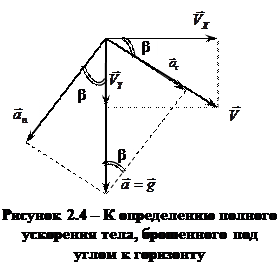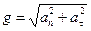5 Примеры решения задач
Задача 1. Мяч бросили со скоростью V0 под углом α к горизонту. Сколько времени t мяч будет находиться в воздухе? На какую высоту h мяч поднимется? На каком расстоянии S от места бросания мяч упадет?
 |
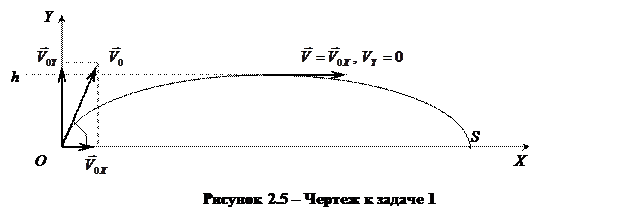Решение
1) Рассмотрим перемещение тела, брошенного под углом к горизонту, в горизонтальном и вертикальном направлении. Найдем время полета мяча t. Из чертежа к задаче (рис. 2.5) видно, что координата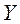 
за все время движения не изменилась, т.е.: 
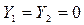. Следовательно, используя формулу 
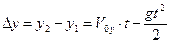, получим выражение для определения времени движения тела:
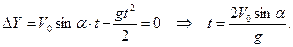
2) Определим, на каком расстоянии S от места бросания мяч упадет на землю. Для этого в формулу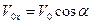 
подставим полученное выражение для времени:
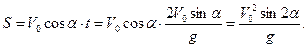
3) Высоты h мяч достигнет через время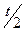 
. Тогда:
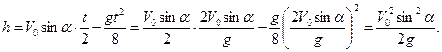
Задача 2. Тело, брошенное горизонтально, упало на землю через время t на расстоянии S от места бросания. С какой высоты h кинули тело? Определить начальную V0 и конечную V скорости тела. Какой угол φ составляет траектория тела с горизонтом в точке падения?
Решение
1) Перемещение тела, брошенного горизонтально, разложим на два: горизонтальное и вертикальное (рис. 2.6).
2) Проекция начальной скорости на ось OY равна нулю, т.к. вектор начальной скорости перпендикулярен оси OY: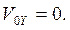 
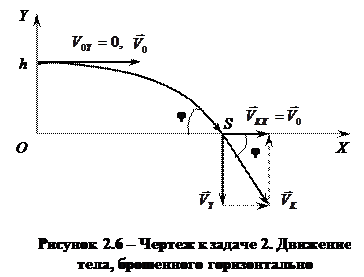Начальная координата Y1 = h, конечная координата Y2 = 0. Следовательно:
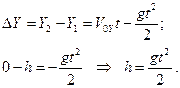
3) Относительно оси OХ движение равномерное. Поэтому относительно оси OХ:
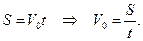
4) Конечную скорость находят по формуле для определения полной скорости в любой момент времени: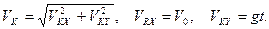 
Тогда: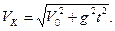 
4) Из чертежа к задаче (рис. 2.6) видно, что угол φ, который составляет траектория тела с горизонтом в точке падения, будет равен: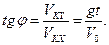 
Задача 3. По интегральной зависимости между углом поворота и угловой скоростью и между угловой скоростью и угловым ускорением получить систему уравнений, описывающих равнопеременное движение по окружности. Сравнить полученную систему с системой уравнений, описывающих поступательное равноускоренное движение.
Решение
По определению угловая скорость равна первообразной от углового ускорения: 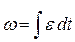. Проинтегрируем это выражение и получим:
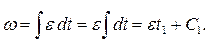
В момент времени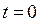 
угловая скорость равна 
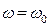– начальному значению. Следовательно, постоянная интегрирования С1 принимает значение начальной угловой скорости: 
.
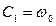Тогда получаем зависимость угловой скорости от времени:
.
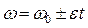По определению угол поворота равен первообразной от угловой скорости: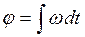 
. Проинтегрируем это выражение и получим:
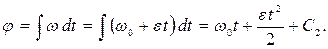
В момент времени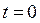 
угол поворота равен 
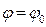– начальному значению. Следовательно, постоянная интегрирования С2 принимает значение начального значения угла поворота: 
.
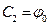Таким образом, получаем зависимость угла поворота от времени:
.
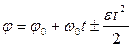Окончательно получаем систему уравнений, описывающих равноускоренное движение по окружности:
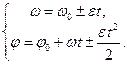
Сравнивая полученную систему с системой уравнений, описывающих поступательное равноускоренное движение:
,
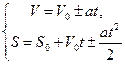можно сделать вывод об универсальности системы уравнений для любых видов равноускоренного движения. Т.е. законы, описывающие равноускоренное движение, симметричны.
Вопросы и задания для самоконтроля
1. Рассмотрите историю изучения законов кинематики равноускоренного движения. Составьте схему-последовательность появления основных понятий кинетики.
2. Обоснуйте использование в научных исследованиях метода физического сравнения. Какие сравнения Вы сделали в этой лекции?
3. Почему движение по окружности с постоянной по модулю скоростью некорректно называть равномерным?
4. Какие виды ускорений вводятся для описания движения по окружности? Что они характеризуют?
5. Дайте определение средней и мгновенной угловой скорости.
6. Дайте определение среднего и мгновенного углового ускорения.
7. Какую взаимосвязь между углом поворота и длиной дуги окружности мы используем для вывода взаимосвязи между линейными и угловыми величинами?
8. Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением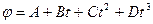 
, где В = 1 рад/ с, С = 1 рад /с2, D = 1 рад /с3. Определить для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение, 2) нормальное ускорение, 3) полное ускорение.
9. Запишите систему уравнений, описывающую равноускоренное движение по окружности. Получите из нее зависимости: 1) между угловой скоростью, угловым ускорением и углом поворота при равноускоренном и равнозамедленном движении; 2) между начальной и конечной угловой скоростью, временем движения и углом поворота при равноускоренном и равнозамедленном движении.
10. Какие физические величины называются: периодом вращения? частотой вращения? Какая между ними существует взаимосвязь? Как они связаны с угловой скоростью?
11. 
Объясните, какие рассуждения позволяют нам рассматривать сложную траекторию движения тела, брошенного под углом к горизонту, отдельно относительно осей OX и OY.
12. Крепость Ени-Кале (рис. 2.6) построена в XVIII веке в Керчи в районе самого узкого места (4,2 км) между Крымом и Кубанью на берегу Керченского пролива с целью обороны крымского берега. Под каким углом к горизонту должны были вылетать ядра из пушек, чтобы можно было простреливать весь пролив поперек? Начальная скорость ядер достигала 150 м/с.
Рекомендованная литература
1. Волькенштейн В.С. Сборник задач по общему курсу. – М.: Главная ред. физ.-мат. литературы, 1987. – 456 с. – (Задачи №№ 1.26-1.64).
2. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 35-47.
3. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 44-48; 60-68.
4. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1990. – 478 с. – С. 12-13.
5. Храмов Ю.А. Биография физики: Хронологический справочник. – К.: Техника, 1983. – 344 с. – С. 5-19; 55-77.
ДИНАМИКА
План
1. Основные понятия динамики.
2. Первый закон Ньютона.
3. Второй закон Ньютона.
4. Третий закон Ньютона.
5. Виды сил в природе. Сила всемирного тяготения.
6. Силы упругости.
7. Сила тяжести.
8. Вес тела.
9. Силы реакции.
10. Силы трения.
11. Принцип относительности Галилея. Закон сложения скоростей.
12. Примеры решения задач.
Из истории науки. Развитие производственных отношений в странах Западной и Центральной Европы в XV-XVI вв. стало толчком к быстрому развитию ремесел, торговли, мореплавания, военного дела, а также выдающихся астрономических открытий. Это привело к развитию динамики. Систематизация и обобщение накопленных человеком знаний привели к определению законов динамики Галилео Галилеем (1564-1642) и Исааком Ньютоном (1643-1727), которые И. Ньютон систематизировал и обобщил в «Математических началах натуральной философии» (1687). В своем исследовании И. Ньютон сформулировал основные понятия (масса, количество движения, сила), принципы и законы классической механики.
В настоящее время основные законы классической механики И. Ньютона используются инженерами и физиками практически без изменений. Как И. Ньютон, так и современные ученые, считают, что прямой задачей механики является определение ускорения по силам, действующим на тело, а обратной задачей – определение равнодействующей сил по ускорению тела.
1 Основные понятия динамики
Динамика – раздел механики, изучающий законы механического движения с учетом причин, вызывающих это движение (сила – причина изменения поступательного движения, момент силы – вращательного движения).
Сила – физическая величина, являющаяся количественной мерой взаимодействия тел. В Системе интернациональной сила измеряется в Ньютонах:
.
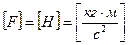Сила – векторная величина, а это значит, что она имеет точку приложения, направление и абсолютное значение (модуль). Например, сила тяжести (рис. 3.1): т. О – центр тяжести тела – точка приложения силы тяжести; вектор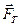 
показывает направление силы тяжести; модуль силы тяжести равен: 
.
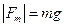Векторную сумму сил можно рассматривать как принцип суперпозиции сил. Векторная сумма сил, действующих на тело, называется равнодействующей:
.
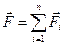Законы динамики являются обобщением экспериментальных фактов. Законы Ньютона являются ядром всей механики. Из них можно получить другие законы механики.
2 Первый закон Ньютона
Существуют такие системы отсчета, относительно которых тела сохраняют состояния покоя или равномерного прямолинейного движения, если на них не действуют никакие другие тела или действие этих сил скомпенсировано. Такие системы отсчета называются инерциальными.
Из І закона Ньютона следует, что инерциальные системы отсчета могут двигаться только равномерно и прямолинейно.
Системы отсчета, двигающиеся с ускорением, называются неинерциальными. В неинерциальных системах отсчета движение тел осложнено действием сил инерции.
3 Второй закон Ньютона
ІІ закон Ньютона: Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально массе тела:
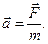
Подставим определение ускорения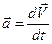 
в это уравнение:
,
.
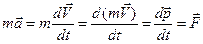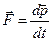Следовательно,равнодействующая, равна первой производной импульса по времени. Именно так, через импульс, И. Ньютон сформулировал II закона в «Математических началах натуральной философии» (1687).
4 Третий закон Ньютона
Все тела взаимодействуют с силами, равными по величине и противо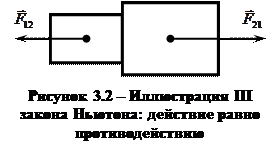 
положными по направлению (действие равно противодействию).
ІІІ закон Ньютона записывают как в векторном, так и в скалярном виде (рис.3.2).
ІІІ закон Ньютона в векторном виде:
.
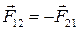ІІІ закон Ньютона в скалярном виде:
.
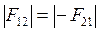5 Виды сил в природе. Сила всемирного тяготения
В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения.
Этот закон был открыт И. Ньютоном в 1666 г. для точечных или симметричных сферических масс: два тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между их центрами:
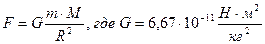– гравитационная постоянная.
Сила всемирного тяготения создается всеми телами, имеющими массы. Силы притяжения между телами направлены по линии, соединяющей центры этих тел. Поэтому сила всемирного тяготения является центральной.
Ускорение свободного падения на поверхности любой планеты определяют из рассуждений, что вблизи планеты или на ее поверхности сила тяжести и сила всемирного тяготения равны:
.
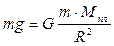Таким образом, ускорение свободного падения на поверхности планеты определяется по формуле:
.
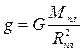Из истории науки. Сама идея всеобщей силы тяготения неоднократно высказывалась и до И.Ньютона. Ранее о ней размышляли Эпикур (342-271 гг. до н.э.), П.Гассенди (1592-1655), Д.А. Борелли(1608-1679), И. Кеплер (1571-1630), Р.Декарт (1596-1650), Х.Гюйгенс (1629-1695) и др. И. Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики. Р. Декарт считал его результатом вихрей в эфире. Были догадки с правильной зависимостью от расстояния. И. Ньютон в письме к Г. Галлею упоминает своих предшественников, в том числе и Р. Гука. Но до него никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера).
В 1687 г. в «Математических началах натуральной философии» И. Ньютон вывел закон тяготения, основываясь на эмпирических законах И. Кеплера, известных к тому времени. Он показал, что наблюдаемые движения планет свидетельствуют о наличии центральной силы. Обратно, центральная сила притяжения приводит к эллиптическим (или гиперболическим) орбитам.
Теория И. Ньютона, в отличие от гипотез предшественников, имела ряд существенных отличий. Он опубликовал не просто предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:
· закон тяготения;
· закон движения (второй закон Ньютона);
· система методов для математического исследования (математический анализ).
В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел, тем самым создавая основы небесной механики. До А. Эйнштейна никаких принципиальных поправок к указанной модели не понадобилось, хотя оказалось необходимым значительно развить математический аппарат.
Теория тяготения Ньютона уже не была гелиоцентрической. Уже в задаче двух тел планета вращается не вокруг Солнца, а вокруг общего центра тяжести, так как не только Солнце притягивает планету, но и планета притягивает Солнце. Наконец, выяснилась необходимость учесть влияние планет друг на друга.
Со временем оказалось, что закон всемирного тяготения позволяет с огромной точностью объяснить и предсказать движения небесных тел, и он стал рассматриваться как фундаментальный. В то же время ньютоновская теория содержала ряд трудностей. Главная из них – необъяснимое дальнодействие: сила притяжения передавалась непонятно как через совершенно пустое пространство, причём бесконечно быстро. По существу ньютоновская модель была чисто математической, без какого-либо физического содержания. Кроме того, если Вселенная, как тогда предполагали, евклидова и бесконечна, и при этом средняя плотность вещества в ней ненулевая, то возникает гравитационный парадокс. В конце XIX века обнаружилась ещё одна проблема: расхождение теоретического и наблюдаемого смещения перигелия Меркурия.
6 Силы упругости
Из истории науки. В 1657 г. Роберт Гук (1635-1703) экспериментально открыл основной закон упругости твердых тел, выражающий зависимость между напряженным состоянием и деформацией упругого тела (для простейшего случая растяжения (сжатия) стержня). А в 1807 году Т. Юнг (1773-1829) впервые ввел понятие модуля упругости.
Силы упругости возникают при изменении формы или объема тел, т.е. при деформациях, под действием внешней силы. Следует различать слабое и сильное воздействие на тело.
После снятия сильных воздействий в теле остаются необратимые изменения формы или объема. Такой вид деформации называют пластической.
При малых воздействиях (упругих деформациях) справедлив закон Гука:
Деформация тела прямо пропорциональна силовому воздействию на тело (механическому напряжению) и после снятия нагрузок тело принимает свою первоначальную форму и размеры.
Частные случаи закона Гука
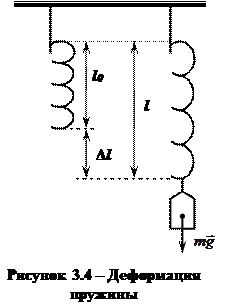
1 При деформации пружин сила упругости прямо пропорциональна абсолютному удлинению: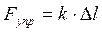 
, где Δ l – абсолютное удлинение (рис. 3.4), [ м ]; k – коэффициент жесткости (упругости) пружины, [ Н/м ].
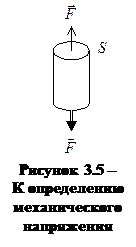2 При деформации сжатия-растяжения сплошных твердых тел характеристикой силового воздействия является механическое напряжение – физическая величина, характеризующая силу, действующую на единицу площади поперечного сечения тела (рис. 3.5):
.
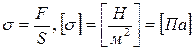Характеристикой деформации в случае деформации сжатия-растяжения (рис. 3.4) является относительное удлинение, показывающее степень или долю удлинения:
.
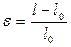Закон Гука:При малых деформациях сплошных твердых тел механическое напряжение пропорционально относительному удлинению:
,
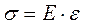где σ – механическое напряжение, ε – относительное удлинение, [ E ] = [ Па ] – модуль Юнга, характеризует упругие свойства твердых тел.
Деформация растяжения возникает тогда, когда на стержень, трос, пружину и т.д. действуют внешние силы, приложенные к их концам, направленные в разные стороны и совпадающие с продольной осью этих тел.
При этом наблюдается не только удлинение тела, но и уменьшение площади его поперечного сечения.
3 При деформации сдвига характеристикой силового воздействия является касательное напряжение – физическая величина, характеризующая силу, касательную к поверхности и действующую на единицу этой поверхности:
.
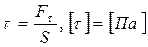Характеристикой деформации при деформации сдвига (рис. 3.6, 3.7) является угол сдвига γ, [ γ ] = [ рад ].
Закон Гука: При деформации сдвига касательное напряжение прямо пропорционально углу сдвига:
,
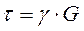где τ – касательное напряжение, [ G ] = [ Па ] – модуль сдвига, характеризует упругие свойства материала.
Сдвиг – вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно). Следует иметь в виду, что в конструкциях этого вида деформации не бывает в чистом виде. Например, в заклепочном соединении пренебрегают изгибом и растяжением стержня заклепки.
 |
4 При деформациях кручения характеристикой силового воздействия является момент силы:
.
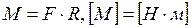Характеристикой деформации в случае деформации кручения (рис. 3.8, 3.9) является угол кручения φ, [ φ ]=[ рад ].
Закон Гука: При деформации кручения момент силы прямо пропорционален углу кручения:
,
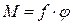где f – модуль кручения, характеризующий упругие свойства материала и зависящий от размеров и формы. Например, для цилиндра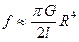 
, где G – модуль сдвига.
Брус круглого поперечного сечения подвергается деформации кручения. В металлообрабатывающих станках деформации кручения подвергается так называемый трансмиссионный вал с насаженными на него шкивами ременных передач. Трансмиссионными называют валы, назначение которых состоит в получении мощности от двигателя и передаче ее рабочим машинам.
7 Сила тяжести
Сила тяжести – это сила, действующая на любую материальную частицу, находящуюся вблизи земной поверхности. Сила тяжести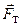 
определяется как геометрическая сумма силы притяжения Земли 
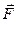и центробежной силы инерции 
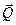, учитывающей эффект суточного вращения Земли. Сила тяжести определяется формулой:
.
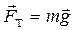Вектор силы тяжести имеет точку приложения в центре тяжести тела (т. О) и направлен по вертикали вниз.
 |
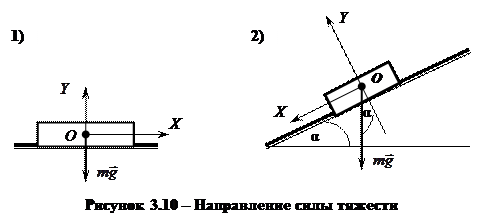При решении задач определяют проекции силы тяжести на оси OX и OY (рис. 3.10):
| 1) | OX:  ,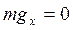
| 2) | OX:  ,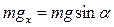
|
OY:  .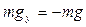
| OY:  .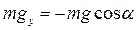
|
8 Вес тела
Вес тела – это сила воздействия тела на опору (или другой вид крепления в случае подвешенных тел), возникающая в поле сил тяжести. При движении опоры или подвеса с ускорением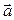 
вес тела определяется соотношением:
.
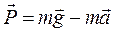В случае если тело будет двигаться вниз с ускорением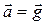 
, вес тела становится равным нулю (
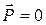). Такое состояние тела, при котором его вес становится равным нулю, называется невесомостью.
9 Силы реакции
При соприкосновении тел, эти тела могут деформироваться. Часто эти деформации могут быть чрезвычайно малыми, но, тем не менее, они приводят к возникновению сил упругости, которые в этом случае называются силами реакции.
Силы реакции– силы, возникающие в местах контактов тел. Как и все силы упругости, силы реакции направлены в сторону, противоположную возникшим деформациям.
Если два тела могут скользить одно по поверхности другого без трения, то такие тела называют гладкими. Для гладких поверхностей сила их взаимодействия направлена перпендикулярно поверхности их соприкосновения и называется силой нормальной реакции. Таким образом, в физике силы реакции, как один из видов сил упругости, направляют в сторону, противоположную деформации.
Силами реакции моделируют влияние других тел на исследуемое тело. Не существует аналитических выражений, определяющих силу реакции. Для этого необходимо рассчитать деформации каждого тела, приводящие к возникновению равновесных сил упругости. В связи с этим при решении различных задач, силы реакции находят из условий равновесия или законов движения тел.
 |
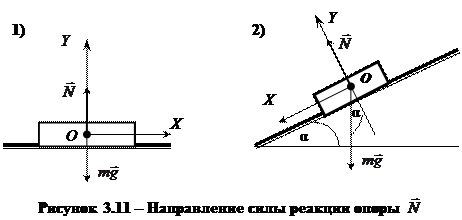Разделяют реакции опоры (рис. 3.11) и силы реакции нити (рис. 3.12).
При решении задач определяют проекции сил реакции OX и OY.
v Для сил реакции опоры (рис. 3.11):
| 1) | OX:  ,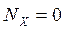
| 2) | OX:  ,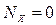
|
OY:  .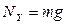
| OY:  .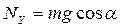
|
 |
v Для сил реакции нити (рис. 3.12):
| 3) | OX:  ,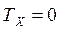
| 4) | OX:  ,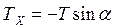
|
OY:  .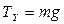
| OY:  .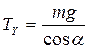
|
10 Силы трения
Трение – процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии.
Силы трения – силы, возникающие в местах контактов тел при относительном сдвиге или скольжении.
Различают силы трения покоя, скольжения, качения, вязкого трения.
Сила трения покоя – сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения. Из графика зависимости силы трения скольжения от действия внешних сил (рис. 3.13) видно, что сила трения покоя изменяется в пределах от нуля до величины силы трения скольжения, т.е.:
,
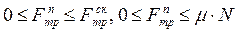где μ – коэффициент трения скольжения (зависит от материала, качества обработки, смазки).
Сила трения скольжения – сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
Величина силы трения скольжения определяется формулой (рис. 3.13):
.
  |
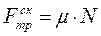Таким образом, можно сделать вывод о том. Что максимальная сила трения покоя и сила трения скольжения прямо пропорциональны коэффициенту трения скольжения и силе реакции.
Рассмотрим примеры определения максимальной силы трения покоя или силы трения скольжения для случаев, изображенных на рисунке 3.14.
 |
Для этого найдем проекции сил реакции на ось OY и полученные значения подставим в формулу для определения силы трения скольжения:
| 1) | OY:  ,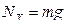
| 2) | OY:  ,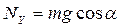
|
  .
|  .
|
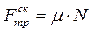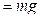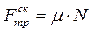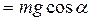Трение качения – это явление сопротивления движению, возникающее при перекатывании тел. Проявляется, например, между элементами подшипников качения, между шиной колеса автомобиля и дорожным полотном. В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике.
Сила трения качения возникает при качении тел за счет деформации тел. Физический механизм формирования этих сил (рис. 3.15) связан с деформацией тел в точке качения и наклоном полной силы реакции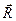 
под углом k к вертикали. Горизонтальная составляющая полной силы реакции и есть сила трения качения 
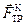при условии, что скорость тела 
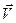направлена в противоположную сторону.
Сила трения качения определяет закон Амонтона-Кулона:
,
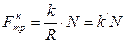где R – радиус катящегося тела,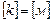 
– коэффициент трения качения, 
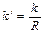– безразмерный коэффициент трения качения.
Типичные значения коэффициентов трения скольжения и трения качения лежат в пределах: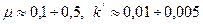 
. Таким их отличием объясняется исторический переход от трения скольжения (сани и др.) к трению качения во многих технических устройствах (колесо, подшипники и др.) и живых организмах (суставы, пешая ходьба и др.).
Силы вязкого трения возникают при движении тел в жидкостях и газах. Величина силы вязкого трения в зависимости от скорости принимает значения:
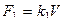– при малых скоростях,
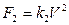– при больших скоростях,
где k1 и k2 – коэффициенты вязкого трения, зависящие от плотности жидкости или газа, формы, размеров тела и т.д.
Большие и малые скорости (в случае вязкого трения) являются понятиями относительными, поэтому выбираются в зависимости от конкретных условий исследуемого явления или задачи.
Из истории науки. В 1850 году английский физик-теоретик и математик ирландского происхождения Дж. Стокс (1819-1903) установил закон, определяющий силу сопротивления, испытываемую твердым шаром радиуса r при его движении с малыми скоростями V (сила Стокса):
,
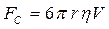где η – динамическая вязкость. В СИ измеряется в [ η ] = [ кг/м∙с ]= [ Н∙с/м2 ].
11 Принцип относительности Галилея. Закон сложения скоростей
 |
Относительность движения заключается в том, что некоторые характеристики движения (скорость, форма траектории) имеют различные значения в различных системах отсчета. На рис. 3.16: X,Y,Z – неподвижная система отсчета, X’,Y’,Z’ – подвижная система отсчета. Пусть подвижная система отсчета движется со скоростью 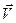, а самолет со скоростью 
.
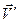По правилу треугольника сложения векторов радиус-векторы тела в подвижной и неподвижной системах координат связаны соотношением:
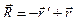, следовательно 
.
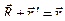Дифференцируя полученное выражение по времени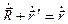 
, получим закон сложения скоростей:
,
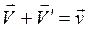где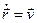 
– скорость тела относительно неподвижной системы отсчета, 
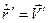– скорость тела относительно подвижной системы отсчета, 
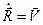– скорость подвижной системы отсчета относительно неподвижной.
Таким образом, можно сформулироватьзакон сложения скоростей: скорость тела в подвижной системе отсчета относительно неподвижной равна сумме скоростей тел в подвижной системе отсчета и скорости самой подвижной системы отсчета относительно неподвижной.
Дифференцируя по времени формулу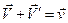 
, получим: 
.
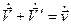Для инерциальной системы отсчета V=const (т.к. ускорение равно нулю), следовательно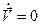 
.
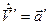, где 
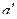– ускорение тела относительно подвижной системы координат.
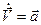, где 
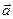– ускорение тела относительно неподвижной системы координат.
Окончательно получаемпринцип относительности Галилея – ускорение тела в подвижной и неподвижной системах отсчета одинаково:
.
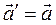Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.
Экспериментально установлено, что при малых скоростях массы тел и силы также одинаковы во всех инерциальных системах отсчета. Поэтому справедлив принцип относительности Галилея – фундаментальный физический принцип, согласно которому законы Ньютона имеют одинаковую форму во всех инерциальных системах отсчета.
Таким образом, все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Иллюстрацией этого утверждения может служить рис. 3.17, на котором изображено движение тела под действием силы тяжести. Центр масс тела движется по параболической траектории как материальная точка, в то время как все другие точки движутся по более сложным траекториям.
Из истории науки. Отцом принципа относительности считается Галилео Галилей, который обратил внимание на то, что находясь в замкнутой физической системе, невозможно определить, покоится эта система или равномерно движется. Во времена Галилея люди имели дело в основном с чисто механическими явлениями. В своей книге «Диалоги о двух системах мира» Галилей сформулировал принцип относительности следующим образом: «Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет своё действие только на вещах, не принимающих в нём участия». Идеи Г.Галилея нашли развитие в механике И.Ньютона. В своих «Началах» (том I, следствие V) И. Ньютон так сформулировал принцип относительности: «Относительные движения друг по отношению к другу тел, заключенных в каком-либо пространстве, одинаковы, покоится ли это пространство, или движется равномерно и прямолинейно без вращения».
Различают принцип относительности Эйнштейна (для скоростей, сравнимых со скоростью света) и принцип относительности Галилея (для законов классической механики).
