Теория рычага Архимеда

Архимед сделал много открытий в математике, гидростатике, заложил основу механики как новой науки. Особый его интерес привлекала задача о рычаге. В сочинении «О рычагах» им были установлены правила сложения и разложения параллельных сил, дано определение понятия центра тяжести системы двух грузов, подвешенных к стержню, и выяснены условия равновесия такой системы. Архимеду же принадлежит открытие основных законов гидростатики. Свои теоретические знания в области механики он применял к различным практическим вопросам строительства и военной техники, конструкции которой, основываясь на рычаге, позволяла перемещать в пространстве тела большого веса при относительно небольших усилиях.

В дальнейшей истории технической культуры механика рассматривалась как наука о простых статических машинах. Ее основой стала теория рычага, изложенная Архимедом в сочинениях «О равновесии плоских тел и центрах тяжести плоских фигур» и не дошедшим до нас «О весах». В основе этой теории лежат следующие постулаты:

v равные тяжести на равных длинах уравновешиваются, на неравных же длинах не уравновешиваются, но перевешивает тяжесть на большей длине;

v если при равновесии тяжестей на каких-нибудь длинах к одной из тяжестей будет что-то прибавлено, то они не будут уравновешиваться, но перевесит та тяжесть, к которой было прибавлено;

v точно так же, если от одной из тяжестей будет отнято что-нибудь, то они не будут уравновешиваться, но перевесит та тяжесть, от которой не было отнято;

v если две величины уравновешиваются на каких-нибудь длинах, то на тех же самых длинах будут уравновешиваться и равные им.

Не подлежит сомнению, что постулаты проверены длительной технической практикой, которая делает их «очевидными». Основываясь на этих постулатах, Архимед формулирует закон рычага и доказывает следующие теоремы:

1 Соизмеримые величины уравновешиваются на длинах, обратно пропорциональных тяжестям.

2 Если величины несоизмеримы, то они точно так же уравновесятся на рычагах, которые обратно пропорциональны этим величинам.

В трактате «Механические проблемы» Архимед описал принципы действия рычага, колодезного журавля с противовесом, равноплечих весов, равноплечих весов – безмен, клещей, топора, кривошипа, вала, колеса, катка, полиспаста – механизма с несколько подвижных и неподвижных блоков, гончарного круга, руля и т.д. Но главной темой трактата является принцип рычага и определение центра тяжести тела. Свои открытия и изобретения он практически применял в различных военных машинах и механизмах (орудиях, поворотных кранах, железных лапах, поднимали вверх нос корабля противника и ставили его вертикально и т.д.) для защиты его города – Сиракуз.

Еще со времен Архимеда главной задачей статики считается установление условий равновесия данной системы сил, сложения сил и представление системы сил, действующих на тело, в простейшем виде.

Примеры решения задач

Задача 1. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Коэффициент трения между телом и плоскостью равен μ. При каком значении силы F движение будет равномерным?

Решение

1) Изобразив на чертеже к задаче (рис. 7.6) все силы, действующие на тело, записываем уравнение равновесия в векторном виде:

(1.1)

2) Записываем условие равновесия в проекциях на оси:

По определению силы трения скольжения:

Полученное значение силы трения подставляем в уравнение (1.3) и находим значение силы F:

Задача 2. Определить коэффициент трения между телом и наклонной плоскость, на которой оно покоится, если угол наклона плоскости α = 30^о.

Решение

На чертеже изображают все силы, действующие на тело (рис. 7.7) и записывают уравнение равновесия в векторном виде:

Выбираем оси координат OX и OY. Записываем уравнение равновесия в проекциях на выбранные оси:

Из уравнения (2.2) определяем силу реакции опоры:

По определению силы трения скольжения:

Полученное значение силы трения подставляем в уравнение (2.1) и коэффициент трения:

Задача 3. Определить положение центра тяжести однородной круглой пластины радиусом R = 0,5 м, в которой вырезано квадратное отверстие со стороной так, как указано на рисунке 7.8.

Решение

Относительно центра тяжести фигуры результирующий момент сил, действующих на тело, равен нулю: Если вставить вырезанную часть пластинки на прежнее место, то силу тяжести всей пластинки F_T можно представить как сумму двух параллельных сил – силы тяжести вырезанной части F_T1 и силы тяжести оставшейся фигуры F_T2:

Уравнение моментов относительно точки О будет иметь вид:

или

Из уравнения (3.1) получаем и подставляем в уравнение (3.2):

По определению силы тяжести:

где ρ – плотность материала, из которого изготовлена пластинка, S – площадь пластинки, h – ее высота, S₁ – площадь вырезанной части.

Тогда получаем выражение для положения центра тяжести однородной круглой пластины x:

где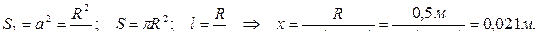

Задача 4. Как надо положить книги, чтобы составить наклонную стопку?

Решение

Стопка книг не рассыплется, если расставлять их так, чтобы центр тяжести всех книг, находящихся выше некоторой произвольно выбранной книги, лежал на вертикали, проходящей через эту книгу. Это условие должно выполняться для любой книги в стопке.

Задача 5. Постройте, как в цирке, фигуру из домино (рис. 7.9).

Решение

Если стол совершенно горизонтален и прочно стоит на полу, можно выстроить фигуру из домино. Сначала надо поставить стоймя три косточки домино, – на них возвести такую хрупкую постройку легче, чем на одной кости. Потом, когда все будет построено, осторожно убирают две крайние косточки, которые служили подпорками, и ставят их на вершину всего непрочного здания.

Равновесие здесь вполне возможно; нужно только, чтобы перпендикуляр, опущенный из центра тяжести всей конструкции, прошел через основание нижней косточки домино.

Вопросы и задания для самоконтроля

1. Что изучает статика? В чем заключается различие между динамикой и статикой? Рассмотрите историю создания статики как науки и составьте свою хронологическую таблицу ее развития.

2. Какая точка твердого тела называется центром тяжести? Как определяется центр тяжести твердого тела? Как связаны между собой центр тяжести и центр масс твердого тела?

3. Какое состояние твердого тела называется равновесием? Сформулируйте два условия равновесия. Какие виды равновесий различают? Дайте им определения и приведите примеры их проявления в природе, быту и т.д.

4. В чем заключается теория рычага великого Архимеда?

5. Какое механическое устройство называется кардановым подвесом? Нарисуйте его схему.

8. Поставьте неваляшку (Ваньку-встаньку) на шероховатую доску и слегка приподнимите один из концов доски, как это показано на рис. 7.10. Как Вы думаете, в какую сторону отклонится голова игрушки при сохранении её равновесия? Правильно ли это явление изображено на рисунке?

9. Для сохранения в неизменном положении предметов при движении их опоры уже много столетий применяется так называемый карданов подвес – устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. В качестве примера можно рассмотреть корабельную керосиновую лампу. При любой качке на море благодаря вращающемуся карданову подвесу лампа всегда сохраняет вертикальное положение. Нарисуйте схему корабельной керосиновой лампы, прикрепленной к вращающемуся карданову подвесу.

10. На рис. 7.11 изображены два положения грузовой машины. Объясните, почему на фото а машина стоит устойчиво, а на фото б – эта же машина опрокинулась.

11.

В одном случае два человека тянут за концы каната в противоположные стороны с равными силами F. В другом случае один конец каната привязан к неподвижной опоре, а за другой его конец тянут два человека с теми же силами F. Какое натяжение испытывает канат в обоих случаях?

12. Что человеку делать легче: 1) тянуть груз? 2) толкать груз? Почему? Ответ обоснуйте. По каждому из этих рисунков 7.13 составьте и решите задачи.

13. Объясните причину смешения грузов от положения равновесия в грузовом отсеке автомобиля, изображенных на рис. 7.12.

14. При взвешивании на неравноплечих весах рычажных весах масса тела (по сумме весов положенных гирь) на одной чаше весов оказалась равной 2,2 кг, а на другой – 3,8 кг. Определить истинную массу груза.

15. Тяжелый цилиндрический каток необходимо поднять на ступеньку высоты h. Определить наименьшую силу F, которую необходимо для этого приложить к центру катка в горизонтальном направлении, если каток имеет радиус R, а масса катка равна М (рис. 7.14).

16. К концам груза массой 10 кг и длиной 40 см подвешены грузы массами 40 кг и 10 кг. Где надо подпереть стержень, чтобы он находился в равновесии?

17. Масса Луны составляет 1,2 % массы Земли. Расстояние между их центрами 384000км. Где расположен центр масс системы «Земля — Луна»?

18. Объясните причину устойчивого равновесия огромной глыбы, изображенной на фото (рис. 7.16)

19. Определить положение центра тяжести однородной квадратной пластины со стороной а = 0,18 м, в которой вырезано квадратное отверстие со стороной а = 0,2 м как показано на рисунке 7.15 к задаче.

Рекомендованная литература

1. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 48-57.

2. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 30-34.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

План

1. Механические колебания. Уравнения малых колебаний.

2. Свободные гармонические колебания.

3. Пружинный осциллятор.

4. Физический маятник.

5. Математический маятник.

6. Затухающие колебания.

7. Вынужденные колебания.

8. Резонанс.

9. Автоколебания.

10. Примеры использования механических колебаний.

Мы живем в мире колебаний. Маятник стенных часов, фундамент быстроходной турбины, кузов железнодорожного вагона, струна гитары и т.д. совершают различные колебания.

По современным воззрениям, все звуковые, тепловые, световые, электрические и магнитные явления, то есть важнейшие физические процессы окружающего нас мира, сводятся к различным формам колебания материи. Колебания играют важную роль в таких ведущих областях техники, как электричество, радио, телекоммуникации. Выработка, передача и потребление электрической энергии, телефония, радиовещание, телевидение, радиолокация – все эти важные отрасли основаны на использовании электрических и электромагнитных колебаний. С колебаниями мы встречаемся и в живом организме. Биение сердца, сокращение желудка, деятельность кишечника имеют колебательный характер. Строители и механики имеют дело с колебаниями сооружений и машин. Кораблестроители – с качкой и вибрацией корабля и т.д.

Из истории науки. Уже в студенческие годы великий итальянский ученый Галилео Галилей (1564-1642) увлекался изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса. Сохранилось предание о том, как молодой студент медицинского факультета Г. Галилей в одно из воскресений 1583 года с интересом следил за качаниями зажженных лампад в церкви. По ударам пульса он определил время, необходимое для полного размаха лампад. С этого времени медицину пришлось ему оставить и сосредоточиться на физике.

Г. Галилей опубликовал исследование колебаний маятника и заявил, что период колебаний не зависит от их амплитуды (это приблизительно верно для малых амплитуд). Он также обнаружил, что периоды колебаний маятника соотносятся как квадратные корни из его длины. Результаты Г. Галилея привлекли внимание Х. Гюйгенса (1629-1695).

В 1673 году выходит в свет сочинение Х. Гюйгенса «Маятниковые часы». В этом сочинении ученый устанавливает, что свойством изохронности обладает циклоида, и разбирает математические свойства циклоиды.

В 1657 году Х. Гюйгенс издал описание устройства изобретённых им часов с маятником. В то время учёные не располагали таким необходимым для экспериментов прибором, как точные часы. Г. Галилей, например, при изучении законов падения считал удары собственного пульса. Часы с колесами, приводимыми в движение гирями, были в употреблении с давнего времени, но точность их была неудовлетворительна. Маятник же со времен Г. Галилея употребляли отдельно для точного измерения небольших промежутков времени, причём приходилось вести счёт числу качаний. Часы Х. Гюйгенса обладали хорошей точностью, и учёный далее неоднократно, на протяжении почти 40 лет, обращался к своему изобретению, совершенствуя его и изучая свойства маятника. Х. Гюйгенс намеревался применить маятниковые часы для решения задачи определения долготы на море, но существенного продвижения не добился. Надёжный и точный морской хронометр появился только в 1735 году в Великобритании.

В 1673 году в первой части труда «Маятниковые часы» Х. Гюйгенс описывает усовершенствованный, циклоидальный маятник, который обладает постоянным временем качания независимо от амплитуды. Для объяснения этого свойства автор посвящает вторую часть книги выводу общих законов движения тел в поле тяжести – свободных, движущихся по наклонной плоскости, скатывающихся по циклоиде. Это усовершенствование не нашло практического применения, поскольку при малых колебаниях повышение точности от циклоидального привеса незначительно. Однако сама методика исследования вошла в золотой фонд науки.

В четвёртой части Х. Гюйгенс изложил теорию физического маятника. Х. Гюйгенс решает ту задачу, которая не давалась стольким современным ему геометрам, – задачу об определении центра качаний. Он основывается на следующем предложении: «Если сложный маятник, выйдя из покоя, совершил некоторую часть своего качания, большую полуразмаха, и если связь между всеми его частицами будет уничтожена, то каждая из этих частиц поднимется на такую высоту, что общий центр тяжести их при этом будет на той высоте, на которой он был при выходе маятника из покоя».

Это предложение, не доказанное у Х. Гюйгенса, является у него в качестве основного начала, между тем как теперь оно представляет простое следствие закона сохранения энергии.

Теория физического маятника дана Х. Гюйгенсом в общем виде и в применении к телам разного рода. Х. Гюйгенс исправил ошибку Г. Галилея и показал, что провозглашённая последним изохронность колебаний маятника имеет место лишь приближённо.

1 Механические колебания. Уравнение малых колебаний

В общем случае колебаниями называют любые периодические движения, ограниченные в пространстве. Из всех возможных выделяют гармонические колебания, реализующиеся при малых амплитудах.

Пусть на тело, помещенное в вязкую среду (рис. 9.1), действуют постоянная во времени сила и упругая сила . В этом случае при малых колебаниях возникает сила вязкого трения:

Запишем II закон Ньютона для тела, массой m, помещенного в вязкую среду:

Последнее уравнение представляет собой дифференциальное уравнение малых колебаний. Каждое слагаемое этого уравнения делим на m:

где – коэффициент затухания,

– частота собственных колебаний.

С учетом коэффициента затухания и частоты собственных колебаний дифференциальное уравнение малых колебаний запишется в виде:

2 Свободные гармонические колебания

В случае отсутствия сопротивления среды, т.е. затухания (), уравнение малых колебаний принимает вид уравнения гармонических колебаний или уравнения гармонического осциллятора:

Осциллятор (от лат. – качаюсь) – система, совершающая колебания, то есть показатели которой периодически повторяются во времени. Понятие осциллятора играет важную роль в теории твёрдого тела, электромагнитных излучений, колебательных спектров молекул. Примеры простейших осцилляторов – маятник и колебательный контур.

Решение уравнения малых колебаний ищется в виде:

, ,

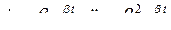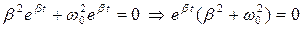Так как , то . Следовательно, , а .

Используя формулу Эйлера: , выделяем вещественную часть и получаем решение гармонических колебаний в виде:

где a₀ – амплитуда – наибольшее отклонение от положения равновесия; () – фаза колебаний – характеризует состояние системы в любой момент времени; φ₀ – начальная фаза – показывает состояние системы в начальный момент времени; ω₀ – циклическая частота колебаний – количество колебаний за 2π секунд, :

υ – частота колебаний – количество колебаний в единицу времени (за одну секунду), ;

Т – период колебаний – время одного колебания, :

3 Пружинный осциллятор

Собственная частота колебаний пружинного осциллятора (рис. 9.2) равна:

Тогда уравнение гармонических колебаний пружинного осциллятора принимает вид:

а его период колебаний определяется по формуле:

4 Физический маятник

Физический маятник представляет собой твердое тело, совершающее колебания относительно оси, не совпадающей с центром масс под действием силы тяжести.

Согласно основному уравнению динамики вращательного движения тела с закрепленной осью вращения момент силы тяжести сообщает телу угловое ускорение:

По определению момента силы момент силы тяжести равен:

где – плечо силы тяжести .

По определению углового ускорения:

Тогда основное уравнение динамики вращательного движения тела с закрепленной осью вращения можно переписать в виде:

Для малых колебаний (φ << 1рад) выполняется приближение: (рад). Поэтому можно записать:

Разделим последнее уравнение на J и сравним с уравнением гармонического осциллятора:

Из сравнения видно, что собственная частота колебаний физического маятника равна:

где – момент инерции маятника относительно оси вращения, a – расстояние от оси вращения до центра масс. Тогда период колебаний физического маятника равен:

5 Математический маятник

Математический маятник – физическая модель маятника, в которой материальная точка совершает колебания на длинной тонкой нерастяжимой нити.

Математический маятник – частный случай физического маятника. Для физического маятника период равен:

По теореме Штейнера:

где J_c – момент инерции материальной точки. Тогда период колебаний математического маятника:

Собственная частота колебаний математического маятника будет равна:

6 Затухающие колебания

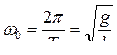Если к механической колебательной системе не подводится энергия, то при наличии сил трения механическая энергия преобразуется в тепло, и колебания затухают.

Дифференциальное уравнение затухающих колебаний имеет вид:

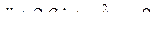при F(t)=0.

Решение этого уравнения ищется в виде:

При малых колебаниях β<<ω₀, поэтому

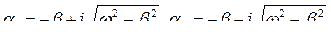Тогда общее решение уравнения затухающих колебаний имеет вид:

После выделения действительной части получаем частное решение уравнения затухающих колебаний:

где – закон изменения амплитуды затухающих колебаний (рис. 9.5).

Характеристикой затухающих колебаний является логарифмический декремент затухания, численно равный логарифму отношения двух последующих амплитуд:

Энергетической характеристикой затухания является добротность колебательной системы, которая характеризует относительные потери энергии в системе за один период:

где W – запасенная энергия,

ΔW – потери энергии за один период.

Добротность колебательной системы можно вычислять по формулам:

где N_e – количество колебаний системы за время релаксации.

Время релаксации – время, в течение которого амплитуда колебаний уменьшится в e раз.

7 Вынужденные колебания

Вынужденные колебания – это колебания, происходящие под действием внешней периодической силы.

Уравнение вынужденных колебаний:

Координата тела при вынужденных колебаниях отстает по фазе от внешней вынуждающей силы на величину j. Если сила изменится по закону:

то координата тела будет изменяться по закону:

Это связано с явлениями инерции и вязкости.

Амплитуда вынужденных колебаний и фазовый сдвиг j зависят от частоты колебаний.

Вынужденные колебания могут возникать в самых разнообразных условиях. Например, колебательное движение судна на море. Переменная сила плавучести, действующая на небольшой корабль, и неуравновешенная сила короткозамкнутого ротора (короткозамкнутая обмотка ротора, часто называемая «беличья клетка» из-за внешней схожести конструкции, состоит из медных или алюминиевых стержней, замкнутых накоротко с торцов ротора двумя кольцами) также вызывают колебания с частотой, равной частоте возбуждения. Поэтому следует особо выделять «качку». Дело в том, что вынуждающая сила вызывает при «качке» значительные перемещения, когда ее частота существенно ниже частоты свободных колебаний системы, которые сопровождаются деформациями.

Вибрации кормовой части судна вызываются гидродинамическими силами, которые возникают, когда лопасти гребного винта проходят вблизи обшивки корабля.

Совершенно иной источник возбуждения имеет место в ковшовой турбине. Такая турбина представляет собой хорошо сконструированное водяное колесо с ковшами определенной формы, расположенными по ее ободу; струя воды в направлении касательной к ободу турбины (обычно с очень большой скоростью) воздействует па турбину и приводит ее во вращение, причем каждый ковш испытывает периодические удары.

8 Резонанс

Если поддерживаются колебания с собственной частотой, то они оказываются особенно значительными. Если частота вынуждающей силы равна, или почти равна, собственной частоте системы, то следует ожидать интенсивных колебаний, связанных с резонансом (рис. 9.6).

Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынужденных колебаний к частоте собственных колебаний системы.

Отличие вынужденных колебаний от вынужденных резонансных колебаний определяется отношением частоты возбуждения к низшей собственной частоте системы. Собственную частоту вынужденных колебаний называют резонансной или характеристической.

Резонансная частота равна:

Если коэффициент затухания 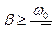, то резонанс невозможен и спектр колебаний является релаксационным.

Резонанс носит разрушительный характер. Резонансные колебания являются одной из причин поломки лопаток турбомашин, где в установившемся режиме движения каждая лопатка проходит какое-нибудь определенное положение через точно установленные промежутки времени. Если, например, лопасть гидротурбины получает повторяющиеся через определенные интервалы времени импульсы, то в результате резонанса лопасть может сломаться.

Разрушительный характер резонанса делает необходимыми исследования различных механических систем на резонанс, определяя собственную и резонансную частоту зданий, мостов, башен, самолетов. В некоторых реальных сооружениях рассеяние энергии весьма мало, например, в подвесных мостах. В этом случае совсем малая переменная сила может вызвать опасные резонансные колебания. Так, солдатский «шаг на месте» иногда применяется для возбуждения колебаний при испытании мостов новой конструкции; конечно, при этом необходима большая осторожность. Обычно даже небольшой отряд солдат, подходя к мосту, перестает маршировать и начинает идти не в ногу. Если ритм солдатских шагов совпадает с собственной частотой моста, то возможно даже его разрушение. Такой случай в действительности имел место в 1831 г. в Манчестере, когда 60 человек разрушили Браутонский подвесной мост через реку Ирвель. Аналогичный случай имел место в 1868 г., когда в Чатаме (Великобритания) рухнул мост на опорах при прохождении отряда британской морской пехоты. Но наиболее трагическая катастрофа произошла в 1850 г., когда в 300 км от Парижа был разрушен Анжерский подвесной мост батальоном французской пехоты численностью 500 человек. Разрушенный мост увлек людей за собой в ущелье, и погибло 226 человек. В 1906 году из-за резонанса разрушился и так называемый Егитпетский мост в Петербурге.

Позитивный характер явления резонанса используется ввибраторных системах.

9 Автоколебания

Огромный интерес представляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Поэтому используются автоколебания – незатухающие колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем свойства этих колебаний определяются самой системой.

Автоколебания принципиально отличаются от свободных незатухающих колебаний. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии определенными порциями в определенный момент времени (маятниковые часы). Энергия берется за счет раскручивающейся пружины либо за счет опускания груза.

Механические автоколебательные системы широко распространены в окружающей нас жизни и в технике. Колебания воздуха в духовых инструментах, органных трубах, струны смычковых музыкальных инструментов, голосовые связки при разговоре или пении и т.д. возникают вследствие автоколебаний, поддерживаемых воздушной струей. Автоколебания совершают паровые машины, двигатели внутреннего сгорания, электрические звонки и т.д. Примерами автоколебательных систем являются двигатель внутреннего сгорания, паровые турбины, ламповый или транзисторный генератор.

10 Примеры использования механических колебаний

Пример 1. Маятник Фуко – маятник, используемый для экспериментальной демонстрации суточного вращения Земли.

Впервые публичная демонстрация была осуществлена французским физиком и астрономом Леоном Фуко (1819-1868) в Парижском Пантеоне в 1851 г. Под куполом Пантеона он подвесил металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке длиной 67 м. Крепление маятника позволяло ему свободно колебаться во всех направлениях. Под точкой крепления было сделано круговое ограждение диаметром 6 метров, по краю ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём движении мог при её пересечении прочерчивать на песке отметки (рис. 9.7). Чтобы избежать бокового толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку пережгли.

Период колебания маятника при такой длине подвеса составлял 16,4 секунд, при каждом колебании отклонение от предыдущего пересечения песчаной дорожки составляло примерно 3 мм, за час плоскость колебаний маятника повернулась более чем на 11^о по часовой стрелке, то есть примерно за 32 часа совершила полный оборот и вернулась в прежнее положение.

Маятник Фуко является математическим маятником. Такой маятник, отклонённый от равновесного положения, совершает колебания в плоскости, неподвижной в инерциальной системе отсчёта «связанной» со звёздами, и проявляет, таким образом, свойства гироскопа.

Наблюдатель, находящийся на Земле и вращающийся вместе с нею, находится в неинерциальной (вращающейся) системе отсчёта и будет видеть, что плоскость колебаний маятника медленно поворачивается относительно земной поверхности в сторону, противоположную направлению вращения Земли.

На Северном или Южном полюсе ось вращения Земли лежит в плоскости колебаний маятника (рис. 9.8). Плоскость колебаний маятника Фуко совершает поворот на 360° за звёздные сутки (на 15° за звёздный час). На экваторе ось вращения Земли перпендикулярна плоскости колебаний маятника и плоскость колебаний маятника Фуко неподвижна. В произвольной точке с географической широтой φ угол между осью вращения Земли и плоскостью колебаний маятника равен: .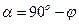

Скорость вращения плоскости колебаний идеального маятника Фуко Ω (в градусах в звёздный час) относительно поверхности Земли составляет

Для неидеального маятника Фуко скорость вращения плоскости колебаний зависит и от длины подвеса:

где а – амплитуда колебаний груза маятника; – длина нити. Поэтому для демонстраций применяют маятники с максимально возможной длиной подвеса.

В ночь с 11 на 12 апреля 1931 года в Ленинграде в Исаакиевском соборе был запущен маятник Фуко. Тогда это назвали триумфом науки над религией.

Однако представители церкви отметили, что этот опыт никак не опровергает догмат существования Бога. Хранитель экспозиции Исаакиевского собора Сергей Окунев прокомментировал это так: «На самом деле, всё было наоборот. Первый опыт Фуко был выполнен с благословения папы Римского для того, чтобы доказать могущество Бога».

Пример 2 – Часовой механизм с анкерным ходом. Примером механической автоколебательной системы может служить часовой механизм с анкерным ходом (рис. 9.9). Ходовое колесо с косыми зубьями жестко скреплено с зубчатым барабаном, через который перекинута цепочка с гирей. На верхнем конце маятника закреплен анкер (якорек) с двумя пластинками из твердого материала, изогнутыми по дуге окружности с центром на оси маятника. В ручных часах гиря заменяется пружиной, а маятник – балансиром – маховичком, скрепленным со спиральной пружиной.

Балансир совершает крутильные колебания вокруг своей оси. Колебательной системой в часах является маятник или балансир. Источником энергии – поднятая вверх гиря или заведенная пружина. Устройством, с помощью которого осуществляется обратная связь, является анкер, позволяющий ходовому колесу повернуться на один зубец за один полупериод.

Взаимодействием анкера с ходовым колесом осуществляется обратная связь. При каждом колебании маятника зубец ходового колеса толкает анкерную вилку в направлении движения маятника, передавая ему некоторую порцию энергии, которая компенсирует потери энергии на трение. Таким образом, потенциальная энергия гири (или закрученной пружины) постепенно, отдельными порциями передается маятнику.

Вопросы и задания для самоконтроля

1. Рассмотрите историю создания теории механических колебаний и составьте хронологическую таблицу ее развития.

2. Выведите дифференциальное уравнение малых колебаний. При каких условиях оно выполняется?

3. Что характеризует коэффициент затухания? В каких единицах измеряется коэффициент затухания?

4. Какие колебания называются свободными гармоническими?

5. Что в физике называется гармоническим осциллятором?

6. Получите уравнение гармонического осциллятора и его частное решение. Как называют частное решение уравнения гармонического осциллятора?

7. Какие характеристики гармонических колебаний Вы знаете? Что они характеризуют и как отражаются в уравнении гармонических колебаний?

8. Как определяются периоды и собственные частоты колебаний пружинного, физического и математического маятников?

9. Какие колебания называются затухающими?

10. Получите уравнение затухающих колебаний. Как зависит амплитуда затухающих колебаний от коэффициента затухания?

11. Раскройте физический смысл логарифмического декремента затухания и добротности колебательной системы.

12. Какие колебания называются вынужденными?

13. Получите уравнение затухающих колебаний и его частное решение.

14. Когда и при каких условиях мы встречаемся с явлением вынужденных колебаний? Какое явление называется резонансом?

15. Какие колебания называют автоколебаниями?

16. Один из элементарных способов решения занимательной задачи П.Л. Капицы об облачности Венеры является измерение длины суток при помощи маятника Фуко.

Текст задачи: «Астрономические наблюдения показывают, что на планете Венера полная облачность, так что «жители» Венеры лишены возможности наблюдать небесные светила. Опишите, каким методом они могли бы точно измерить длину своих суток».

17. В кабине аэростата установлены маятниковые часы. Аэростат начинает подниматься вверх с ускорением а без начальной скорости. Определите, на какую высоту h он поднимется за тот промежуток времени, когда по маятниковым часам пройдет промежуток времени t.

18. Для возбуждения колебаний груз массой m прикрепили к нижнему концу недеформированной пружины жесткостью k и отпустили. Затем к грузу в нижней точке траектории без толчка прикрепили груз такой же массой. Определите амплитуду A результирующих колебаний.

19. Математический маятник, представляющий собой железный шарик массой m, висящий на длинной нити, имеет период колебаний Т_o. Если ниже шарика расположить широкий магнит, то период колебаний шарика станет Т (Т < Т_o). Определите силу F, действующую на шарик со стороны магнита.

20. Маятник Галилея представляет собой математический маятник длиной L, совершающий колебания вблизи вертикальной стенки, в которую на расстоянии l под точкой подвеса вбит гвоздь. Определите период малых колебаний Т маятника Галилея.

21. Подставка совершает гармонические колебания в вертикальном направлении с амплитудой А = 0,30 м. Определите наименьший период колебаний T_min, при котором тело, лежащее на подставке, еще не будет отрываться от нее.

22. Автомобиль массой m при движении по неровной дороге совершает гармонические колебания в вертикальном направлении с периодом Т и амплитудой А. Определите максимальную силу давления F, действующую на каждую из четырех рессор автомобиля.

Рекомендованная литература

1. Волькенштейн В.С. Сборник задач по общему курсу физики. – М.: Главная ред. физ.-мат. литературы, 1987. – 456 с. – (Задачи №№ 12.1-12.54).

2. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М. Высшая школа, 1978. – 512 с. – С. 328-334.

3. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 157-160.

4. Трофимова Т.И. Курс физики. – М.: Высшая школы, 1990. – 478 с. – С. 219-232.

5. Шубин А.С. Курс общей физики: Учебн. пособие для инж. специальностей вузов. – Изд. 4-е. – М.: ВШ., 1996. – 480 с. – С. 50-66.

ВОЛНЫ

План

1. Характеристики волны.

2. Уравнение бегущей волны.

3. Волновое уравнение.

4. Принцип суперпозиции волн.

5. Интерференция волн.

6. Стоячие волны.

7. Звуковые волны.

8. Эффект Доплера.

9. Примеры проявления и использования волновых явлений.

Волна – изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве.

Волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины – например, плотности вещества, напряжённости электрического поля, температуры (рис. 10.1).

В связи с этим волновой процесс может иметь самую разную физическую природу: механическую, гравитационную (гравитационные волны), химическую (реакция Белоусова-Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO₃), электромагнитную (электромагнитное излучение), спиновую (магнон), плотности вероятности (ток вероятности) и т.д.

Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и она.

Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов. Об этих законах говорят как о волновых уравнениях – дифференциальных уравнениях в частных производных в фазовом пространстве системы. Для сред описание волновых процессов часто сводится к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.

По своему характеру волны подразделяют на:

v по признаку распространения в пространстве: стоячие, бегущие;

v по характеру волны: колебательные, уединённые (солитоны);

v по типу волн: поперечные, продольные, смешанного типа;

v по законам, описывающим волновой процесс: линейные, нелинейные;

v по свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях;

v по геометрии: сферические (пространственные), одномерные (плоские), спиральные.

Отличие колебания от волны. Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»).

В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков.

Создавая теорию света, Христиан Гюйгенс в 1690 г. систематизировал и обобщил основные понятия теории волн.

1 Характеристики волны

Волной или волновым процессом называется процесс распространения колебания в упругой среде. Вместе с волной от частицы к частице среды передается состояния колебательного движения и его энергия. Поэтому основным свойством всех волн являются перенос энергии без переноса вещества.

Рассмотрим типы волн (рис. 10.2).

Продольные – волны, у которых направление распространения волн совпадает с направлением колебаний частиц среды.

Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформациях сжатия и растяжения, т.е. в жидких, твердых и газообразных телах (рис. 10.2-1).

Поперечные волны – волны, у которых направление колебаний частиц среды перпендикулярно направлению распространения волны. Поперечные волны распространяются в средах, в которых возникает деформация сдвига, т.е. в твердых телах (рис. 10.2-2).

Упругие волны называются гармоническими, если их характеристики изменяются по гармоническому закону.

Волны характеризуются длиной, частотой и скоростью распространения.

Длина волны (λ) – расстояние между двумя точками волны, совершающими колебания в одинаковых фазах (рис. 10.3).

Частота волны (ν) – количество колебаний частиц упругой среды в единицу времени (в одну секунду).

Период волны (Т) – время, за которое волна проходит расстояние, равное длине волны.

В СИ: λ = [ м ], ν = [ Гц ], Т = [ с ].

Взаимосвязь между длиной, частотой и скоростью распространения волны:

Волновой фронт – геометрическое место точек, до которых дошло колебание к моменту времени t. Волновая поверхность – геометрическое место точек, колеблющихся в одинаковых фазах.

Если волновая поверхность представляет собой совокупность плоскостей, параллельных друг другу, то волна называется плоской, если концентрических сфер – сферическая (рис. 10.4).

Первый шаг в создании волновой теории был сделан Христианом Гюйгенсом. Он предположил, что каждый элемент поверхности, которой достигла в данный момент волна (т.е. каждая точка волнового фронта) является центром вторичных волн, огибающая которых в направлении движения волны становится волновым фронтом в более поздний момент времени (рис. 10.4). Этот принцип, который применим ко всем волновым явлениям в материальных средах, известен как принцип Гюйгенса.

2 Уравнение бегущей волны

Уравнение бегущей волны устанавливает зависимость смещения колеблющейся частицы от координат и времени:

Для получения уравнения бегущей волны на рис. 10.3 выберем точку (частицу среды), находящуюся на расстоянии Х от источника колебаний, которая совершает колебания, как и все точки волны в плоскости по закону:

но колебания частицы будут отставать от колебания источника по времени:

где V – скорость распространения волны.

Поэтому уравнение бегущей волны для частиц в плоскости будет иметь вид:

Если волна распространяется в другую сторону, то

В общем случае уравнение плоской волны записывается в виде:

Рассмотрим фазу этой волны:

, где – волновое число:

Тогда уравнение бегущей плоской волны будет иметь вид:

где – фазовая скорость.

Аналогично можно записать уравнение сферической волны:

где r – радиус волновой поверхности,

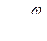– фазовая скорость сферической волны.

3 Волновое уравнение

Волновое уравнение описывает распространение волн и является дифференциальным уравнением в частных производных:

где выражение – оператор Лапласа, V – скорость распространения волн.

4 Принцип суперпозиции волн

Если свойства среды не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции ( наложения волн ).

При распространении волн в упругой линейной среде волны распространяются, не препятствуя распространению друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвующие в каждом волновом процессе (рис. 10.5).

Любая волна может быть представлена в виде геометрической суммы волн (в виде волнового пакета).

Волновой пакет – суперпозиция волн, мало отличающихся друг от друга по частоте и занимающих в любой момент времени ограниченную область пространства (рис. 10.6).

Для любого волнового пакета определяют групповую и фазовую скорость:

– групповая скорость;

– связь между групповой и фазовой скоростями.

Этот принцип имеет в физике большое значение. Принцип суперпозиции (наложения) – это допущение, согласно которому результирующий эффект представляет собой сумму эффектов, вызываемых каждым воздействующим явлением в отдельности. Одним из простых примеров является правило параллелограмма, в соответствии с которым складываются две силы, воздействующие на тело. Принцип суперпозиции выполняется лишь в условиях, когда воздействующие явления не влияют друг на друга. Встречный ветер тормозит движение автомашины по закону параллелограмма – принцип суперпозиции в этом случае выполняется полностью. Но если песок, поднятый ветром, ухудшит работу двигателя, то в этом случае принцип суперпозиции выполняться не будет. Вообще, в классической физике этот принцип не универсален и во многих случаях выполняется лишь приближенно.

В микромире, наоборот, принцип суперпозиции – фундаментальный принцип, который наряду с принципом неопределенности составляет основу математического аппарата квантовой механики. В квантовой теории принцип суперпозиции лишен наглядности, характерной для классической механики, так как в квантовой теории в суперпозиции складываются альтернативные, с классической точки зрения, исключающие друг друга состояния.

5 Интерференция волн

Волны называются когерентными, если они распространяются в упругой среде с одинаковой частотой и постоянной разностью фаз.

При наложении когерентных волн возникает усиление или ослабление результирующей волны. В этом заключается явление интерференции волн (рис. 10.7).

Пусть накладываются две волны:

и .

Амплитуда результирующей волны будет равна:

Для когерентных волн разность фаз остается постоянной:

Если , то наблюдается усиление волн (интерференционный максимум – светлые полосы на рис. 10.7).

Если , то наблюдается ослабление волн (интерференционный минимум – темные полосы на рис. 10.8).

6 Стоячие волны

Стоячие волны – волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами (рис. 10.9 и 10.10).

Пусть имеем две волны, распространяющиеся навстречу друг другу с одинаковыми частотами и амплитудами:

В результате наложения этих волн образуется результирующая волна:

Если , где , то амплитуда результирующей волны максимальна. Точки стоячей волны, в которых амплитуда максимальна, называются пучностями.

Если , где , то амплитуда минимальна. Точки стоячей волны, в которых амплитуда минимальна, называются узлами.

7 Звуковые волны

Акустика – это наука о звуке, название которой происходит от греческого слова (акуо) – «слышу». Оно было введено в науку в 1701 году французским ученым Ж. Совёром (1653-1716).

Из истории науки. Акустика – один из старейших разделов физики (ею занимались еще в Древнем Китае более чем за 3000 лет до н.э.). Больших успехов в исследовании явления звука достигли древние греки. Отдельного упоминания заслуживают создатели звуковых систем – Терпандр (VII век до н.э.), Пифагор Самосский (570-490 гг. до н.э.) и Дидим Александрийский (63 г. до н.э.-10 г. н.э.). Пифагор обнаружил связь между высотой тона и длиной струны или трубы. Аристотель (384-322 гг. до н.э.) понимал, что звучащее тело вызывает сжатия и разрежения воздуха, и объяснял эхо отражением звука от препятствий.

Период средневековья мало что дал развитию акустики. Её прогресс становится заметным, начиная с эпохи Возрождения. Леонардо да Винчи (1452-1519) исследовал отражение звука, сформулировал принцип независимости распространения звуковых волн от разных источников.

Период от начала XVII в. до начала XVIII в. характеризуется исследованиями системы музыкальных тонов, их источников (струны, трубы), скорости

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: