2020-05-12
347
Задача 1. Тело движется по горизонтальной плоскости под действием силы F, направленной под углом α к горизонту. Найти ускорение а тела, если на него действует сила F, а коэффициент трения между телом и плоскостью равен μ. При каком значении силы F движение будет равномерным?
Решение
1 Изобразив на чертеже к задаче (рис. 3.18) все силы, действующие на тело, записываем II закон Ньютона в векторном виде:
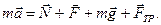
Выбираем оси координат OX и OY. Записываем II закон Ньютона в проекциях на выбранные оси (проекцией вектора на ось называется произведение модуля вектора на косинус угла между вектором и осью):
Из уравнения (2) определяем силу реакции опоры: 
По определению силы трения скольжения: 
Полученное значение силы трения подставляют в уравнение (1) и находят ускорение:
2 Определяем, при каком значении силы F движение будет равномерным. При равномерном движении ускорение равно нулю, следовательно, составляем уравнение равновесия в векторном виде: 
Записываем условие равновесия в проекциях на оси:
По определению силы трения скольжения: Полученное значение силы трения подставляем в уравнение (3) и находим значение силы F:
Задача 2. Определить ускорение а тела, соскальзывающего с наклонной плоскости, если угол наклона плоскости α = 30о, а коэффициент трения между телом и плоскостью равен μ = 0,3.
Решение
На чертеже изображаем все силы, действующие на тело (рис. 3.19) и записывают II закон Ньютона в векторном виде:
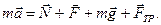
Выбираем оси координат OX и OY и записываем II закон Ньютона в проекциях на выбранные оси:
Из уравнения (2) определяем силу реакции опоры: 
По определению силы трения скольжения: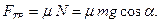 
Полученное значение силы трения подставляем в уравнение (1) и находим ускорение:
Задача 3. На горизонтальной плоскости находятся связанные невесомой и однородной нитью два тела, масса которых m1 и m2. К телу массой m2 приложена сила F, направленная под углом α к горизонту. Коэффициент трения между грузами и плоскостью равен μ. Определить натяжение нити T.
Решение
На чертеже изображаем все силы, действующие на тела системы (рис. 3.20) и записываем II закон Ньютона в векторном виде для всех тел системы:
Выбираем оси координат OX и OY и записываем II закон Ньютона в проекциях на выбранные оси:
Из уравнений (2) и (4) выражают силы реакции и определяют силы трения скольжения, действующие на оба тела:
Полученные формулы силы трения подставляем в уравнения (1) и (3):
Так как тела связаны однородной нерастяжимой нитью, то сила упругости, возникающая при деформации нити, во всех сечениях одинакова, следовательно:
Полученное значение ускорения подставляют в уравнение (5) или (6) и находят силу натяжения нити, связывающей тела:
Задача 4. Какой угол α с горизонтом составляет поверхность бензина в баке автомобиля, движущегося горизонтально с постоянным ускорением а = 2,44 м/с2?
Решение
Выполняют чертеж к решению задачи. Для этого выбирают элемент бензина на его поверхности и рассматривают силы, действующие на этот элемент: 
– сила реакции, 
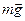– сила тяжести, 
– сила инерции, действующая со стороны автомобиля на бензин, численно равная произведению массы бензина на ускорение автомобиля и направленная в сторону, противоположную ускорению автомобиля (рис. 3.21).
Так как относительно автомобиля бензин сохраняет состояние покоя, то сумма сил, действующих на бензин равна нулю. Поэтому записываем І закон Ньютона в векторном виде
Выбираем оси координат OX и OY и записываем І закон Ньютона в проекциях на выбранные оси:
или: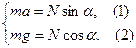 
Делим уравнение (1) на уравнение (2) и получаем: 
.
Окончательно:
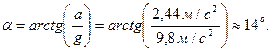
Вопросы и задания для самоконтроля
1. Рассмотрите историю развития понятий динамики и обоснуйте использование в научных исследованиях метода физического моделирования. Какие физические модели используются при решении задач на динамику?
2. Что изучает динамика? Охарактеризуйте основные понятия динамики.
3. Сформулируйте три закона Ньютона. Укажите условия. При которых они выполняются?
4. Определите силу тяжести. Как значение силы тяжести влияет на значение сил реакции и силы трения скольжения?
5. Сформулируйте определение веса тела. При каких условиях может наступить состояние невесомости?
6. Дайте определение массы, как меры инерции тела, и массы, как меры гравитационного взаимодействия.
7. Как связаны между собой законы Гука для различных видов деформаций?
8. При каких условиях возникает сила трения качения? Приведите примеры.
9. Обоснуйте исторический переход от скользящих механизмов к катящимся.
10. В чем заключается принцип относительности Г. Галилея?
11. Сформулируйте закон всемирного тяготения? Как определяется ускорение свободного падения на поверхности любой планеты?
12. Пользуясь таблицей 3.1 – «Некоторые данные о планетах Солнечной системы», определите ускорение свободного падения на Земле, Луне и любой планете Солнечной системы.
13. Пользуясь таблицей 3.1 – «Некоторые данные о планетах Солнечной системы», составьте и решите задачу на расчет силы всемирного тяготения.
Таблица 3.1 – Некоторые данные о планетах Солнечной системы
| Планета | Среднее расстояние от Солнца (млн. км) | Период обращения вокруг Солнца (зем. год) | Экваториальный диаметр (км) | Масса (кг) |
| Земля | 150 | 1 | 12742 | 5,96∙1024 |
| Луна | -- | -- | 1740 | 7,3∙1022 |
| Меркурий | 57,9 | 0,24 | 4840 | 3,22∙1023 |
| Венера | 108 | 0,62 | 12400 | 4,83∙1024 |
| Марс | 227,8 | 1,88 | 6780 | 6,38∙1023 |
| Юпитер | 777,8 | 11,86 | 139760 | 1,90∙1027 |
| Сатурн | 1426,1 | 29,46 | 115100 | 5,67∙1026 |
| Уран | 2869,1 | 84,02 | 51000 | 8,69∙1025 |
| Нептун | 4495,6 | 164,8 | 50000 | 1,03∙1026 |
| Плутон | 5229 | 249,7 | -- | -- |
10.
 |
Две гири массами 2 кг и 1 кг соединены нитью и перекинуты через невесомый неподвижный блок. Найти вес грузов во время движения. Трением нити о блок и весом нити пренебречь.
11. К одному концу верёвки, перекинутой через блок, подвешен груз массой 10 кг. С какой силой F нужно тянуть вниз за другой конец веревки, чтобы груз поднимался с ускорением 1 м/с2? Растяжением верёвки, её весом и трением о блок пренебречь (рис. 3.22).
12. Неподвижный блок подвешен к динамометру (рис. 3.23). Через блок перекинут невесомый шнур, на концах которого укреплены грузы с массами 2 кг и 8 кг. Что показывает динамометр при движении грузов? Весом блока и трением шнура пренебречь.
13. Задача про элементарный полиспаст. Найти натяжение нити Т в устройстве, изображенном на рисунке 3.24 к задаче. Массы тел равны 100 г и 300 г. Весом блоков и трением нити о них пренебречь. Определить ускорения тел.
Рекомендованная литература
1. Волькенштейн В.С. Сборник задач по общему курсу. – М.: Главная ред. физ.-мат. литературы, 1987. – 456 с. – (Задачи №№ 2.1-2.35).
2. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 57-67.
3. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 68-83.
4. Трофимова Т.И. Курс физики. – М.: ВШ, 1990. – 478 с. – С. 14-18.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. РЕАКТИВНОЕ ДВИЖЕНИЕ.
ЗАКОН ДВИЖЕНИЯ ЦЕНТРА МАСС
План
1 Механические системы.
2 Импульс.
3 Закон сохранения импульса.
4 Однородность пространства.
5 Центр масс.
6 Закон движения центра масс.
7 Уравнение движения тела переменной массы.
8 Формула Циолковского.
9 Примеры решения задач.
1 Механические системы
Механическими системами называют совокупность материальных точек тел, рассматриваемых как единое целое.
Механическими системами являются:
s материальная точка;
s математический маятник;
s абсолютно твердое тело;
s деформируемое тело;
S сплошная среда.
Тела (материальные точки) механической системы движутся согласно законам классической механики; взаимодействуют друг с другом и с телами, не включенными в эту совокупность.
Силы взаимодействия материальных точек механической системы между собой называют внутренними.
Внешними называют силы, с которыми на материальные точки механической системы действуют тела, в нее не входящие.
Механическая система является замкнутой (изолированной), если на нее не действуют внешние силы или действие внешних сил скомпенсировано. Для замкнутой системы по I закону Ньютона геометрическая сумма внутренних сил равна нулю.
2 Импульс
Понятие «количество движения» было введено И. Ньютоном в «Математических началах натуральной философии» (1687). Впоследствии это понятие было учеными заменено понятием «импульс». А в современной физике «количество движения» практически не используется.
Импульс – физическая величина, численно равная произведению массы тела на его скорость:
.
В СИ: 
.
3 Закон сохранения импульса
Рассмотрим механическую систему, состоящую из n тел, массы которых 
, а скорости – 
. Пусть 
– равнодействующие внутренних сил, действующие на тела системы, 
– равнодействующие внешних сил, действующих на каждое тело.
Запишем II закон Ньютона для каждого тела:
a 
a 
Просуммируем уравнения между собой:
;
Т.к. по ІІІ закону Ньютона 
, то:
.
Окончательно получаем II закон Ньютона для механической системы:
–
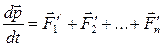первая производная от суммарного импульса замкнутой системы тел по времени равна геометрической сумме всех внешних сил, действующих на тела этой системы.
Для замкнутой механической системы сумма внешних сил, действующих на тела этой системы, равна нулю: 
. В этом случае 
, т.е.:
–
импульс замкнутой системы тел сохраняется, т.е. не изменяется со временем, при любых взаимодействиях между телами системы. Таким образом, из II закона Ньютона получен закон сохранения импульса.
При решении задач удобнее записывать закон сохранения импульса в форме:
,
в замкнутой механической системе геометрическая сумма импульсов тел до взаимодействия равна геометрической сумме импульсов тел после взаимодействия.
4 Однородность пространства
Однородность пространства заключается в том, что физические свойства механической системы и законы движения не зависят от выбора начала координат инерциальной системы отсчета.
Закон сохранения импульса является следствием однородности пространства.
5 Центр масс
Центр масс в механике – это геометрическая точка, характеризующая движение тела или системы частиц как целого.
Центр масс системы тел называется точка С, положение которой характеризует распределение масс в этой системе.
Радиус-вектор центра масс определяется выражением:
.
Понятие центра масс широко используется в физике.
Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.
Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.
Легко видеть, что в однородном поле тяготения центр масс совпадает с центром тяжести. Поэтому положение центра масс тела сложной формы можно практически определить путем последовательного подвешивания его за несколько точек и отмечая по отвесу вертикальные линии (рис. 4.2).
Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в состоянии безразличного равновесия. Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 4.2). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка.
6 Закон движения центра масс
Скорость центра масс равна первой производной радиус-вектора центра масс по времени:
.
Массу тела можно рассматривать как сумму элементарных масс системы:
.
Радиус-вектор центра масс определяется выражением:
.
Тогда скорость центра масс будет равна:
.
Следовательно,
–
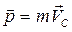импульс системы равен произведению массы механической системы на скорость центра масс.
Если полученное значение импульса системы подставить во II закон Ньютона для механической системы в дифференциальной форме, то получим:
,
–
закон движения центра масс: центр масс системы материальных точек движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему.
Вывод: для замкнутых систем действие внешних сил равно нулю или скомпенсировано:
, т.е. 
.
Следовательно, 
– т.е. центр масс замкнутых систем движется равномерно.
Центр масс замкнутой системы относительно произвольной инерциальной системы отсчета движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил.
Внутренние силы не влияют на характер движения замкнутой системы тел, если внешнее воздействие на систему постоянно и однородно. Например, во время салюта движение центра масс разорвавшегося пиротехнического снаряда в постоянном однородном поле силы тяжести происходит по параболе.
Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется. В качестве примера рассмотрим движение системы, состоящей из одного тела – снаряда. В случае падения одной из частей разорвавшегося в воздухе снаряда на землю в системе появится новая внешняя сила – сила реакции опоры. Характер движения центра масс системы (осколков снаряда) при этом изменится. Наличие внутренних сил в этом примере является необходимым условием изменения характера движения центра масс системы. Без этих сил, обусловивших распад снаряда на части, не произошло бы изменения траектории его движения вплоть до падения снаряда на землю.
7 Уравнение движения тела переменной массы
Пусть в момент времени t масса ракеты m, а скорость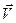 
. Через время dt масса ракеты изменилась на dm, а скорость ракеты на 
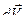. Тогда: 
– начальный импульс ракеты; 
– конечный импульс; 
– импульс вытекающих газов.
Найдем изменение импульса ракеты за время dt:
.
Если полученное выражение разделить на dt, то получим:
.
Если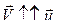 
, то ракета тормозится; если 
, то ракета движется с ускорением. Следовательно, 
– реактивная сила, которая создается вытекающими газами массы dm со скоростью 
.
Полученное уравнение:
носит название уравнения Мещерского – основное уравнение в механике тел переменной массы, полученное в 1904 году Иваном Всеволодовичем Мещерским (1859-1935), русским учёным, основоположником механики тел переменной массы. В выдающемся труде «Уравнения движения точки переменной массы в общем случае» (1904) его теория получила окончательное и в высшей степени изящное выражение. Здесь он устанавливает и исследует общее уравнение движения точки, масса которой изменяется от одновременного процесса присоединения и отделения материальных частиц.
И.В. Мещерский рассмотрел большое количество частных задач о движении точки переменной массы, например восходящее движение ракеты и вертикальное движение аэростата. Он подверг весьма обстоятельному исследованию движение точки переменной массы под действием центральной силы, заложив тем самым основания небесной механики тел переменной массы. Он исследовал также и некоторые проблемы движения комет.
И.В. Мещерский впервые сформулировал и так называемые обратные задачи, когда по заданным внешним силам и траекториям определяется закон изменения массы. Кроме работ по механике переменных масс, ему принадлежит ряд работ по общей механике.
С началом полётов в космос с достаточной полнотой выяснилось огромное практическое значение исследований И.В. Мещерского по механике переменных масс. Опираясь на его труды, учёные разработали основные вопросы динамики твёрдого тела произвольных изменяемых систем переменной массы.
Исследования И.В. Мещерского явились теоретической основой современной ракетодинамики. Его имя неразрывно связано с именем одного из создателей научных основ космонавтики – К.Э. Циолковского.
8 Формула Циолковского
Если система «ракета-газы» замкнута, то действие внешних сил отсутствует, т.е. 
. Тогда уравнение Мещерского преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:
при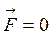 
, 
.
После интегрирования получим: 
.
В начальный момент времени, когда 
, 
, 
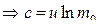. Тогда получаем:
–
формулу Циолковского, где определяется скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.
Формула Циолковского показывает, что:
1) чем больше конечная масса ракеты, тем больше стартовая масса ракеты;
2) чем больше скорость истечения газа, тем больше может быть конечная масса ракеты.
Из истории науки. Эта формула была выведена К.Э. Циолковским в рукописи «Ракета» 10 мая 1897 года. Однако первыми уравнение движения тела с переменной массой решили английские исследователи из Кембриджского университета У. Мур в 1810-1811 гг., а также П. Г. Тэйт и У. Дж. Стил в 1856 году.
Константин Эдуардович Циолковский (1857-1935) выдающийся исследователь, крупнейший ученый в области воздухоплавания, авиации и космонавтики, подлинный новатор в науке. Основное место в научном творчестве К.Э. Циолковского занимают вопросы ракетодинамики и космонавтики. Наиболее ранние записи К.Э. Циолковского по вопросам межпланетных сообщений относятся к 1878-1879 годам, когда он начал составлять «астрономические чертежи», тогда же им был сконструирован прибор для изучения действия на живой организм ускорения силы тяжести. Первой научной работой, в которой ученый высказал мысль о возможности использования принципа реактивного движения для перемещения в мировом пространстве, была монография «Свободное пространство» (1883г.).
В 1903 году в № 5 журнала «Научное обозрение» К.Э. Циолковский опубликовал работу «Исследование мировых пространств реактивными приборами». В ней впервые была научно обоснована возможность осуществления космических полетов при помощи жидкостных ракет и даны основные расчетные формулы их полета. Константин Эдуардович был первым в истории науки, кто строго сформулировал и исследовал прямолинейное движение ракет как тел переменной массы. В архиве Российской Академии наук сохранился листок, датированный 10 мая 1897 года, на котором была дана формула, устанавливающая зависимость между скоростью ракеты в любой момент времени, скоростью истечения газа из сопла двигателя, массой ракеты и массой израсходованных взрывчатых веществ.
Открытие К.Э. Циолковского указало основные пути совершенствования ракет: повышение скорости истечения газа и увеличения относительного запаса горючего. Вторая часть труда «Исследование мировых пространств реактивными приборами» была опубликована в 1911-1912 гг. в журнале «Вестник воздухоплавания». В 1914 году вышло дополнение к первой и второй части труда того же названия отдельной брошюрой в издании автора. Особенностью творческого метода ученого было единство научно-теоретического исследования и анализ и разработка возможных путей их практического осуществления. К.Э. Циолковский научно обосновал проблемы, связанные с ракетным космическим полетом. Детально рассмотрел все, что касается ракеты (одно- и многоступенчатой): законы движения ракеты, принцип ее конструкции, вопросы энергетики, управления, проведение испытаний, обеспечения надежности систем, создание приемлемых условий обитаемости и даже подбор психологически совместимого экипажа. Циолковский не ограничился тем, что указал на средство проникновения человека в космос – ракету, но и дал подробное описание двигателя. Пророческими оказались его идеи о выборе жидкого двухкомпонентного топлива, о регенеративном охлаждении камеры сгорания и сопла двигателя компонентами топлива, керамической изоляции элементов конструкции, раздельном хранении и насосной подаче компонентов топлива в камеру сгорания, об управлении вектором тяги путем поворота выходной части сопла и газовыми рулями. Думал ученый и о возможности использования других видов топлива, в частности, энергии распада атомов. Мысль об этом он высказал в 1911 году. В том же году К.Э. Циолковский выдвинул идею создания электрореактивных двигателей, указав, что «может быть с помощью электричества можно будет со временем придавать громадную скорость выбрасываемым из реактивного прибора частицам».
Ученый рассмотрел многие конкретные вопросы, касающиеся устройства космического корабля. В 1926 году К.Э. Циолковский для достижения первой космической скорости предложил применить двухступенчатую ракету. В 1929 году в работе «Космические ракетные поезда» дал стройную математическую теорию многоступенчатой ракеты; в 1934-1935 гг. в рукописи «Основы построения газовых машин, моторов и летательных аппаратов» предложил еще один способ достижения космических скоростей, получивший название «эскадры ракет».
Особенно большое значение придавал ученый проблеме создания межпланетных станций. В решении этой задачи он видел возможность осуществления давней мечты о завоевании человеком околосолнечного пространства, создания в будущем «эфирных поселений». К.Э. Циолковский наметил грандиозный план завоевания мировых пространств, который в настоящее время успешно осуществляется.
9 Примеры решения задач
Задача1. Шарик массой m = 100 г, движущийся со скоростью V = 1 м/с, упруго ударяется о вертикальную плоскость. Определить изменение импульса ΔP шарика, если направление вектора скорости составляет с плоскостью угол α, равный: 1) 90о, 2) 60о, 3) 30о.
Решение
Выполняем чертеж к задаче (рис. 4.3). При упругом столкновении: 1) модуль скорости после удара не изменяется, 2) угол падения равен углу отражения.
Раскладываем векторы скорости 
и 
на составляющие, параллельные осям OX и OY. Вертикальная составляющая вектора скорости не поменяла своего направления, т.е. 
. Поменяла направление горизонтальная составляющая скорости. Следовательно, изменение импульса происходит только относительно оси OX, а вклад в изменение импульса вносит горизонтальная составляющая скорости:
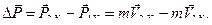
Записываем это уравнение в проекции на ось OX и рассчитываем изменение импульса:
Если α = 90о, то ΔP = 2·0,1 кг ·1 м/с · sin 90о = 0,2 кг·м/с.
Если α = 60о, то ΔP = 2·0,1 кг ·1 м/с · sin 60о = 0,173 кг·м/с.
Если α = 30о, то ΔP = 2·0,1 кг ·1 м/с · sin 30о = 0,1 кг·м/с.
Задача 2. На спокойной воде пруда перпендикулярно берегу и носом к нему стоит лодка массой М и длиной L. На корме стоит человек массой m. На какое расстояние S удалится лодка от берега, если человек перейдёт с кормы на нос лодки?
Решение
 |
Систему «человек-лодка» относительно горизонтального направления можно рассматривать как замкнутую (рис. 4.4). Согласно следствию из закона сохранения импульса, внутренние силы замкнутой системы тел не могут изменить положение центра масс системы. Применяя это следствие к системе «человек-лодка», можно считать, что при перемещении человека по лодке центр масс системы не изменит своего положения, т.е. останется на прежнем расстоянии от берега.
Пусть центр масс системы «человек-лодка» находится на вертикали, проходящей, в начальный момент через точку С1 лодки, а после перемещения лодки – через другую точку С2. Так как эта вертикаль неподвижна относительно берега, то искомое перемещение S лодки относительно берега равно перемещению лодки относительно вертикали. А это перемещение легко определить по перемещению центра масс лодки. Как видно из рисунка, в начальный момент точка O находится на расстоянии a1, слева от вертикали, а после перехода человека – на расстоянии a2 справа от вертикали. Следовательно, искомое перемещение лодки равно:
(1)
Для определения a1 и a2 воспользуемся тем, что результирующий момент сил, действующих на систему относительно горизонтальной оси, перпендикулярной продольной оси лодки, равен нулю. Потому для начального положения системы правило моментов записывают в виде:
. (2)
После перемещения лодки: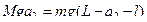 
,
(3)
Подставив выражения (2) и (3) в (1), получим:
.
Задача 3. Ледокол массой m = 6000 т, идущий с выключенным двигателем со скоростью V1 = 8 м/с, наталкивается на неподвижную льдину и движет её впереди себя. Скорость ледокола уменьшилась при этом до V2 = 3 м/с. Определить массу М льдины. Определить количество теплоты Q, выделившееся при столкновении льдины и ледокола.
Решение
Согласно закону сохранения импульса импульс замкнутой системы тел не изменяется при любых взаимодействиях между телами данной системы. В условии данной задачи рассматривается неупругое взаимодействие. Поэтому: 
Следовательно: 
Количество теплоты, выделившееся при столкновении льдины и ледокола равно изменению кинетической энергии системы «ледокол-льдина» до и после столкновения:
.
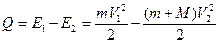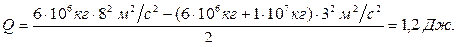
Вопросы и задания для самоконтроля
1. Какие системы называются механическими? Приведите примеры механических систем.
2. При каких условиях выполняется замкнутость механической системы?
3. Какая физическая величина называется импульсом? Назовите единицы измерения импульса.
4. Сформулируйте закон сохранения импульса. Как этот закон можно вывести из II закона Ньютона?
5. Какое свойство пространства приводит к закону сохранения импульса?
6. Какую роль в физических исследованиях и при решении задач играет роль понятие «центра масс» и «радиус-вектора центра масс»?
7. Какой физический смысл несет закон движения центра масс?
8. Выведите уравнение движения тела переменной массы. Приведите примеры, когда ученым можно использовать это уравнение в практической деятельности.
9. Рассмотрите историю жизнедеятельности и научного творчества И.В. Мещерского. Каково Ваше отношение к его деятельности?
10. Какую роль сыграла формула Циолковского в развитии космонавтики?
11. Рассмотрите историю жизнедеятельности и научного творчества К.Э. Циолковского. Обоснуйте Ваше отношение к его деятельности.
12. Работы каких украинских ученых и инженеров внесли свой вклад в развитие ракетостроения и космонавтики?
Рекомендованная литература
1. Волькенштейн В.С. Сборник задач по общему курсу физики. – М.: Главная ред. физ.-мат. литературы, 1987. – (Задачи №№ 2.61-2.72).
2. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 67-72.
3. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М.: Просвещение, 1982. – 448 с. – С. 430-433.
4. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1990. – 478 с. – С. 18-21.
РАБОТА, МОЩНОСТЬ, ЭНЕРГИЯ.
ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
План
1. Механическая работа.
2. Мощность.
3. Энергия.
4. Кинетическая энергия.
5. Потенциальные и непотенциальные силы.
6. Потенциальная энергия тела в однородном поле тяжести.
7. Центральные силы.
8. Потенциальная энергия гравитационного взаимодействия.
9. Потенциальная энергия упругой деформации.
10. Полная механическая энергия.
11. Закон сохранения полной механической энергии.
12. Примеры решения задач.
1 Механическая работа
Механической работой называется скалярное произведение силы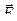 
на вектор элементарного перемещения 
:
.
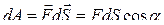Полная работа определяется интегралом:
.
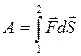В системе интернациональной работа измеряется в Джоулях: 
.
Из истории науки. Понятие о механической работе как произведении силы на путь, пройденный точкой ее приложения, установлено окончательно в 1826 году Г.Г. Кориолисом (1792-1843) и Ж. Понселе (1799-1867), который ввел и понятие о «килограммометре», как единице работы.
Однако уже Г. Галилей (1564-1642), Р. Декарт (1596-1650) и Г. Лейбниц (1646-1716) пользовались принципом механической работы под разными наименованиями: «измерение» механической работы, «измерение» энергии. Из этого можно заключить, что эти понятия подобны. И действительно, когда «измерение» силы, тратясь, преобразовывается в другой вид энергии, количество потраченной работы оказывается пропорциональным количеству произведенного вида энергии.
2 Мощность
Мощность – физическая величина, характеризующая работу, совершенную в единицу времени, т.е. скорость совершения работы, и численно равна первой производной от работы по времени:
.
В Системе интернациональной мощность измеряется в Ваттах:
.
Из истории науки. Пока не была изобретена паровая машина и все работы производились силами человека и животных, необходимости в измерении мощности. Естественно, отсутствовала тогда и соответствующая единица измерения.
Первые паровые машины применили в Англии для того, чтобы выкачивать воду из угольных шахт. Использование лошадей при выкачивании воды было дорогим, и потому, естественно, возник вопрос, сколько же лошадей может заменить одна машина.
Джеймс Уатт (1736-1819) использовал единицу мощности – «лошадиную силу» (1 л.с.), которую он ввел с целью возможности сравнения работоспособности паровой машины и лошади. Он опытным путем установил, что одна лошадь за 1 секунду на высоту в 1 фут груз массой в 550 фунтов. Сравнивая эти данные с аналогичными показателями машины, можно определить, скольких лошадей заменяют машины.
Так как один фунт равен приблизительно 0,454 кг и один фут составляет 0,305 м, то можно найти величину одной лошадиной силы (1 л.с.):
1 л.с. = (550∙0,454 кг ∙9,84 Н/кг ∙0,305 м)/1 с = 746 Вт.
Такая величина лошадиной силы применяется в Англии и Америке. У нас за лошадиную силу принимается мощность 1л.с. = 735,5 В т ≈ 736 Вт.
Лошадиную силу применяют для характеристики автомобильных и тракторных моторов.
Используя определение работы можно показать, что мощность численно равна скалярному произведению вектора силы на вектор скорости:
.
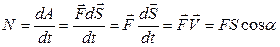Таким образом, мощность можно расходовать на тяговые усилия (трактор, бульдозер, асфальтовый каток и т.д.), а можно расходовать на увеличение скорости (гоночные машины и т.д.).
3 Энергия
Энергия – физическая величина, являющаяся общей количественной мерой всех форм движения и взаимодействия тел.
В системе интернациональной энергия измеряется в Джоулях:
[ E ] = [ W ] = [ Дж ] = [ Н·м ].
Из истории науки. Термин «энергия» происходит от слова energeia, которое впервые появилось в работах Аристотеля. Понятие «энергия» введено Г.В. Лейбницем (1646-1716), но сам термин появился позже.
Томас Юнг (1773-1829) первым использовал понятие «энергия» в современном смысле слова.
Маркиза Эмили дю Шатле в книге «Уроки физики» (фр. «Institutions de Physique»), опубликованной в 1740 году, объединила идею Г.В. Лейбница с практическими наблюдениями Виллема Гравесена (Willem Jacob 's Gravesande), чтобы показать: энергия движущегося объекта пропорциональна его массе и квадрату его скорости (не скорости самой по себе как полагал Ньютон).
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия «живая сила». Гюстав Гаспар Кориолиис (1792-1843) впервые использовал термин «кинетическая энергия» в 1829 году, а в 1853 году Уильям Ренкин (1820-1872) впервые ввёл понятие «потенциальная энергия».
4 Кинетическая энергия
Согласно ІІ закона Ньютона 
, где 
. Тогда:
.
Скалярное произведение 
равно произведению модулей 
. А так как при поступательном движении векторы 
и 
сонаправлены (рис. 5.2), то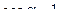 
. Следовательно: 
.
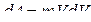После интегрирования этого выражения в пределах от 
до 
получим:
.
Физическую величину, численно равную половине произведения массы тела на квадрат его скорости, называют кинетической энергией.
Кинетическая энергия 
характеризуетэнергию движения.
Теорема об изменении кинетической энергии: работа по изменению скорости тела численно равна изменению кинетической энергии тела:
.
5 Потенциальные и непотенциальные силы
Все виды сил в природе делят на консервативные (потенциальные) и неконсервативные (непотенциальные).
Консервативные силы – это силы, работа которых не зависит от пути, а определяется начальным и конечным положением тела.
Неконсервативные силы – это силы, работа которых либо существенно зависит от пути либо равна нулю. Примером непотенциальных (неконсервативных) сил являются все виды сил трения. Определим работу силы трения (рис. 5.3):
.
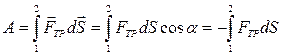Еще одним примером неконсервативных сил является сила Лоренца (сила, действующая со стороны магнитного поля на движущийся в нем заряд). Работа силы Лоренца равна нулю, т.к. сила Лоренца перпендикулярна скорости и перемещению заряда.
6 Потенциальная энергия тела в однородном поле силы тяжести
Однородность поля силы тяжести означает, что сила тяжести одинакова во всех точках пространства.
Рассмотрим работу силы тяжести по перемещению тела из точки 1 в точку 2 (рис. 5.4). Для этого траекторию движения разобьем на элементарные горизонтальные и вертикальные перемещения 
относительно оси OX и OY.
Горизонтальное смещение тела вклада в работу не дает: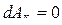 
. Вклад в работу дает только вертикальное перемещение тела (рис. 5.5): 
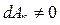. Тогда полная работа будет складываться из элементарных работ, производимых вдоль вертикального направления:
.
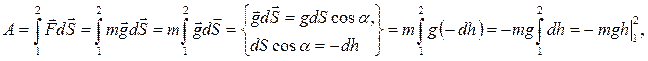
Величину, численно равную произведению массы тела на ускорение свободного падения и на высоту относительно нулевого уровня, называют потенциальной энергией тела: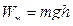 
.
Работа силы тяжести по изменению высоты тела относительно нулевого уровня численно равна изменению потенциальной энергии тела:
.
Так как работа силы тяжести зависит только от начального и конечного положения тела, то сила тяжести является консервативной.
7 Центральные силы
Центральные силы – это силы, аналитические выражения которых можно представить в виде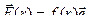 
, где f(r) – функция, зависящая от расстояния до силового центра (центр масс, заряд), 
– единичный вектор, направленный параллельно радиус-вектору.
Для центральных сил работа равна изменению потенциальной энергии 
и не зависит от пути, а зависит от начального и конечного положения тела. Следовательно, к центральным силам относятся силы всемирного тяготения, силы электростатического взаимодействия.
8 Потенциальная энергия гравитационного взаимодействия
Рассмотрим движение одного тела в поле тяготения другого (например, движение спутника в поле тяготения Земли – рис. 5.6).
 |
Сила тяготения, действующая на тело m2 со стороны поля тела массой m1, направлена по линии, соединяющей центры этих тел (т.е. удовлетворяет уравнению 
), равна:
.
Траекторию движения разобьем на участки, параллельные и перпендикулярные радиус-вектору. На участках, нормальных к радиус-вектору, работа по перемещению равна нулю 
т.к 
. Тогда полная работа по перемещению тела массой m2 из точки 1 в точку 2 будет равна:
,
где 
.
Тогда получим:
.
Величину, прямо пропорциональную произведению масс тел и обратно пропорциональную расстоянию между их центрами 
называют потенциальной энергией гравитационного взаимодействия.
Полная работа в поле тяготения равна изменению потенциальной энергии гравитационного взаимодействия 
. Полная работа в поле тяготения не зависит от пути, а зависит от начального и конечного положения тела. Следовательно, гравитационная сила является потенциальной.
9 Потенциальная энергия упругой деформации
Аналогично можно показать, что упругие силы также являются потенциальными. Их работа не зависит от пути, а равна изменению энергии упругодеформированного тела.
Величину, равную половине произведения коэффициента упругости на квадрат абсолютного удлинения 
называют потенциальной энергией упругой деформации.
Полная работа по растяжению (сжатию) упругого тела равна изменению потенциальной энергии упругой деформации:
или 
.
10 Полная механическая энергия
Полной механической энергией системы называют сумму кинетических энергий движения всех тел системы и потенциальной энергии взаимодействия тел между собой и внешними телами:
.
11 Закон сохранения полной механической энергии
Пусть механическая система состоит из n тел массами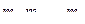 
, движущимися со скоростями 
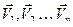. На эти тела действуют Fi – внешние консервативные силы, 
– внешние и внутренние неконсервативные силы, Fik – внутренние консервативные силы взаимодействия тел системы между собой (i ≠ k). Запишем II закон Ньютона для каждого тела механической системы:
Суммируем все слагаемые системы:
.
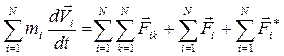Т.к. 
, то левую часть равенства умножим на 
, а каждое слагаемое правой части умножим на 
:
.
Рассмотрим каждое слагаемое полученного уравнения и получим:
– полный дифференциал кинетической энергии всех тел системы;
– полный дифференциал работы внешних консервативных сил;
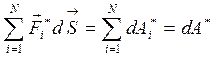– полный дифференциал работы неконсервативных сил;
– работа внутренних консервативных сил взаимодействия равна изменению потенциальной энергии взаимодействия.
Окончательно получаем:
То есть дифференциал полной механической энергии равен сумме дифференциалов работы неконсервативных и внешних консервативных сил:
.
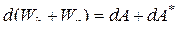Это выражение носит название закона изменения полной энергии.
Для замкнутой механической системы выполняется закон сохранения полной механической энергии в случае отсутствия неконсервативных сил:
–
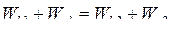в случае отсутствия неконсервативных сил полная механическая энергия остается неизменной.
В случае действия внутренних или внешних неконсервативных сил механическая энергия переходит в немеханические виды. Процесс перехода механической энергии в немеханические виды называется диссипацией энергии. Все механические системы являются диссипативными.
Из истории науки. В 1918 было доказано, что закон сохранения энергии есть математическое следствие трансляционной симметрии времени, величины сопряженной энергии. То есть энергия сохраняется, потому что законы физики не отличают разные моменты времени (Теорема Нётер об изотропии пространства).
В 1961 году выдающийся преподаватель физики и нобелевский лауреат, Ричард Фейнман в лекциях так выразился о концепции энергии: «Существует факт, или, если угодно, закон, управляющей всеми явлениями природы, всем, что было известно до сих пор. Исключений из этого закона не существует; насколько мы знаем, он абсолютно точен. Название его – сохранение энергии. Он утверждает, что существует определенная величина, называемая энергией, которая не меняется ни при каких превращениях, происходящих в природе. Само это утверждение весьма и весьма отвлечено. Это по существу математический принцип, утверждающий, что существует некоторая численная величина, которая не изменяется ни при каких обстоятельствах. Это отнюдь не описание механизма явления или чего-то конкретного, просто-напросто отмечается то странное обстоятельство, что можно подсчитать какое-то число и затем спокойно следить, как природа будет выкидывать любые свои трюки, а потом опять подсчитать это число – и оно останется прежним».
12 Примеры решения задач
Задача 1. Шар массой m1 движется со скоростью V1 и сталкивается с шаром массой m2, движущегося в том же направлении со скоростью V2. Определить скорости шаров после абсолютно упругого, прямого, центрального удара.
Из истории науки. На протяжении XVII в. физики решали проблему удара: что случается при столкновении тел и как оценивать эффект удара? С одной стороны проблема удара имела технический аспект (обработка металлов ударом, забивание молотком пали, действие пушечного ядра и т.д.), а с другой стороны проблема имела теоретическое значение. Ее решение касалось формированию основ динамики.
Частично задачу об ударе рассматривал Г. Галилей. Более подробно ее исследовал и решал французский естествоиспытатель и философ Рене Декарт (1596-1650). В 1639 г. была опубликована работа чешского ученого Йоханеса Марци (1595-1667) «О соотношении движений или правила столкновений». В работе «О соотношении движений или правила столкновений» Й. Марци рассмотрел три типа механических ударов (жесткие, мягкие, упругие). Он установил два правила: при столкновении движущегося тела с одинаковым весом и материалом оно останавливается, при столкновении двух одинаковых тел с одинаковыми, но противоположно направленными скоростями, они разлетаются после удара с одинаковыми, но противоположно направленными скоростями.
В 1668-1669 гг. Лондонское королевское общество объявило конкурс на лучшее исследование по теории столкновения тел. На конкурс представили свои работы английские ученые К. Рен (1632-1723), Дж. Валлис (1616-1703) и голландский ученый Х. Гюйгенс (1629-1695).
В конкурсной работе К. Рен изложил правила расчетов столкновений упругих тел, но не привел математического доказательства.
Джон Уоллис Валлис – математик – в конкурсной работе изложил основные законы неупругих столкновений, но тоже без доказательств. Доказательства он изложил позже в трактате «Механика или о движении» (1671), где получил формулу, которая является частным случаем закона сохранения импульса для неупругих столкновений.
Конкурсная работа Х. Гюйгенса по столкновению «твердых» тел была более подробной, но Лондонское общество ее опубликовало. Х. Гюйгенс в своей работе уже использовал законы сохранения энергии и количества движения.
Позже теоретически и практически задачу о столкновении тел решил французский ученый Е. Мариотт (1620-1684) – известен нам как один из авторов закона Бойля-Мариотта для изотермического газового процесса. В работе «О столкновения или об ударе тел» (1677) он описал экспериментальные методы исследования сталкивающихся тел.
Но подробное теоретическое исследование столкновения тел еще было невозможным, потому что не были сформулированы физические модели «абсолютно упругого» и «абсолютно неупругого» ударов, не были уточнены законы сохранения.
Только в 1727 г. Иоганн Бернулли (1667-1748) в мемуарах «Рассуждение о законах передачи движения» изложил теорию столкновения абсолютно упругих столкновений опиралась на три основных физических закона: 1) при абсолютно упругих столкновениях относительная скорость тел до и после столкновения не меняется; 2) закон сохранения количества движения (импульса); 3) «закон сохранения живых сил» – закон сохранения энергии. Опираясь на эти
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
|
|
