2020-05-12
86
Заменим сходящиеся силы в точках A и B их равнодействующими (рисунок 4.4):
Так как
= и P 2
P 1 + P 2 = R;
P 1¢+ P 2¢ = R ¢.
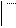
= P 2¢ , то
R = R ¢ .
M 1 (P 1, P 1¢)= AB ´ P 1 ;
M 2 (P 2 , P 2¢)= AB ´ P 2 .
Две пары (P 1, P 1¢) и
Рисунок 4.4
При сложении нескольких пар получим:
M = å Mi .
(P 2 , P 2¢), лежащие в пере- секающихся плоскостях,
можно заменить одной эк- вивалентной парой (R, R ¢),
момент которой равен геометрической сумме мо- ментов слагаемых сил:
M = M 1 + M 2;
 | |
M = AB ´ P 1 + AB ´ P 2 .
 | |
Если тело под действием системы пар находится в равновесии, то момент результирующей пары равняется нулю:
M = å Mi = 0.
В проекции на оси координат получим:
|
|
ïîå Miz = 0.
Если пары расположены в одной плоскости, векторы моментов их будут параллельны. Момент результирующей пары определится как алгебраическая сумма моментов пар:
M = å Mi .
ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ (ТОЧКЕ)
Теорема Пуансо о параллельном переносе силы
Не изменяя кинематического состояния твердого тела, силу, приложенную к нему в какой-либо точке, можно переносить параллельно ей самой в любую другую точку тела, прибавляя при этом пару с моментом M, равным моменту переносимой силы относительно точки, в которую переносится сила.
Пусть в точке A приложена сила P (рисунок 5.1). В произвольную точку O приложим уравновешенные силы P ¢ и
P ¢¢ , причем P
= P ¢ = P ¢
и линии
Рисунок 5.1
действия сил параллельны. Тогда получим силу P ¢ и пару сил (P, P ¢¢),
момент которой равен моменту силы P относительно точки O:
MO (P)= r ´ P; MO (P)= OA ´ P; MO (P)= Ph.
