Нахождение производной называется дифференцированием функции

Лекция на тему «Производная элементарных функций»

1. Понятие производной

Пусть  – некоторая функция, определенная на промежутке (a; b) и  - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x - . Разность x -  называют приращением независимой переменной (или приращением аргумента) функции  в точке  и обозначают :

= x - (1)

Приращением функции  в точке  называют разность между значением функции в точке и значением функции в точке  и обозначают :

=    (2).

Т.к. точка  считается фиксированной, приращением функции  является функцией приращения аргумента .

Составим отношение

,

которое также будет функцией приращения аргумента ; и рассмотрим предел этого выражения при , стремящемся к нулю:

 

                                                    .                 

Если этот предел существует, то говорят, что функция  имеет производную в точке , и пишут:

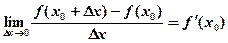(3).

Число  называется производной функции в точке .

Нахождение производной называется дифференцированием функции.

Если существует предел (3), также говорят, что функция   дифференцируема в точке .

Если функция  дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).

Производная функции , дифференцируемой в промежутке (a; b), сама является функцией x.

 

2. Правило нахождения производной

Чтобы вычислить производную функции в точке  нужно:

1. найти разность .

2. найти отношение .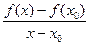

3. найти предел этого отношения при :

Производная – это «новая» функция, произведенная от данной функции по указанному правилу.

Определим производные следующих функций:

а) линейной функции

б) квадратичной функции

в) кубической функции

 

Решение:

а)          

  т.к.

1.

2.

3. .

б)

 

т.к.

1.

2.

3. .

 

в)

    

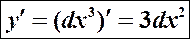
т.к.

1.

2.

3.

3. Правила и формулы дифференцирования

 

Правила и формулы дифференцирования следует обязательно знать, чтобы не повторять каждый раз все выкладки при нахождении данной функции. Ведь существует бесконечное множество функций и с их усложнением непосредственное дифференцирование становится все более трудоемким.

Поэтому целесообразно вывести формулы производных для основных элементарных функций (степенной, показательной, логарифмической, тригонометрической и обратной тригонометрической функций).