Обратные матрицы. Элементарные преобразования

Квадратная матрица порядка n

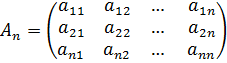 называется невырожденной, если её определитель (детерминант)

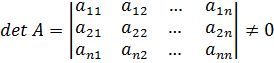
В случае, когда det A=0, матрица А называется вырожденной.

Матрица 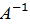 называется обратной для квадратной невырожденной матрицы А, если 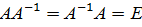, где Е-единая матрица порядка n:

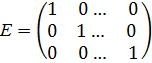
Известно, что для невырожденной матрицы А существует единственная обратная матрица 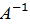, которая определяется формулой

 

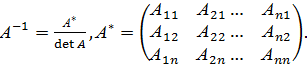
Матрица 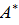 называется присоединенной, состоит из алгебраических дополнений  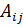элементов  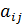матрицы А, записанных в транспонированном виде (строки замены столбцами с теми же номерами).

 

 

Пример:

Дана матрица А. Убедиться, что она невырожденная, найти обратную ей матрицу 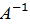 и проверить выполняемость равенств .

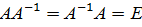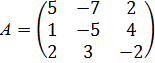
Решение:

 

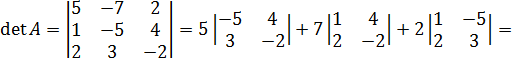
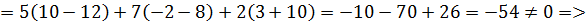
матрица А невырожденная.

Далее находим алгебраическое дополнение элементов матрицы А.

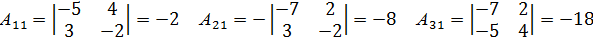
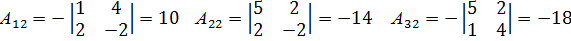
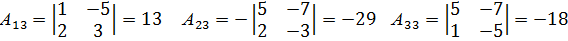
Обратная матрица:

 

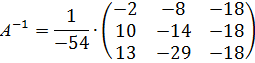
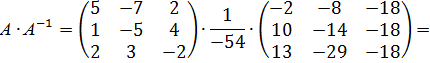
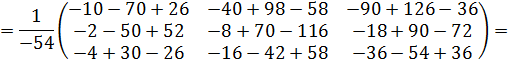
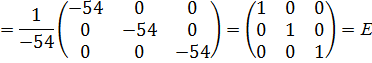
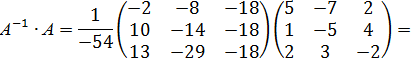
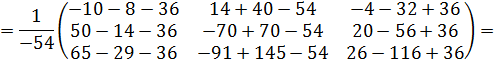
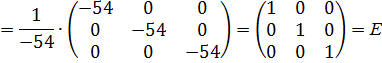
Элементарными называются следующие преобразования матриц:

1. Поменять местами любые 2 параллельных ряда матрицы;

2. Умножить каждый элемент ряда на один и тот же множитель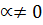

3. Прибавить у элементам ряда матрицы соответствующие элементы любого другого параллельного ряда. Ряд-это строка или столбец матрицы.

4. Определитель с двумя одинаковыми параллельными рядами равен нулю;

5. Если все элементы некоторого ряда определителя имеют общий множитель, то последний можно вынести за знак определителя;

6. Если все элементы какого-либо ряда определителя равны нулю, то определитель также равен нулю;

7. Определитель, у которого элементы двух параллельных рядов соответственно пропорциональны, равен нулю;

8. Определитель не изменится, если ко всем элементам какого-либо ряда прибавить соответствующие элементы другого параллельного ряда, умноженные на одно и то же произвольное число d.

 

Методы решения систем линейных алгебраических уравнений.

Метод Крамера.

Если для системы n уравнений с n неизвестными

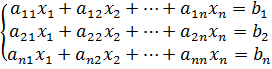      (2)

 

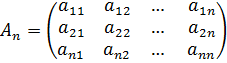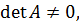,  то система (2) имеет единственное решение, которое находится по формулам Крамера:

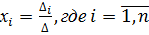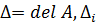, - определители n-го порядка, которые получаются из  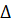путем замены i-го столбца столбцом свободных членов  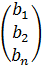исходной системы.

Матричный метод.

Рассмотрим систему n уравнений с n неизвестными (2). Обозначим

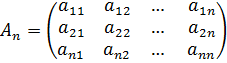 - основная матрица,  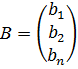- матрица-столбец свободных членов,  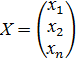- матрица столбец неизвестных.

Тогда система (2) может быть записана в матричной форме: АХ=В

Умножив это матричное уравнение слева на 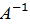, получим:

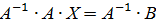т.к.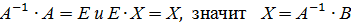

Следовательно, чтобы найти матрицу-решение Х, надо найти 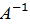 и умножить её на матрицу В.

Надо помнить, что для матрицы А существует единственная обратная матрица 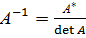, если 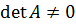, т.е. матрица не вырожденная.

1.3.3 Метод Гаусса.

Рассмотрим систему m уравнений с n неизвестными

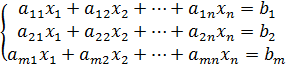      (3)

Введем обозначение:

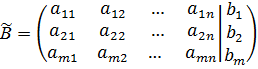 - расширенная матрица для системы (3)

С помощью элементарных преобразований матрица 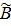 сводится к «треугольному» виду, т.е. под элементами главной диагонали должны быть нули.

Далее записываем систему уравнений, соответствующих последней матрице, эквивалентной исходной. Двигаясь снизу вверх, последовательно находим неизвестные.

Метод Гаусса позволяет решать системы, имеющие единственное решение, бесконечное множество решений и определять, что система решений не имеет.

Историческая справка.

Метод последовательного исключения неизвестных для нахождения решений системы линейных уравнений опубликован в 1849 году немецким математиком, физиком и астрономом Карлом Фридрихом Гауссом (1777-1855). Но уже во 2 в. до н.э. в Китае был известен метод «фан-чен» решение системы n линейных уравнений с n неизвестными, по существу совпадающий с методом Гаусса, от которого он отличается тем, что все операции проводится на счетной доске (само название «фан-чен» переводится как «выстраивание чисел по клеткам»). Правильное расположение чисел на доске заменяло китайскому математику буквы и индексы нашей символики.

 

Решение типового варианта.

Задача 1.

Даны матрицы А, В, С, числа .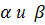

 Вычислить: а)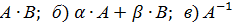

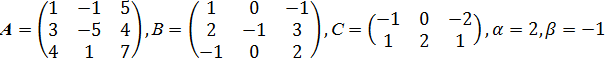
а)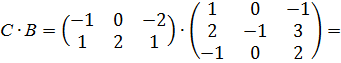

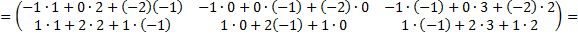
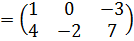
б)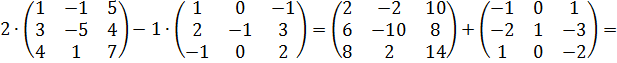

 

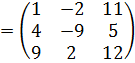
в)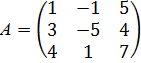

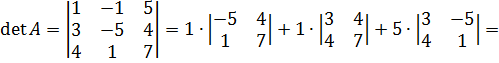
=-35-4+21-16+5(3+20)=-55+21+115=81 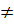0

Найдем алгебраические дополнения 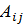 элементов  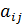матрицы А:

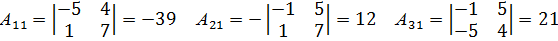
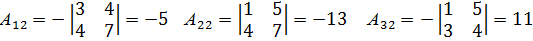
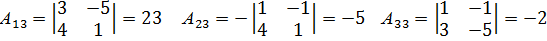
Присоединенная матрица

 

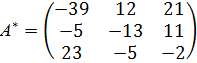
Обратная матрица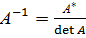

 

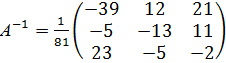
Проверка:

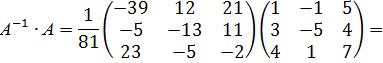
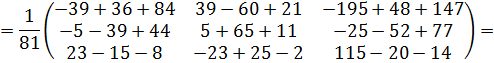
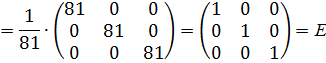
Обратная матрица найдена верно.

 

Задача 2.

  Решить системы линейных уравнений

а) по формулам Крамера, матричным методом, методом Гаусса;

б) методом Гаусса;

в) методом Гаусса.

 

а)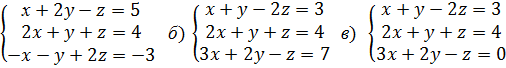

 

Решение:

а) 1. Решим систему методом Крамера.

 

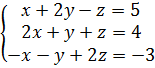
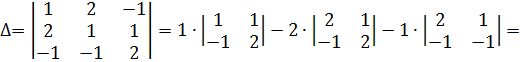
=2+1-2(4+1)-(-2+1)=3-10+1=-6

 

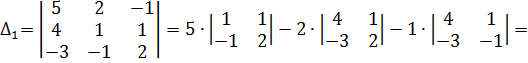
=5(2+1)-2(8+3)-(-4+3)=15-22+1=-6

 

=8+3-5(4+1)-1(-6+4)=11-25+2=-12

 

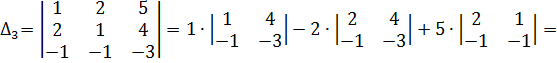
=-3+4-2(-6+4)+5(-2+1)=1+4-5=0

 

 

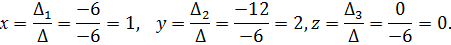
Чтобы проверить решение, подставим в исходную систему уравнений найденные значения неизвестных.

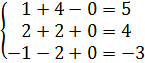
Получены верные равенства, система решена правильно.

Ответ: x=1, y=2, z=0.

 

2. Решим систему матричным методом.

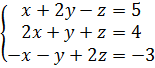
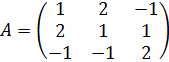 - основная матрица

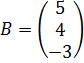 – матрица-столбец свободных членов

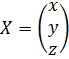 - матрица-столбец неизвестных

Запишем систему уравнений в матричном виде: AX=B.

Умножим обе части уравнения слева на  :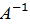

 

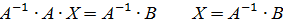
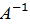 существует, т.к. .

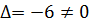Найдем алгебраические дополнения 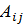 элементов  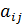матрицы А:

 

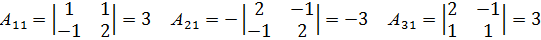
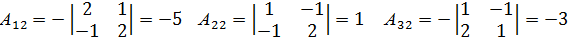
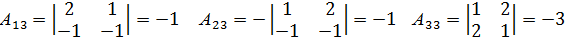
Присоединенная матрица

 

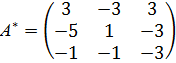
Обратная матрица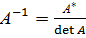

 

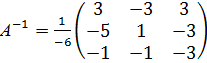
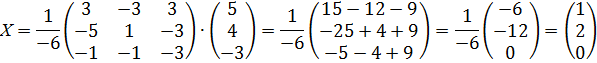
Ответ: x=1, y=2, z=0.

3. Решим систему методом Гаусса.

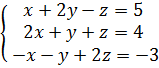
Запишем расширенную матрицу и элементарными преобразованиями сведём её к «треугольному» виду:

    «2 стр.» + «1 стр.» (-2)              «2 стр.»  3

       «3 стр.» + «1 стр.»

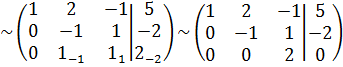
    «3 стр.» + «2 стр.»

Полученной матрице соответствует следующая система уравнений:

 

 

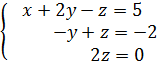
Решим уравнения, двигаясь снизу вверх

1) 2z=0      2) -y+z=-2      3)x+2y-z=5

z=0        -y+0=-2              x+4-0=5

                 y=2         x=1

Ответ: x=1, y=2, z=0.

 

б)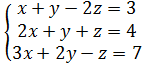

Решим систему методом Гаусса.

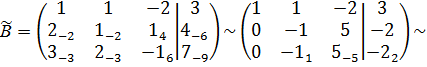
    «2 стр.» + «1 стр.» 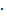(-2)    «3 стр.» + «2 стр.» 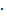(-1)

       «3 стр.» + «1 стр.» 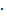(-3)

 

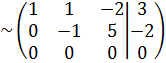
Система 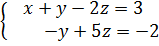имеет бесконечное множество решений, количество уравнений (m=2) меньше чем количество неизвестных (n=3).

n-m=3-2=1

Одно неизвестное обозначим как произвольный параметр t, оставшиеся 2 через него выразим.

 

Пусть z=t тогда

-y+5t=-2         x+y-2z=3

-y=-5t-2          x+5t+2-2t=3

y=5t+2            x=1-3t

Бесконечное множество решений системы запишем следующим образом:

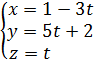 где .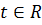

Покажем, что формулы нахождения решений получены правельно.

Пусть t=0, тогда 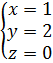подставим в исходную систему:

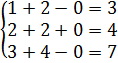
Получили верные равенства, значит решение выполнено правильно.

Ответ: Система имеет бесконечное множество решений: 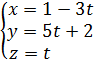 где .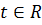

в) 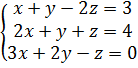 Решим систему методом Гаусса.

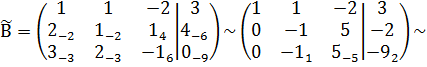
     «2 стр.» + «1 стр.» 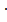 (-2)   «3 стр.» + «2 стр.»  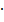(-1)

      «3 стр.» + «1 стр.» 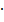 (-3)

 

 

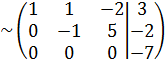
Матрице соответствует следующая система уравнений:

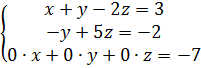
Последнее уравнение не имеет решений ни при каких значениях x,y,z, значит и система решений не имеет.

Ответ: Система не имеет решений.