2020-05-12
101
Векторная алгебра.
Сложение векторов. Умножение вектора на скаляр.
Вектором называется направленный отрезок 
, в котором точка А рассматривается как начало, а точка В - как конец вектора.
Модуль (длина) вектора обозначается 
В параллелограмме, построенном на данных и 
, одна вектор – диагональ есть сумма векторов 
а другая вектор-диагональ есть разность векторов 
.
Произведением вектора 
на число (скаляр) m называется вектор, имеющий длину 
и направленный одинаково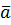 
с (при m > 0) или противоположно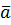
(при m<0).
Если известны координаты начала А 
и конца вектора В 
, то координаты вектора можно найти по правилу
, 
координаты середины отрезка АВ:
Если векторы заданы в координатной форме 
, 
, 
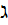- константа, то
1) 
- координаты суммы (разности) векторов;
2) 
- координаты произведения вектора на число;
3) 
- длина вектора .
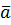Скалярное произведение двух векторов.
Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
|
|
|
Свойства скалярного произведения:
1. 
- переместительный закон.
2. 
– распределительный закон.
3. 
, поэтому 
4. Если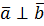 
, то 
5. Если векторы заданы координатами и , то 
Угол между векторами:
Условие коллинеарности векторов 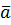и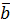 
:
Условие ортогональности векторов 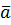и :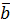
Векторное произведение двух векторов.
Определение: Векторным произведением вектора 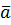на вектор 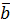, называется вектор, обозначаемый 
и определяемы следующими тремя условиями:
1) 
;
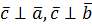2) , , 
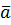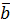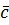образуют правую тройку, т.е. из конца третьего вектора движение первого ко второму по кратчайшему пути наблюдается против часовой стрелки;
3) 
, где 
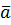- угол между векторами и .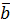
Свойства векторного произведения:
1. 
2. 
3. Если 
то 
Векторные произведение векторов:
Если векторы 
заданы в координатной форме и , то 
Площадь параллелограмма, построенного на векторах , численно равна модулю их численного произведения:
.
Площадь треугольника, построенного на векторах :
.
