Определение: Смешенным произведением векторов 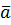 ,
, 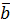 и
и 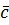 называется выражение вида
называется выражение вида 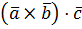 .
.
Если векторы 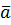 ,
, 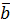 и
и 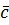 заданы своими координатами, то
заданы своими координатами, то
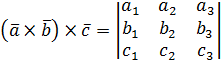 .
.
Свойства смешенного произведения:
1. От перестановки двух соседних сомножителей смешенное произведение меняет знак:
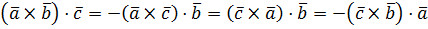 .
.
2. Если два из трех данных векторов равны или коллинеарные, то их смешенное произведение равно нулю.
3. Имеет место тождество 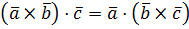 , поэтому смешенное произведение можно записать в виде
, поэтому смешенное произведение можно записать в виде 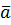
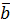
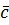 , т.е. без знаков действий и без скобок.
, т.е. без знаков действий и без скобок.
Объем параллелепипеда, построенного на векторах 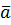 ,
, 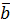 и
и 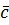 :
:
 .
.
Объем пирамиды, построенной на векторах 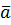 ,
, 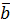 и
и 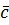 :
:
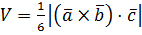 .
.
Условия компланарности трёх векторов:
Если 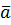 ,
, 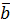 и
и 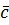 компланарны, то
компланарны, то 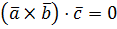 и наоборот.
и наоборот.
Аналитическая геометрия.
Уравнения плоскости.
1.Уравнение плоскости, проходящей через точку 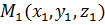 и перпендикулярной к вектору
и перпендикулярной к вектору 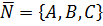 .
.
Пусть 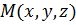 произвольная точка плоскости,
произвольная точка плоскости,
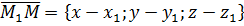
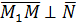 и по условию ортогональности векторов (см. 2.1.2.)
и по условию ортогональности векторов (см. 2.1.2.)
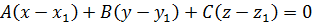 (1)
(1)
2.Общее уравнение плоскости:
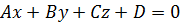 (2)
(2)
Вектор 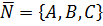 называется нормальным вектором к плоскости (1) и (2).
называется нормальным вектором к плоскости (1) и (2).
3.Уравнение плоскости в отрезках на осях:
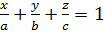 (3)
(3)
Пусть заданы две плоскости Ax+By+Cz+D=0 и 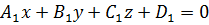
1.Угол, образованный двумя плоскостями равен углу между их нормальными векторами:

2.Условие параллельности плоскостей
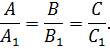
3.Условие перпендикулярности плоскостей:
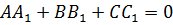
Расстояние точки 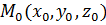 от плоскости Ax+By+Cz+D=0:
от плоскости Ax+By+Cz+D=0:
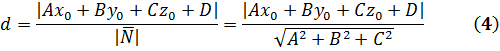
Уравнения прямой в пространстве
1. Уравнения прямой, проходящей через точку 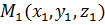 и параллельной вектору
и параллельной вектору 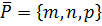 .
.
Пусть 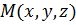 произвольная точка прямой, тогда
произвольная точка прямой, тогда 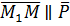 ,
,
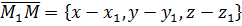 и по условию коллинеарности векторов (см.2.1.2)
и по условию коллинеарности векторов (см.2.1.2)

Уравнения (5) называются каноническими уравнениями прямой.
Вектор 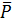 называется направляющим вектором прямой.
называется направляющим вектором прямой.
2. Параметрические уравнения прямой получим, приняв каждое из отношений (5) параметру t:
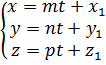 (6)
(6)
3. Уравнения прямой, проходящей через две точки 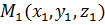 и
и 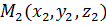 :
:

4.Общие уравнения прямой:

Угол между прямой 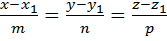 и плоскостью Ax+By+Cz+D=0
и плоскостью Ax+By+Cz+D=0

Уравнения прямой на плоскости.
Уравнения прямой с угловым коэффициентом.

Угловой коэффициент 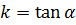 , где -
, где - 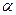 угол наклона прямой к оси ОХ.
угол наклона прямой к оси ОХ.
Общее уравнение прямой
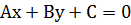
 2020-05-12
2020-05-12 183
183








