2020-05-12
102
Драчева И.А., Ершова Т.Г.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Часть
Практикум
По самостоятельной работе и выполнению контрольной работы
для студентов направления подготовки 38.03.01 «Экономика»
заочной формы обучения
Керчь, 2016 г.
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ.............................................................................................. | 4 |
| ТАБЛИЦА ВЫБОРА ВАРИАНТА ЗАДАНИЙ …………………….. | 5 |
| ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ….. ………………………. | 5 |
| РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ И ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ …... | 9 |
| 1 Предел функции. Задание 1-10………….……….......................... | 9 |
| 2 Непрерывность функции. Точки разрыва. Задание 11-20…………. | 12 |
| 3 Производная функции. Задание 21-30…………………………….. | 13 |
| 4 Исследование функций. Задание 31-40…………………………… | 16 |
| 5 Неопределенный интеграл. Задание типа 41-50………………….. | 21 |
| ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ…………………… | 26 |
| СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ | 27 |
ВВЕДЕНИЕ
|
|
|
Цель преподавания математики для студентов экономических направлений ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач экономики; развить их логическое мышление; привить студентам навыки самостоятельного изучения литературы по математике; повысить общий уровень математической культуры.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом по математическим дисциплинам. Она складывается из чтения учебников, методических пособий, решения задач, выполнения контрольных заданий.
Настоящее пособие содержит вопросы для подготовки к экзамену (зачету) по математическому анализу, контрольные задания и методические указания к решению задач за 1 семестр.
При выполнении контрольных работ студент должен следовать следующим рекомендациям:
- Каждую работу необходимо выполнять в отдельной тетради, на обложке которой должны быть указаны номер контрольной работы, фамилия и инициалы студента, полный шифр, дата отсылки работы в университет.
- При решении задач необходимо указать номер задачи и ее содержание. Решение задачи должно сопровождаться достаточно подробными пояснениями.
- Все вычисления должны быть приведены полностью, чертежи и графики выполнены аккуратно.
- Для удобства рецензирования преподавателем контрольной работы следует на каждой странице оставлять поля.
После получения из университета отрецензированной работы студент должен исправить в ней все ошибки. Если работа не допущена к защите, то в кратчайший срок студенту необходимо после устранения замечаний преподавателя представить работу на повторное рецензирование. Ошибки следует исправлять в той же тетради.
|
|
|
Перед экзаменом или зачетом студент должен защитить контрольную работу. Защита предполагает проверку того, что работа выполнена студентом самостоятельно. Поэтому при защите студент должен быть готов дать пояснения к решенным задачам или решить подобные задачи.
На экзамен (или зачет) необходимо представить преподавателю все запланированные контрольные работы.
Студент выполняет в первом семестре по математическому анализу одну контрольную работу, вариант контрольной работы совпадет с последней цифрой его учебного шифра.
ТАБЛИЦА ВЫБОРА ВАРИАНТА ЗАДАНИЙ
| Вариант | Номера задач контрольных заданий | Вариант | Номера задач контрольных заданий | ||||||||
| 1 | 1 | 11 | 21 | 31 | 41 | 6 | 6 | 16 | 26 | 36 | 46 |
| 2 | 2 | 12 | 22 | 32 | 42 | 7 | 7 | 17 | 27 | 37 | 47 |
| 3 | 3 | 13 | 23 | 33 | 43 | 8 | 8 | 18 | 28 | 38 | 48 |
| 4 | 4 | 14 | 24 | 34 | 44 | 9 | 9 | 19 | 29 | 39 | 49 |
| 5 | 5 | 15 | 25 | 35 | 45 | 10 | 10 | 20 | 30 | 40 | 50 |
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
1-10. Найти предел функции, не используя правило Лопиталя.
| 1. | 1)  ;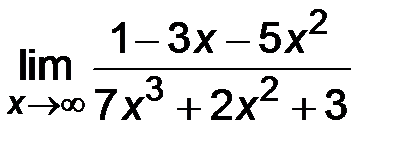
| 2)  ;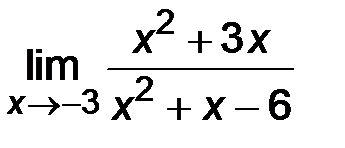
| 3)  ;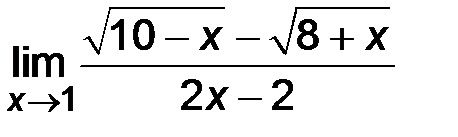
|
4)  ;
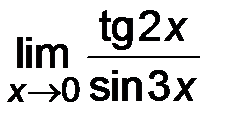| 5)  .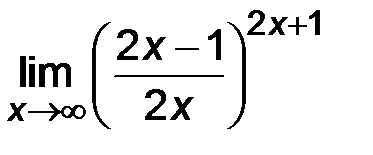
| ||
| 2. | 1)  ;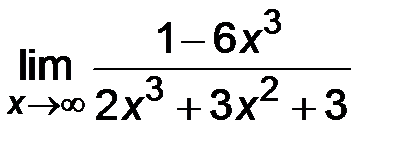
| 2)  ;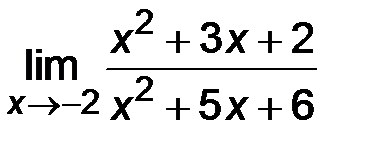
| 3)  ;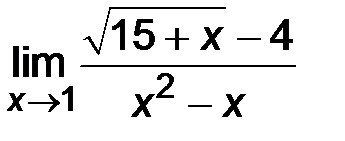
|
4)  ;
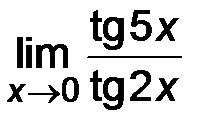| 5)  .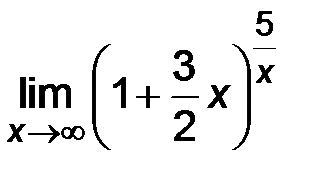
| ||
| 3. | 1)  ;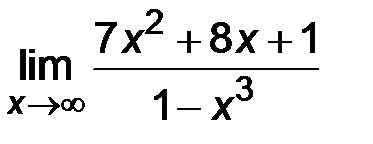
| 2)  ;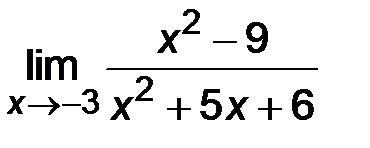
| 3)  ;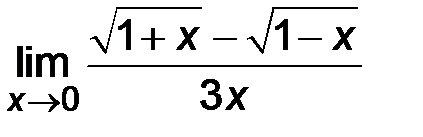
|
4)  ;
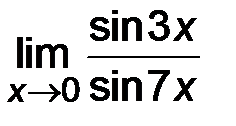| 5)  .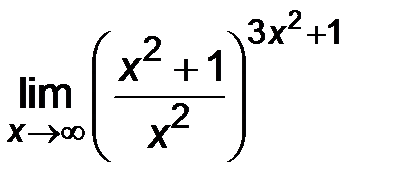
| ||
| 4. | 1)  ;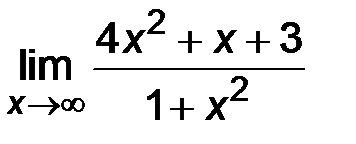
| 2)  ;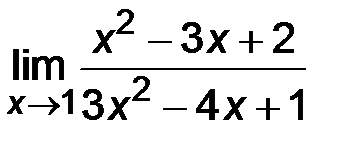
| 3)  ;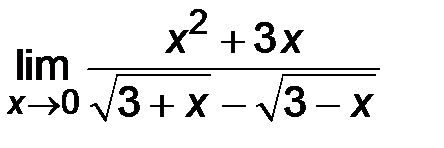
|
4)  ;
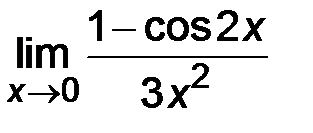| 5)  .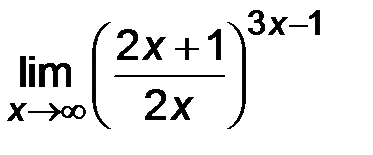
| ||
| 5. | 1)  ;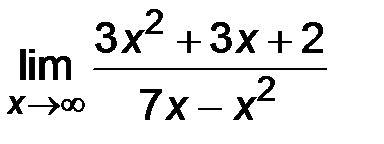
| 2)  ;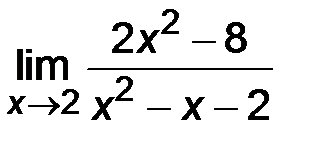
| 3)  ;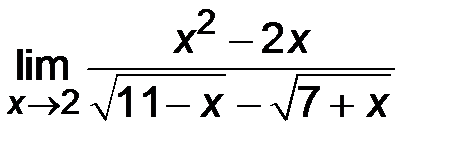
|
4)  ;
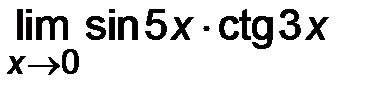| 5)  .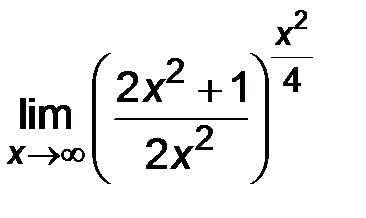
| ||
| 6. | 1)  ;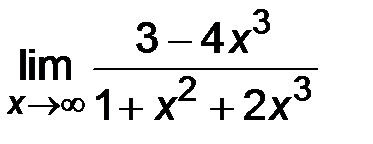
| 2)  ;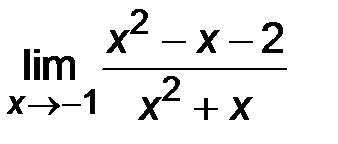
| 3)  ;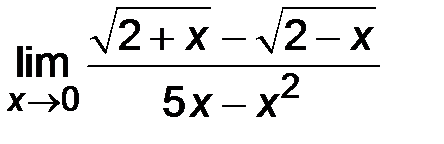
|
4)  ;
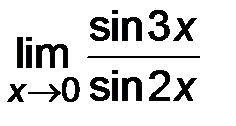| 5)  .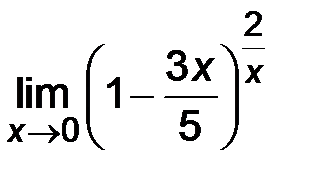
| ||
| 7. | 1)  ;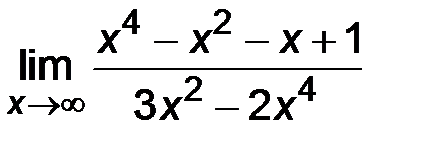
| 2)  ;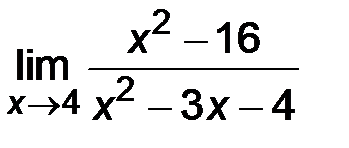
| 3)  ;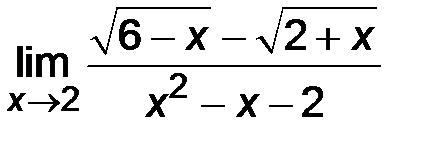
|
4)  ;
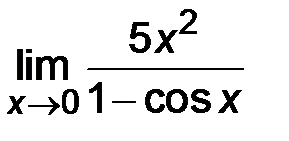| 5)  .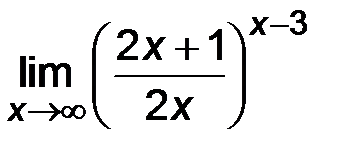
| ||
| 8. | 1)  ;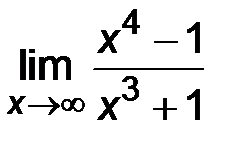
| 2)  ;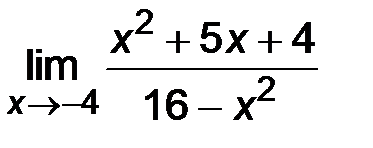
| 3)  ;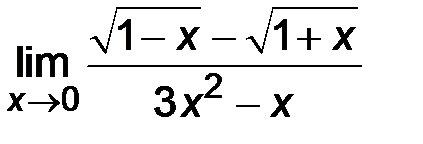
|
4)  ;
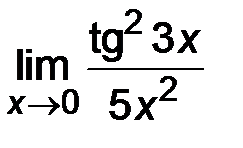| 5)  .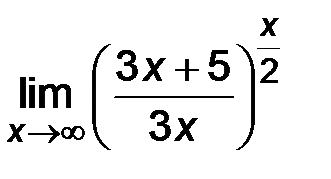
| ||
| 9. | 1)  ;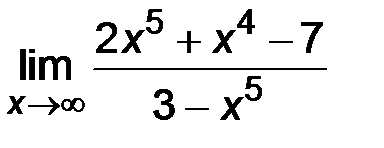
| 2)  ;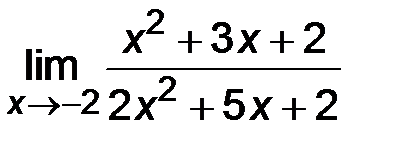
| 3)  ;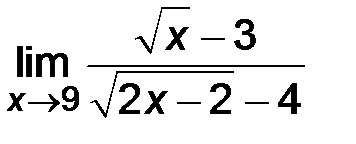
|
4)  ;
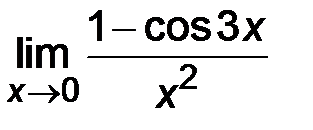| 5)  .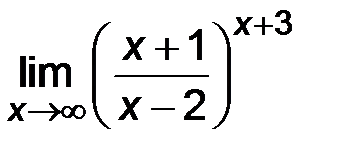
| ||
| 10. | 1)  ;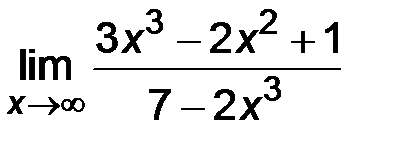
| 2)  ;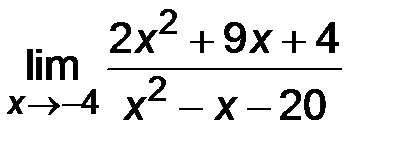
| 3)  ;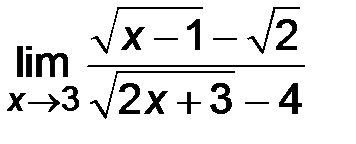
|
4)  ;
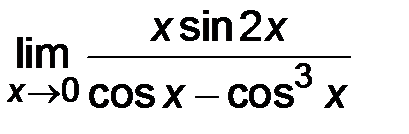| 5)  .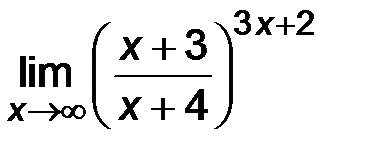
|
11-20. Найти все точки разрыва функции y = f(x). Построить график функции.
11. 
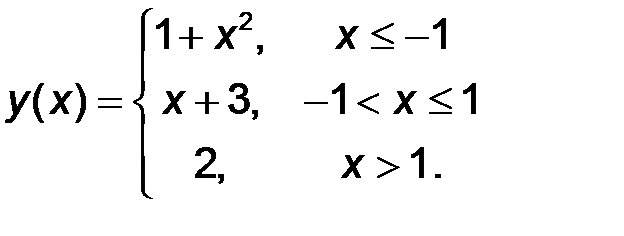
| 12.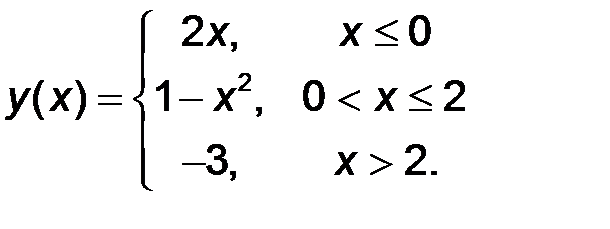 
| |
13. 
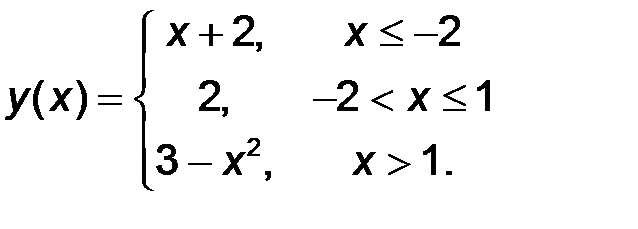
| 14.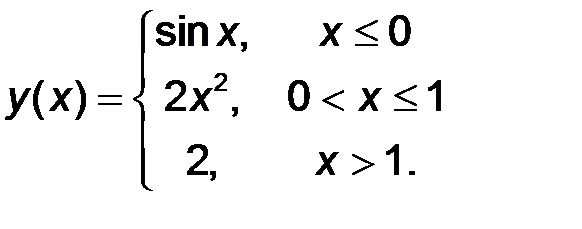 
| |
15. 
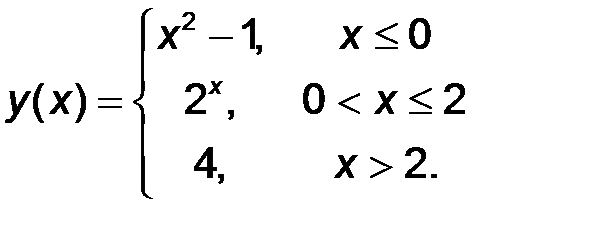
| 16.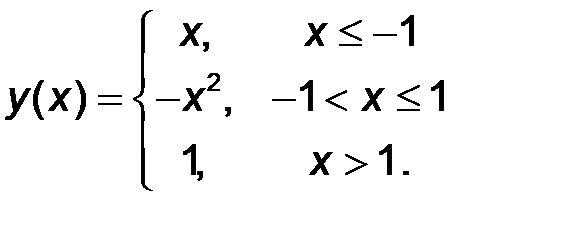 
| |
17. 
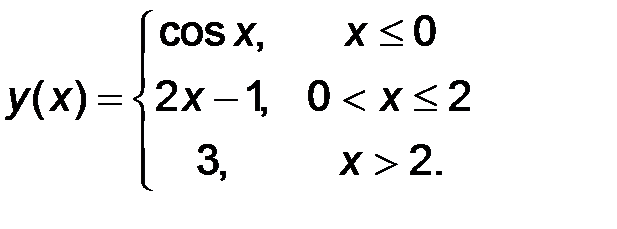
| 18.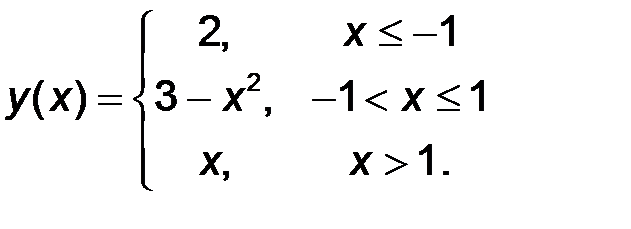 
| |
19. 
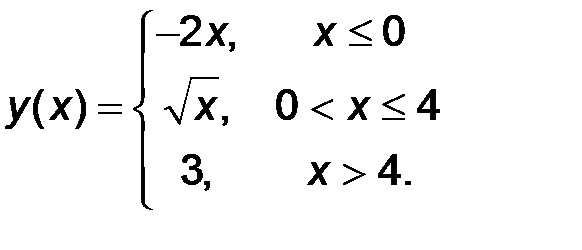
| 20.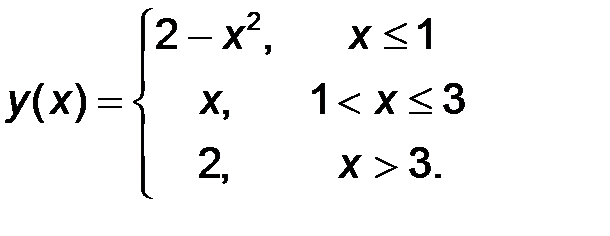 
|
21-30. Найти производную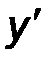 
функции y = f(x).
| 21. | 1)  ;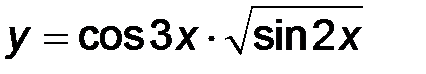
| 2)  ;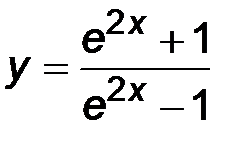
|
3)  ;
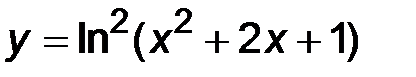| 4)  .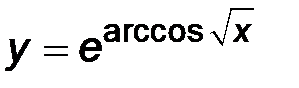
| |
| 22. | 1)  ;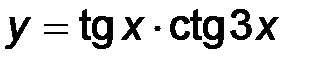
| 2)  ;
|
3)  ;
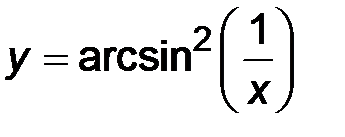| 4)  .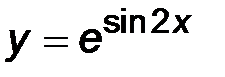
| |
| 23. | 1)  ;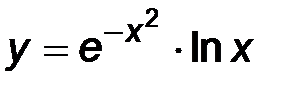
| 2)  ;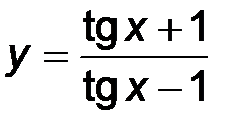
|
3) 
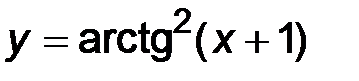
| 4)  .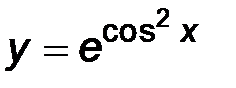
| |
| 24. | 1)  ;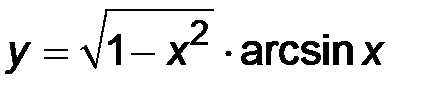
| 2)  ;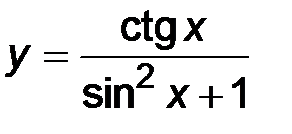
|
3)  ;
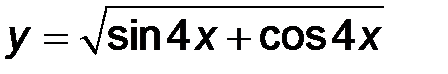| 4)  .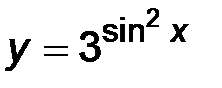
| |
| 25. | 1)  ;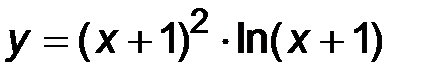
| 2)  ;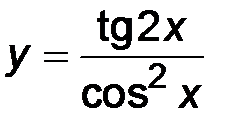
|
3)  ;
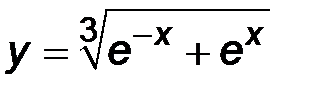| 4)  .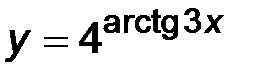
| |
| 26. | 1)  ;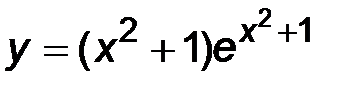
| 2)  ;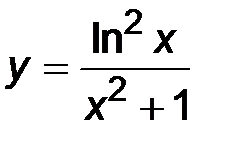
|
3)  ;
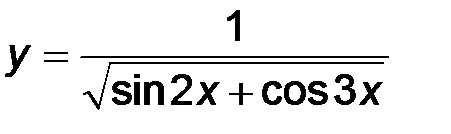| 4)  .
| |
| 27. | 1)  ;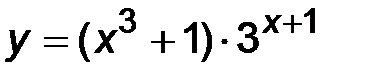
| 2)  ;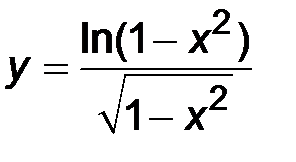
|
3)  ;
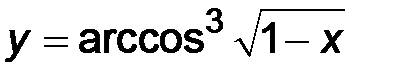| 4)  .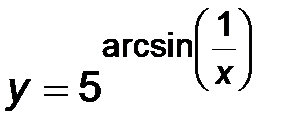
| |
| 28. | 1)  ;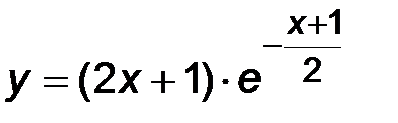
| 2)  ;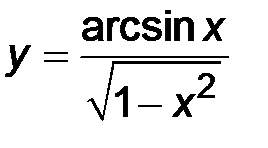
|
3)  ;
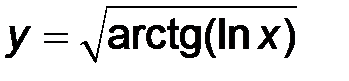| 4)  .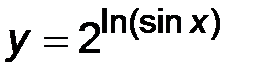
| |
| 29. | 1)  ;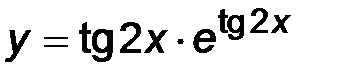
| 2)  ;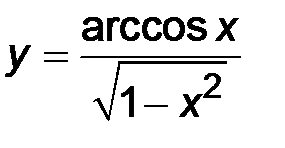
|
3)  ;
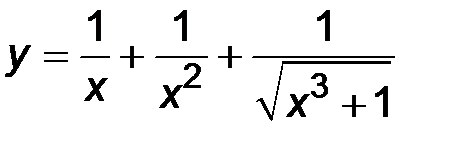| 4)  .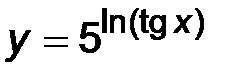
| |
| 30. | 1)  ;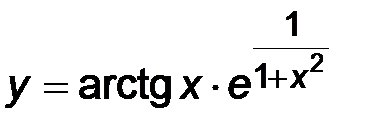
| 2)  ;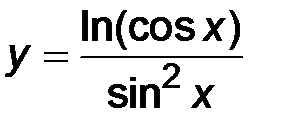
|
3)  ;
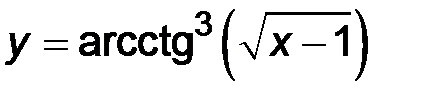| 4)  .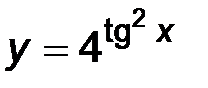
|
31-40. Исследовать методами дифференциального исчисления функцию y = f(x) и построить ее график.
31. 
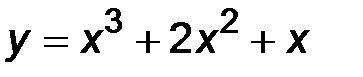
| 32.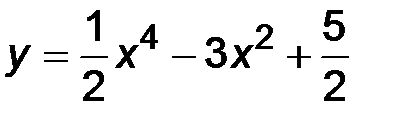 
|
33. 
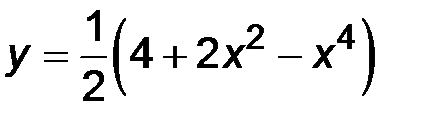
| 34.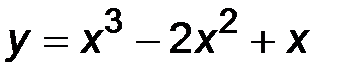 
|
35. 
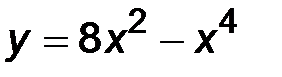
| 36.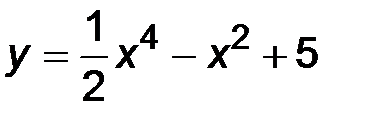 
|
37. 
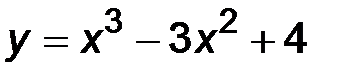
| 38.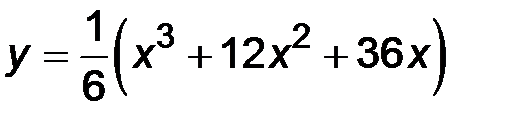 
|
39. 
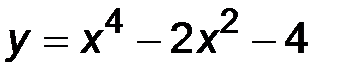
| 40.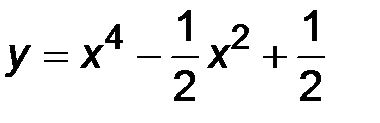 
|
41-50. Найти неопределенные интегралы.
| 41. | а)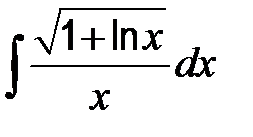 
| б)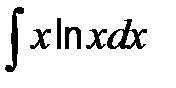 
| в)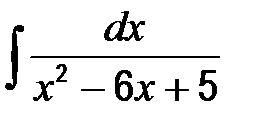 
| г)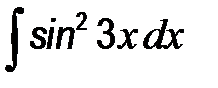 
|
| 42. | а)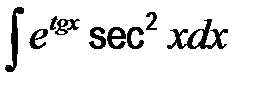 
| б)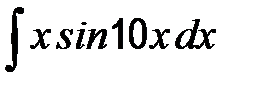 
| в)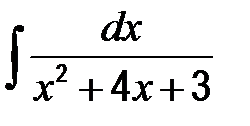 
| г)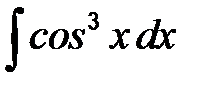 
|
| 43. | а)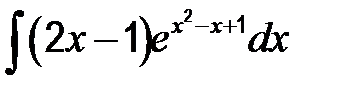 
| б)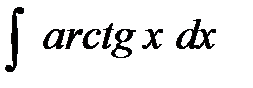 
| в)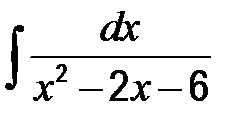 
| г)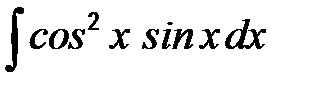 
|
| 44. | а)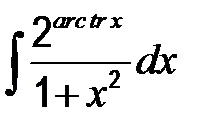 
| б)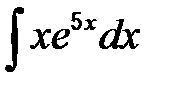 
| в)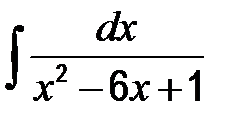 
| г)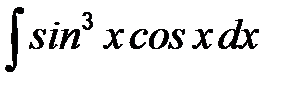 
|
| 45 | а)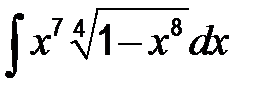 
| б)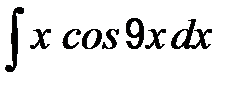 
| в)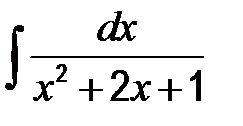 
| г)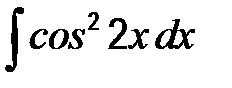 
|
| 46. | а)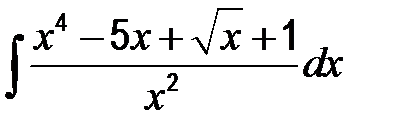 
| б)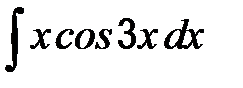 
| в)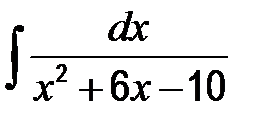 
| г)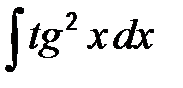 
|
| 47. | а)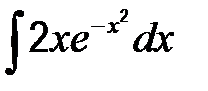 
| б)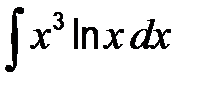 
| в)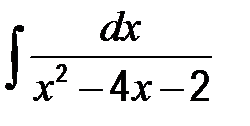 
| г)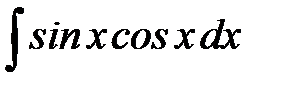 
|
| 48. | а)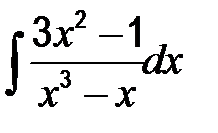 
| б)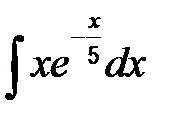 
| в)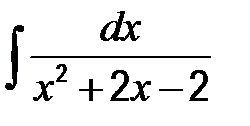 
| г)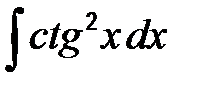 
|
| 49. | а)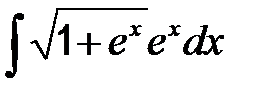 
| б)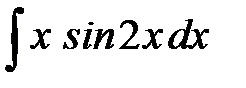 
| в)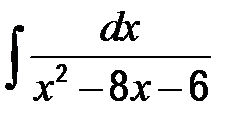 
| г)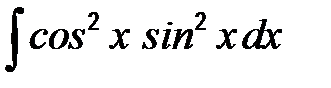 
|
| 50. | а)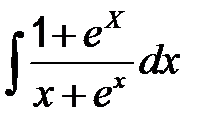 
| б)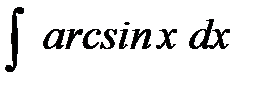 
| в)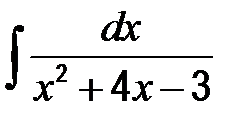 
| г)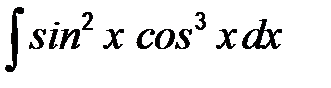 
|
РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ И ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Предел функции. Задание 1-10
Найти предел функции, не используя правило Лопиталя.
1)  ;
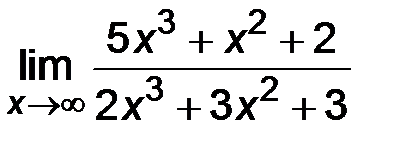| 2)  ;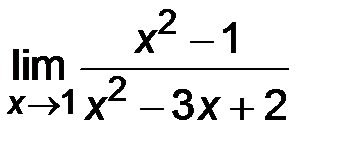
| 3)  ;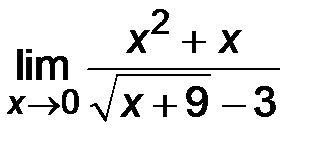
|
4)  ;
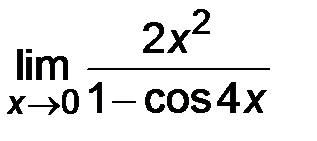| 5)  .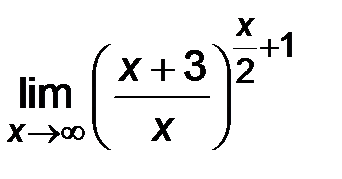
|
Для отыскания предела функции y = f(x) обычно используют теоремы о конечных пределах, из которых следует, что если предельная точка x 0 входит в область определения функции y = f(x), то для его отыскания нужно найти значение функции y = f(x) в точке x=x 0.
Например,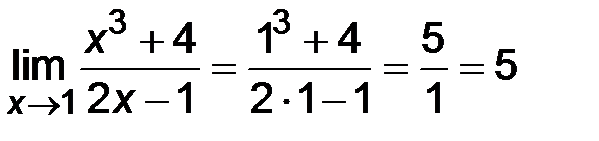 
.
Теоремы о конечных пределах нельзя применять, если при подстановке вместо x значения x 0 в функцию y = f(x) получаем неопределенные выражения или неопределенности вида:
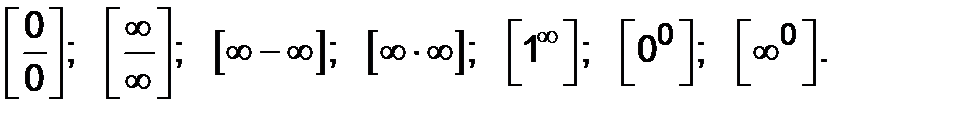
Чтобы найти предел функции, необходимо раскрыть неопределенность. Рассмотрим основные методы раскрытия неопределенностей на примерах.
1) .
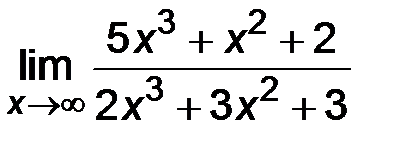Решение.
Функция y =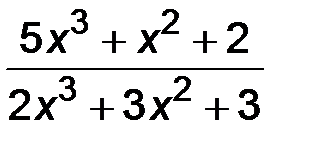 
представляет собой частное двух функций, но теорему о пределе частного применять нельзя, т.к. при х ® ¥ числитель и знаменатель неограниченно возрастают. Имеем неопределенность вида 
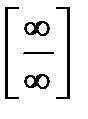. Выделим переменную х в высшей степени и разделим числитель и знаменатель на нее. В данном примере разделим числитель и знаменатель на х3, затем перейдем к пределу.
.
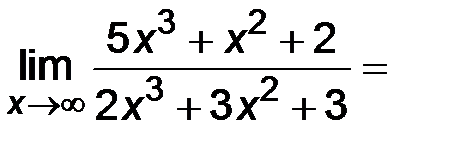
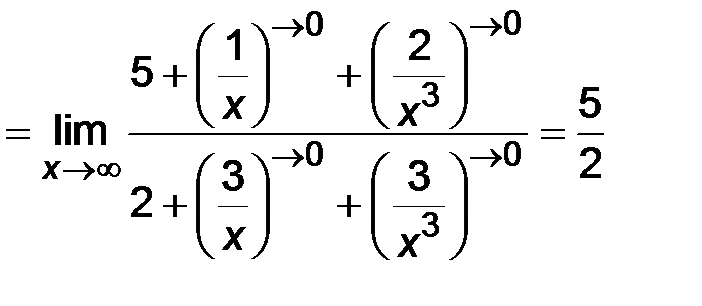2) ;
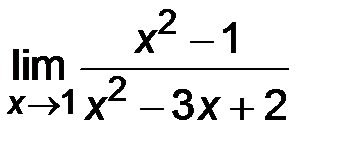Решение.
В данном случае при подстановке х = 1 в числитель и знаменатель функции получим неопределенность вида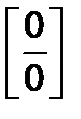 
. В подобных примерах, когда числитель и знаменатель многочлены, необходимо разложить их на множители, после чего сократить дробь и перейти к пределу. Если х1, х2 – корни квадратного трехчлена y = 
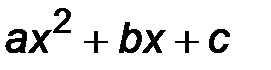, то его можно представить иначе: 
.
|
|
|
.
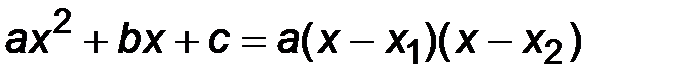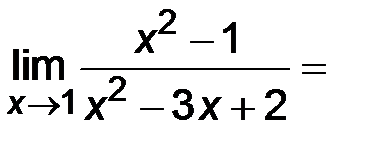
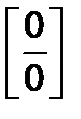
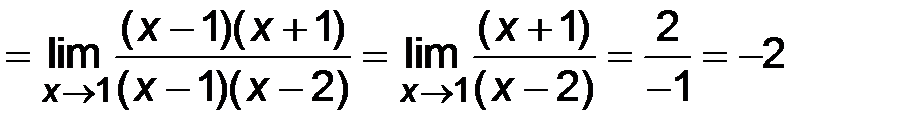3) ;
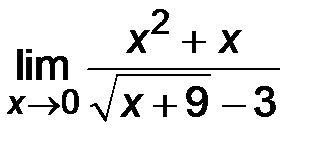Решение.
При подстановке х=0 в функцию получим неопределенность вида 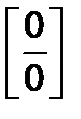. В данном примере под знаком предела имеется иррациональность. Поэтому для раскрытия неопределенности числитель и знаменатель умножают на выражение, сопряженное иррациональному, затем дробь сокращают и переходят к пределу.
.
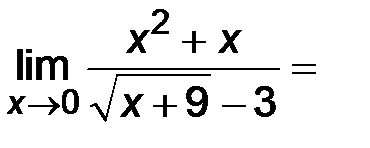
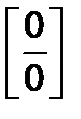
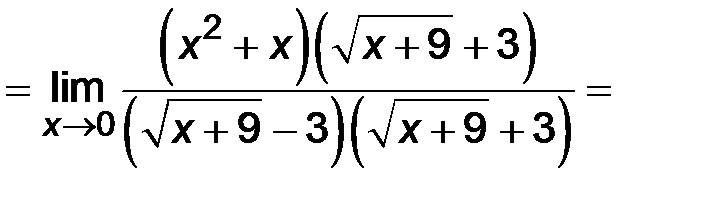
4) ;
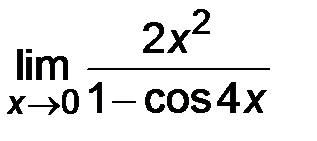Решение. В данном примере имеем неопределенность вида 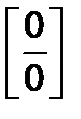с тригонометрическими функциями. Для раскрытия неопределенности используется первый замечательный предел:
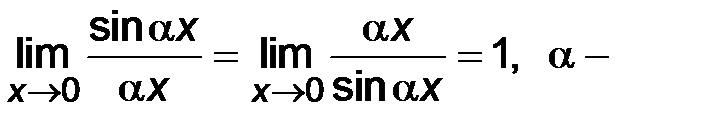действительное число.
Знаменатель дроби преобразуем по формуле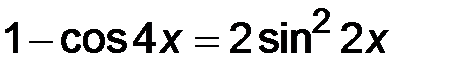 
.
.
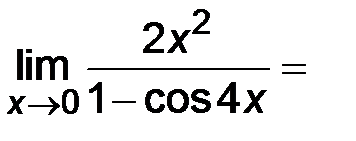
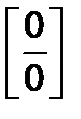
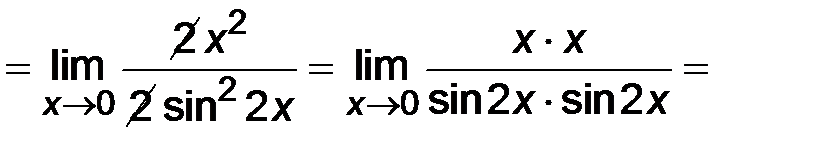
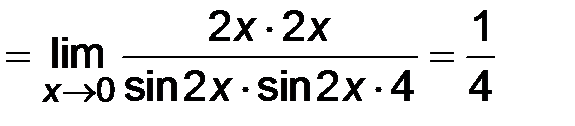5) 
.
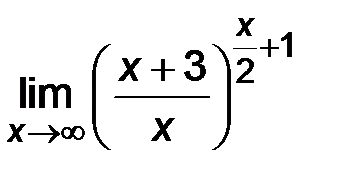Решение.
В данном примере имеем неопределенность вида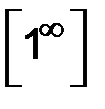 
. Раскроем неопределенность с помощью второго замечательного предела:
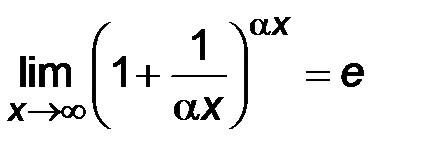или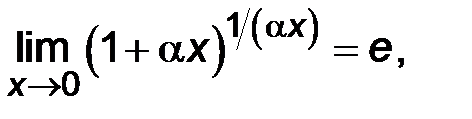 
где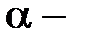 
действительное число;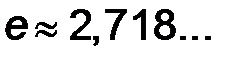 
.
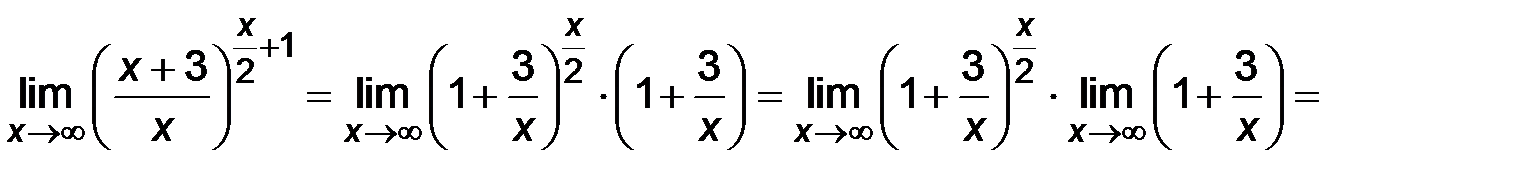
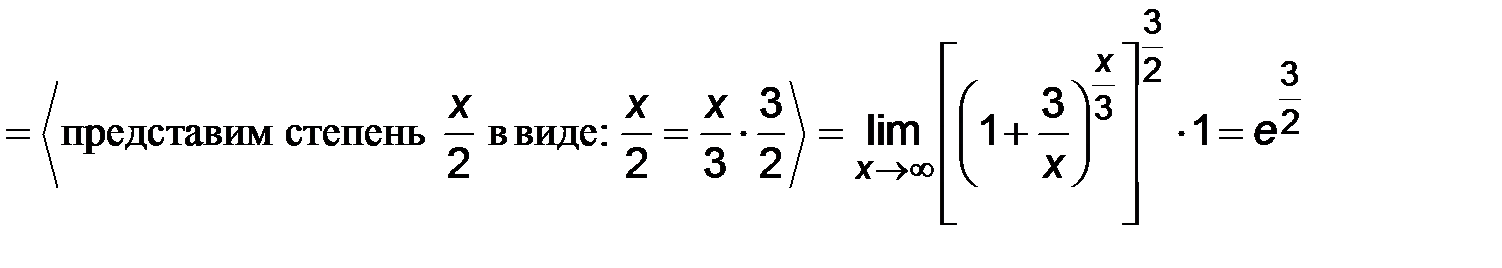Вопросы для самоконтроля.
1. Дайте определение предела функции.
2. Какие функции называются бесконечно малыми, какие бесконечно большими?
3. Сформулируйте основные теоремы о пределах.
4. Какие виды неопределенностей вы можете называть?
5. Как раскрываются неопределенност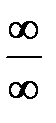и 
и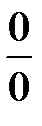 
? Найти пределы: 
; 
.
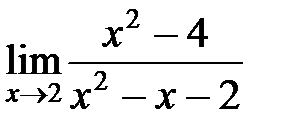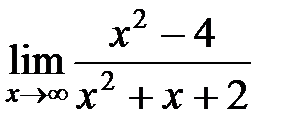Литература: [8] стр. 31-53, [6] стр. 127-149, [10] стр. 131-172.
Примеры: [1] стр. 142; [5] стр. 96-114.
