Неопределенный интеграл
В дифференциальном исчислении одной из основных задач было нахождение производной 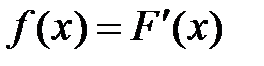 .
.
Рассмотрим обратную задачу: дана производная 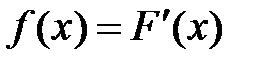 , требуется найти функцию F(x), что является задачей интегрального исчисления.
, требуется найти функцию F(x), что является задачей интегрального исчисления.
Первообразной от функции f (x) называется функция F(x), производная которой равна данной функции, т.е. 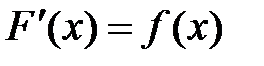 .
.
Если F (x) есть первообразная для функции f (x), то первообразной будет функция F (x) + с, где с – произвольная постоянная, так как 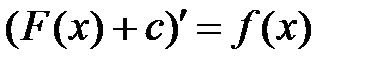 , т.е. первообразных для данной функции существует бесконечное множество.
, т.е. первообразных для данной функции существует бесконечное множество.
Если функция F(x) является первообразной для функции f (x), то выражение F(x) + с называется неопределенным интегралом от функции f (x) и обозначается символом 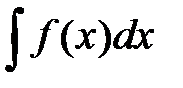 , т.е.
, т.е. 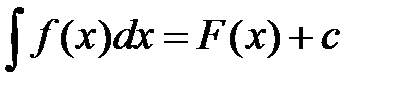 , если
, если 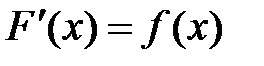 .
.
При этом функция f (x) называется подынтегральной функцией, а f (x) dx подынтегральным выражением. 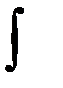 – знак интеграла.
– знак интеграла.
Неопределенный интеграл обладает следующими свойствами:
1) постоянный множитель можно выносить за знак неопределенного интеграла 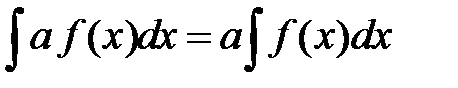 , где а = const;
, где а = const;
2) интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций:
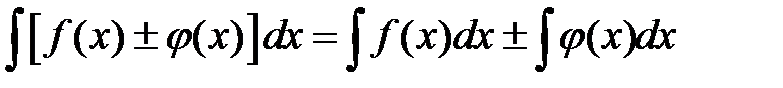
Интегрирование есть действие обратное дифференцированию. Поэтому формулы интегрирования могут быть получены из соответствующих формул дифференцирования.
Таблица основных интегралов
1) 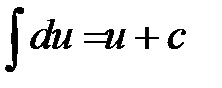 2)
2) 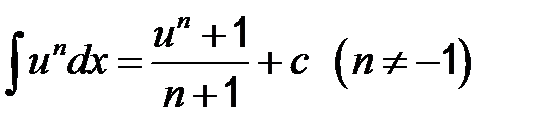
3) 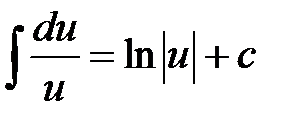 4)
4) 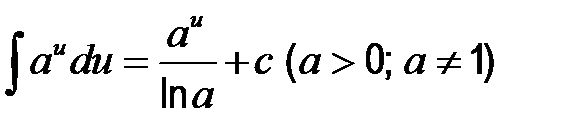
5) 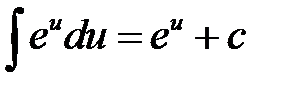 6)
6) 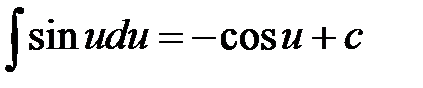
7)  8)
8) 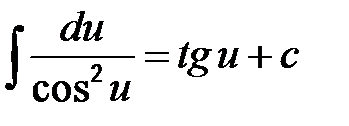
9) 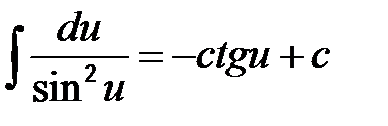 10)
10) 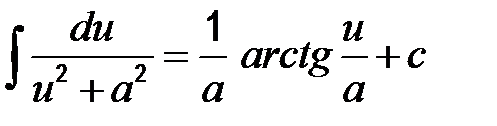
11) 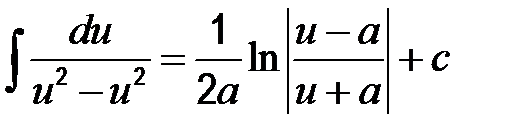 12)
12) 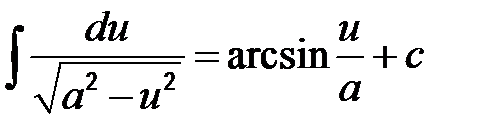
13) 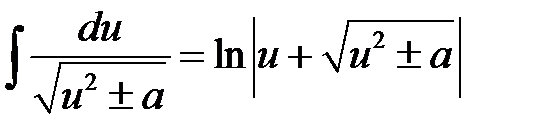
Рассмотрим основные методы интегрирования.
Метод непосредственного интегрирования. Непосредственным интегрированием называется интегрирование, заключающееся в непосредственном применении формул таблицы основных интегралов и использовании их свойств.
Чтобы найти неопределенный интеграл от какой-нибудь функции f(x) нужно прежде всего отыскать в таблице интегралов формулу, в левой части которой будет стоять интеграл того же вида, как данный, и записать ответ в соответствии с правой частью равенства.
Примеры:
1) 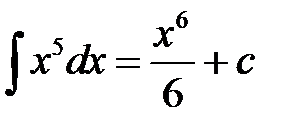 (формула 2);
(формула 2);
2) 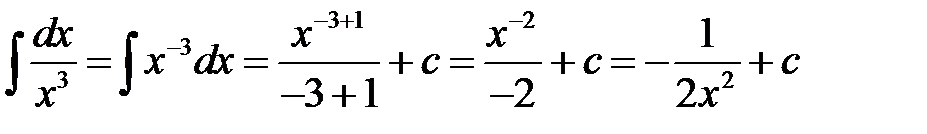 (формула 2);
(формула 2);
3) 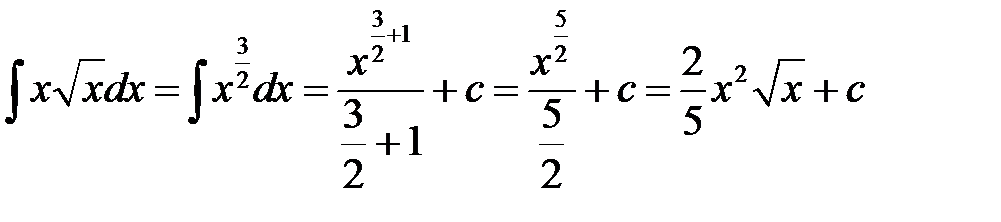 (формула 2);
(формула 2);
4) 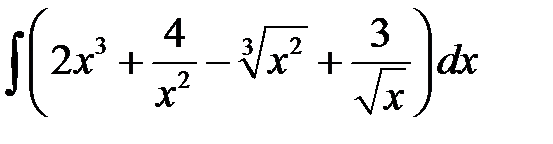 = (используем свойства 1 и 2)=
= (используем свойства 1 и 2)=
= 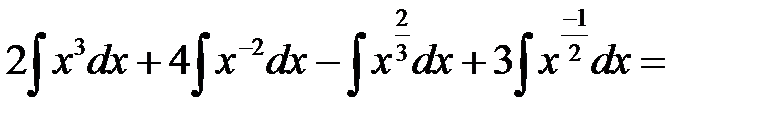 (используем формулу 2)=
(используем формулу 2)=
= 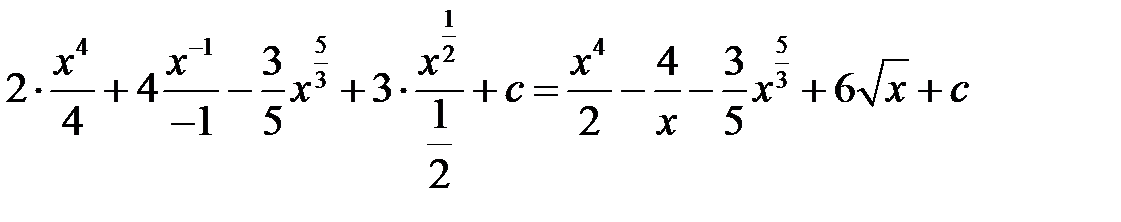 .
.
Правильность результата проверим дифференцированием:
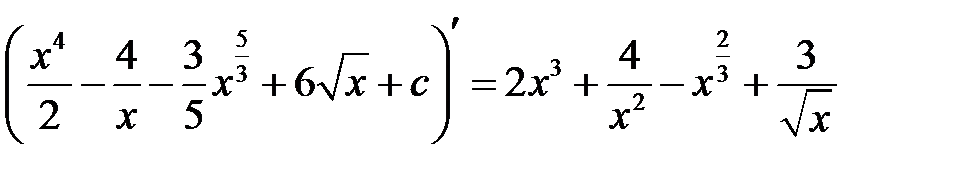
Мы получили подынтегральную функцию
5) 
= 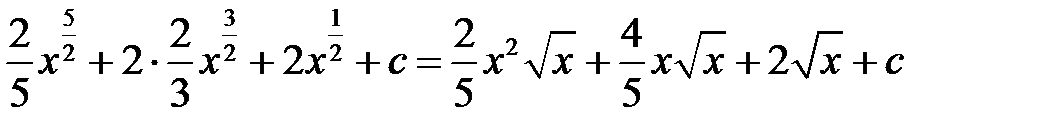
6) 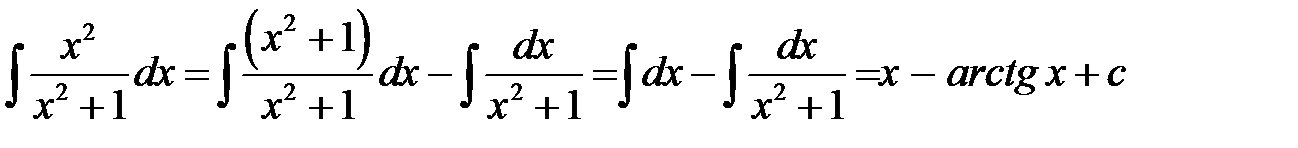 (формулы 1 и 10)
(формулы 1 и 10)
Метод замены переменной (метод подстановки) Наиболее общим приемом интегрирования функций является способ подстановки, который применяется тогда, когда искомый интеграл 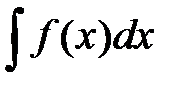 не является табличным, но путем преобразований может быть сведен к табличному.
не является табличным, но путем преобразований может быть сведен к табличному.
Пусть требуется найти интеграл 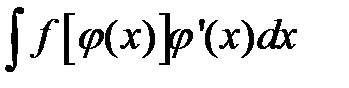 .
.
Применив подстановку 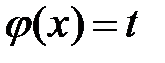 , получим интеграл
, получим интеграл 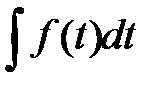 .
.
Примеры:
1) 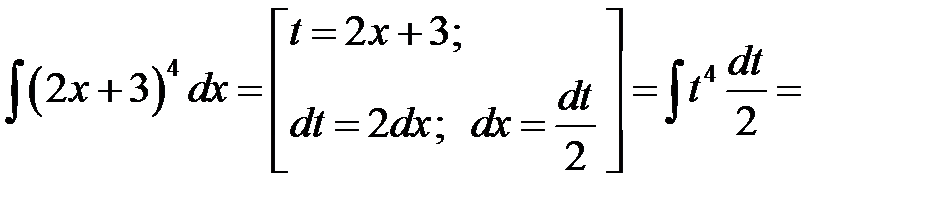
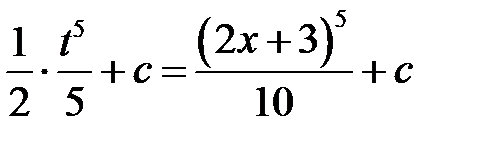 ;
;
2) 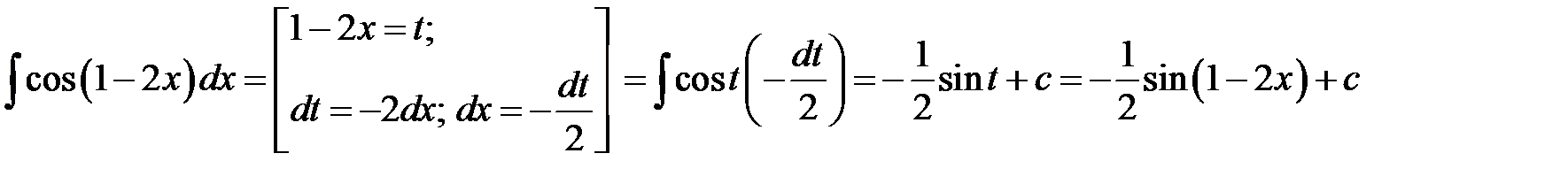
3) 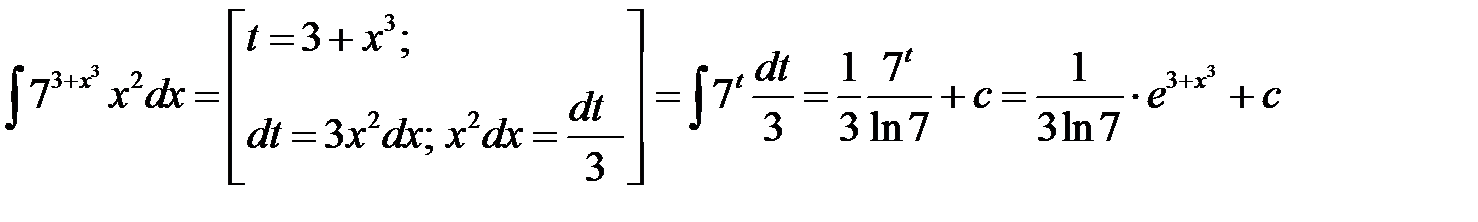 ;
;
4) 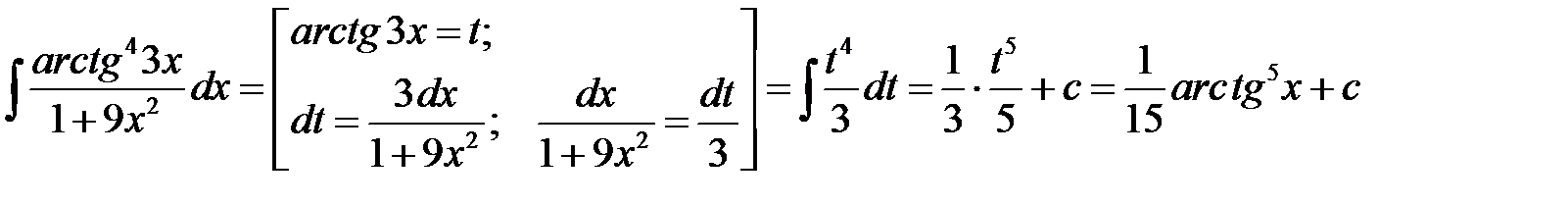 ;
;
5) 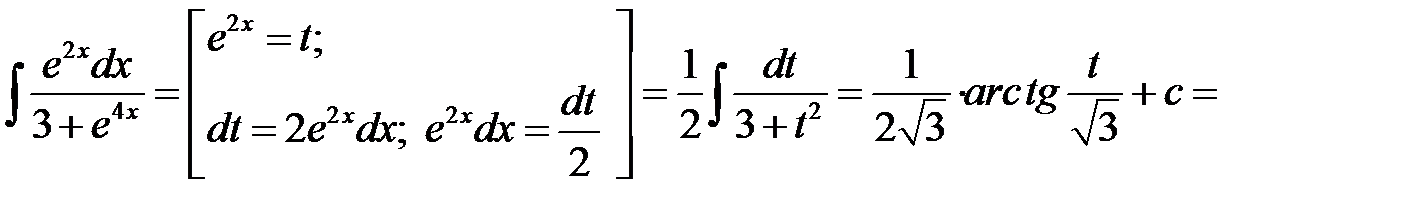
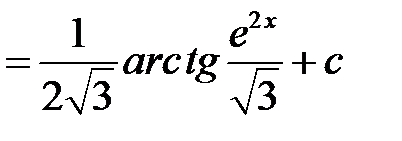
 2020-05-12
2020-05-12 134
134








