2020-05-12
94
Найти производную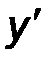 
функции y = f (x).
1. Пусть х 1, х 2 - значения аргумента х, y 1= f (х 1) и y 2= f (х 2) - соответствующие значения функции y = f (x).
Разность 
называется приращением аргумента; разность 
называется приращением функции на отрезке 
.
Производной функции y = f (x) по аргументу х называется предел отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю и этот предел существует. Обозначают производную 
или 
. Следовательно, согласно определения 
.
Операция отыскания производной называется дифференцированием функции.
Геометрический смысл производной:
Производная 
представляет собой угловой коэффициент касательной к графику функции y (x) в точке, абсцисса которой равна x, т.е. 
.
Физический смысл производной:
Производная есть скорость изменения функции. Например, скорость движения материального объекта есть производная от пути по времени, т.е. 
.
2. Свойства производной:
1) Производная постоянной равна нулю: 
2) Производная функции y = x равна единице.
3) Производная суммы функций u (x) и v (x): 
4) Постоянный множитель можно выносить за знак производной:
.
5) Производная произведения функций u (x) и v (x): 
6) Производная частного функций u (x) и v (x): 
7) Производная сложной функции: пусть y = f (u), u = u (x), т.е. y = f [ u (x)], где f (u) и u (x) - дифференцируемые функции. Тогда: 
, т.е. производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
3. Таблица производных основных элементарных функций
| 1 |  
|  
|
| 2 | 
| 
|
| 3 | 
| 
|
| 4 | 
| 
|
| 5 | 
| 
|
| 6 | 
| 
|
| 7 | 
| 
|
| 8 | 
| 
|
| 9 | 
| 
|
| 10 | 
| 
|
| 11 | 
| 
|
| 12 | 
| 
|
| 13 | 
| 
|
| 14 | 
| 
|
Пример 1. Пользуясь правилами и формулами дифференцирования, найти производные функций:
1)  ;
| 2)  ;
| 3)  ;
|
4)  ;
| 5)  .
|
Решение:
1) .
.
2) 
. Переходя к дробным показателям степени, получим:
.
.
3) . Переходя к отрицательным степеням, получим:
.
.
4) . Используем формулу дифференцирования произведения:
.
5) . Используем формулу дифференцирования частного:
.
Пример 2. Найти производную сложной функции:
1)  ;
| 2)  ;
| 3)  ;
|
4)  ;
| 5)  ;
| 6)  .
|
Решение:
1) .
Представим 
в виде цепочки функций: 
.
.
2) . 
.
.
3) . 
.
4) . 
.
5) . 
.
6) . 
Вопросы для самоконтроля.
1. Дайте определение производной функции.
2. Как обозначается производная?
3. Назовите свойства производной.
4. Расскажите правила дифференцирования функций.
5. Напишите формулы дифференцирования основных элементарных функций.
6. Какие функции называются сложными?
7. Как найти производную сложной функции?
Литература: [6] стр. 167-177, [8] стр. 68-96, [10] стр. 186-201.
Примеры: [1] стр.151-166; [5] стр116-133.
