Построение графиков. Кусочная функция

а) y =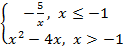     

1) Постройте график функции обратной пропорциональности y = 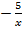 на промежутке

x	-1	-2	-2,5	-5
y	2,5	2,5	2	1

 

2) Постройте график квадратичной функции 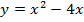 на промежутке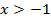

 =  =

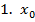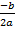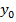 (2) = -4

   (2; -4) – вершина параболы

2. Ветви параболы вверх, т.к. a 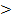0

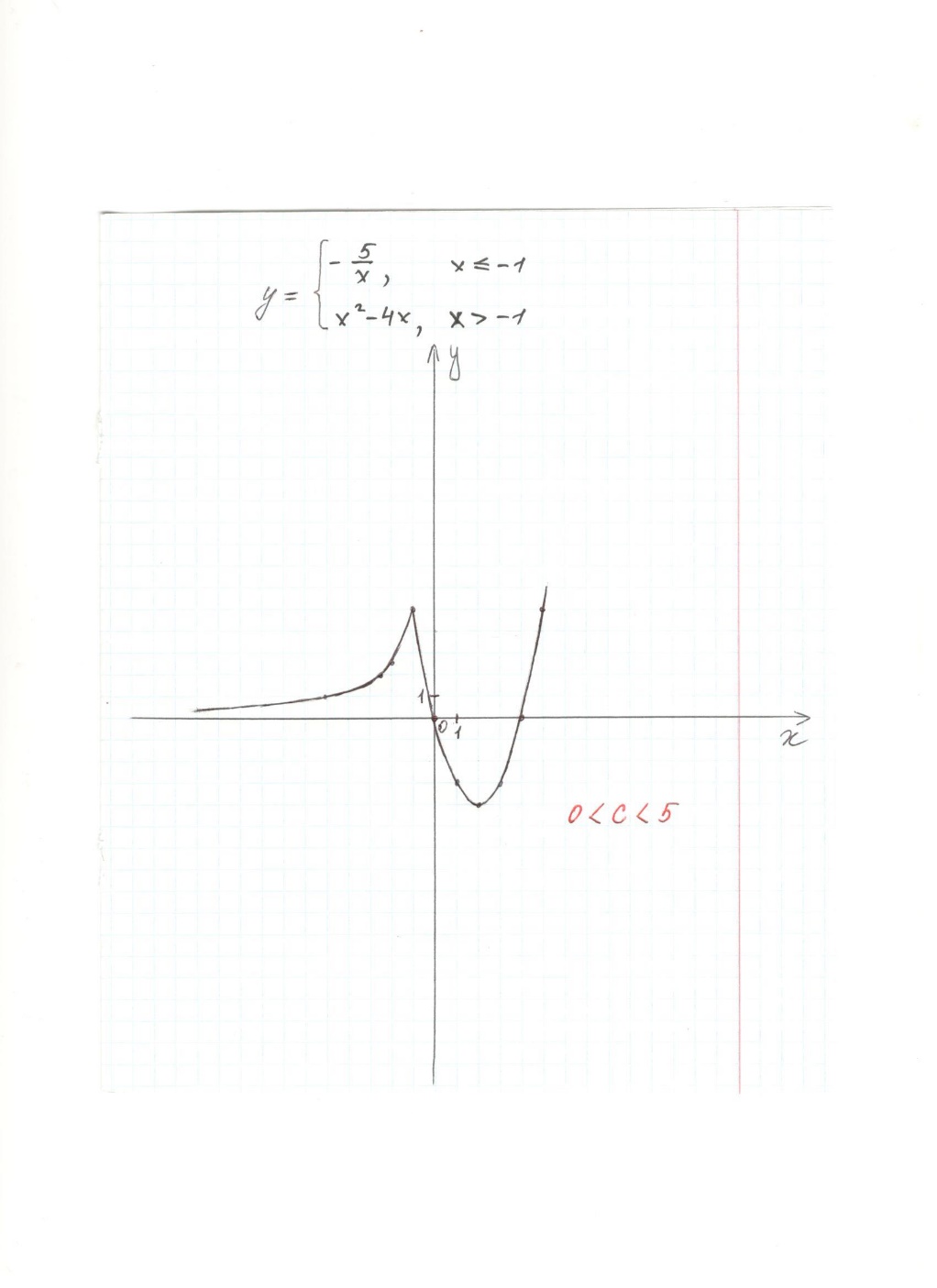
Рисунок 2. График функции y = 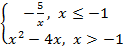(авторский)

Задание: при каких зна­че­ни­ях с пря­мая y=с имеет с гра­фи­ком 3 общие точки. При .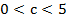

 

б) y =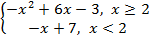     

1) Постройте график линейной функции y = 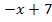 на промежутке

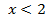
x	2	0
y	5	7

3) Постройте график квадратичной функции 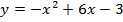 на промежутке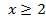

 =  =

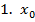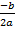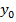 (3) = 6

   (3; 6) – вершина параболы

2. Ветви параболы вниз, т.к. a 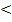0

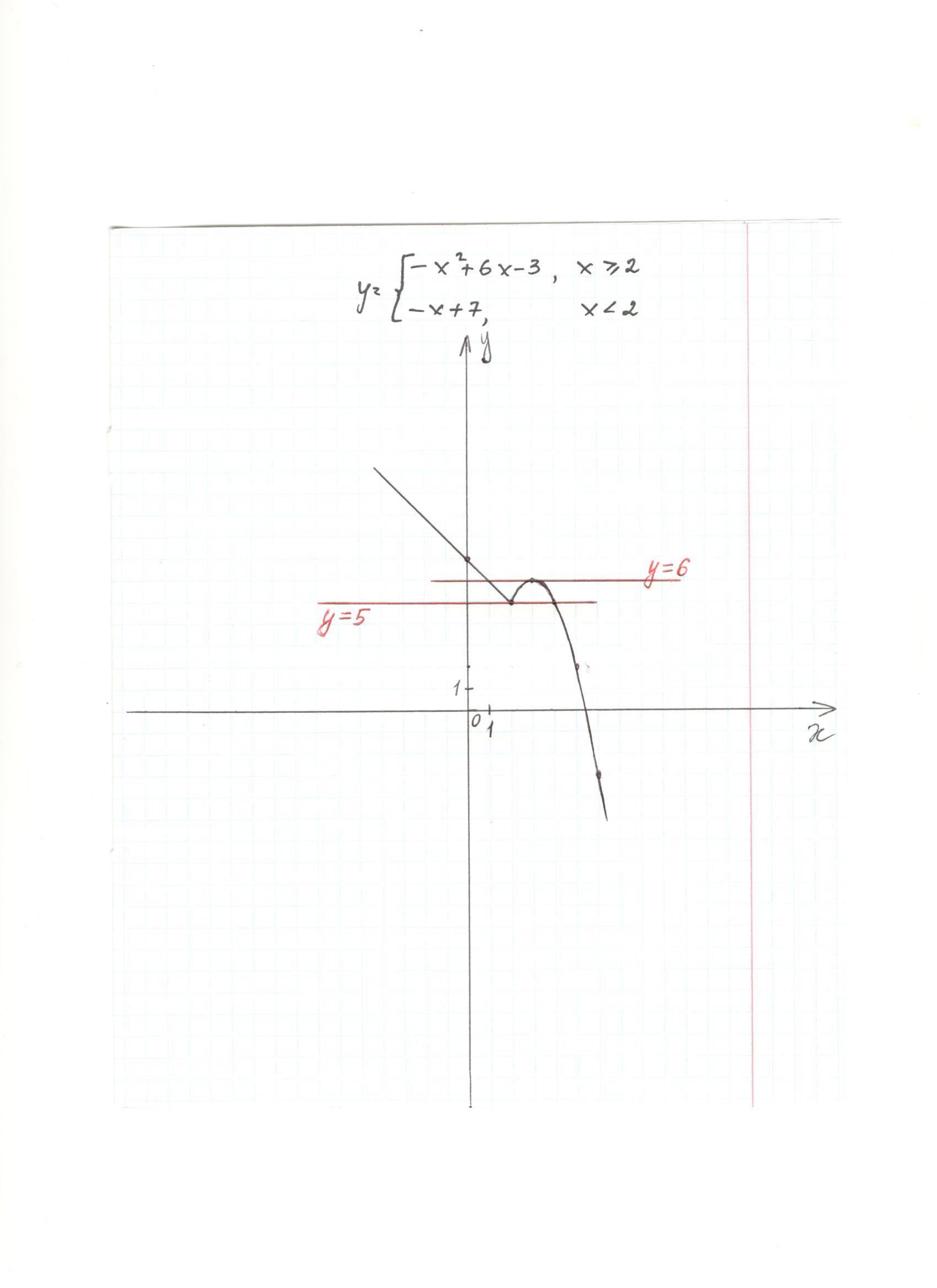
Рисунок 3. График функции y = 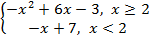(авторский)

Задание: при каких зна­че­ни­ях m пря­мая y=m имеет с гра­фи­ком две общие точки. При m= 6; 5.

Особенности построения графиков с модулями

Построение графика функции 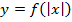, если известен график функции 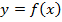. Для функции  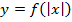можно записать:

Отсюда делаем вывод, что график функци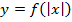и  при 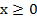 совпадает с графиком функции 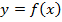, а при  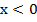– с графиком функции 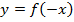. Тогда построение графика функции  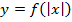можно проводить по такой схеме:

1) построить ту часть графика функции 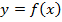, все точки которой имеют неотрицательные абсциссы;

2) построить ту часть графика функции 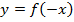, все точки которой имеют отрицательные абсциссы.

Объединение этих двух частей и составит график функции .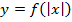

Построение графика функции 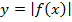, если известен график функции 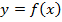. Для функции 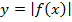можно записать:

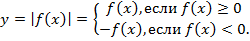
Отсюда следует, что график функции 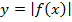 при всех х, для которых 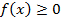, совпадает с графиком функции 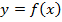, а при всех х, для которых 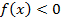, - с графиком функции .

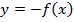Тогда строить график функции 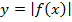 можно по такой схеме:

1) все точки графика функции 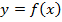 с неотрицательными ординатами оставить без изменений;

2) точки с отрицательными ординатами заменить на точки с теми же абсциссами, но с противоположными ординатами.