Построение графиков с модулем. Гипербола

y =

I. Раскройте знак модуля:

y =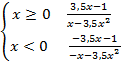   

II. Упростите:  =

III. Знаменатель не должен быть равен нулю:

0

x (1-3,5x)  0

x  0 или 1-3,5x  0

              x

IV. Постройте график обратной пропорциональности

x	4	2	1	0,5	0,25	-0,25	-0,5	-1	-2
y	-	-	-1	-2	-4	4	2	1

 

V. Упростите:  =

VI. Знаменатель не должен быть равен нулю:

0

-x (1+3,5x)  0

x  0 или 1+3,5x  0

              x

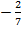
VII. Постройте график обратной пропорциональности

x	4	2	1	0,5	0,25	-0,25	-0,5	-1	-2
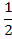
y			1	2	4	-4	-2	-1

 

Задание: при каких зна­че­ни­ях k пря­мая y=kx не имеет с гра­фи­ком общих точек. При k=-12,25; 12,25.

y = kx

(.) B ()

-3,5 = k *  

k = -3,5:  = -  *  = -  = -12,25

(.) A ()

-3,5 = k *  

k = -3,5:  = -  *-  =  = 12,25

 

Рисунок 4. График функции y =  (авторский)

Построение графиков с модулем. Парабола

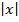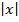а) y = x  + 2  – 5x

I. Раскройте знак модуля

II. Постройте график квадратичной функции y = 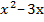 на промежутке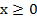

1. Найдите вершину параболы

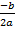 =  =  =  = 1,5

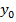 (1,5) = 1,5^2 – 3 * 1,5 = 2,25 – 4,5 = -2,25

   (1,5; -2,25) – вершина параболы

2. Ветви параболы вверх, т.к. a 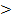0

3. Найдите координаты нескольких точек

y (0) = 0

III. Постройте график квадратичной функции y =  на промежутке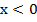

1.  =  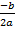=  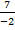=  = -3,5

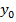 (-3,5) = - (-3,5)^2 – 7(-3,5) = 12,25

   (-3,5; 12,25) – вершина параболы

2. Ветви параболы вниз, т.к. a 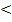0

     3. Найдите координаты нескольких точек

          y (0) = 0

Рисунок 5. График функции y = x 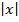 + 2 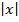 – 5x (авторский)

Задание: при каких зна­че­ни­ях m пря­мая y=m имеет с гра­фи­ком ровно две общие точки. При m=12,25; -2,25

б) y = x² -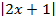

I. Найдите значения х, когда выражение 2х+1 меняет знак.

Нули: 2x+1=0

      2x=-1

      x=-0,5

II. Раскройте знак модуля

III. Постройте график функции y =  на промежутке

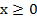
1. Найдите вершину параболы

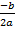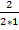 =  =  =  = 1

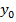 (2) = 1 – 2 – 1 = -2

   (1; -2) – вершина параболы

2. Ветви параболы вверх, т.к. a 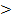0

3. Найдите координаты нескольких точек

y (0) = -1

y (3) = 9 – 6 – 1 = 2

IV. Постройте график функции y =  на промежутке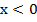

1.  =  =  =

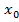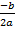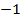
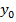 (-1) = 1 – 2 + 1 = 0

   (1; 0) – вершина параболы

2. Ветви параболы вниз, т.к. a 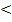0

     3. Найдите координаты нескольких точек

          y (0) = 1

Рисунок 6. График функции y = x² - 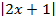 (авторский)

Задание: при каких зна­че­ни­ях m пря­мая y=m имеет с гра­фи­ком ровно три общие точки. При m=0,25; 0.

в) y =

I. Знаменатель не должен быть равен нулю:

x+2

x -2

II. Раскройте знак модуля: y =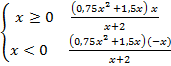   

 

III. Упростите выражение, раскрыв скобки, а затем вынеся общий множитель: y =  =  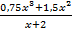=  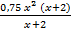= 0,75 =

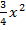
IV. Постройте график квадратичной функции 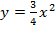 на промежутке

x	0	2	4
y	0	3	12

V. Упростите выражение, раскрыв скобки, а затем вынеся общий множитель:  =  = -0,75 =

VI. Постройте график квадратичной функции  на промежутке

x	0	-2	-4
y	0	-3	-12

Задание: при каких зна­че­ни­ях m пря­мая y=m не имеет с гра­фи­ком общих точек. При m= -3.

Рисунок 7. График функции y =  (авторский)