Условия равновесия системы сходящихся сил

На основании вышеизложенного можно сделать вывод, что для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю (). Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.

1. Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.

2. Аналитическое условие равновесия. . Так как под корнем стоит сумма положительных слагаемых, то выражение обратится в ноль только тогда, когда одновременно , ,    или   

                            , ,                                         (3)

Равенства (3) выражают условия равновесия в аналитической форме: для равновесия системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей были равны нулю.

    Из полученных условий равновесия можно получить следствие. Правило трех сил: если свободное твердое тело находится в равновесии под действием трех сил, лежащих в одной плоскости, две из которых пересекаются в одной точке, то линия действия третьей силы проходит через точку пересечения первых двух сил.  

13

Складываем две силы  и . Получаем равнодействующую этих сил 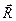. Тогда тело находится в равновесии под действием двух сил  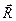и . А это возможно, только если эти силы прямопротивоположные (аксиома 1). Значит, линия действия силы  проходит через точку 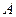 (рис. 14).

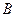
                                                   рис. 14