2020-05-12
146
Момент силы относительно оси равен проекции момента этой же силы, относительно точки лежащей на данной оси, на эту ось.
Рассмотрим силу,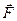 
расположенную в пространстве. Проводим плоскость 
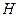, перпендикулярную оси 
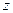и проходящую через точку приложения силы 
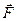. Определяем момент этой силы относительно точки 
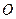, точки пересечения плоскости 
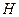и оси 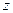. Из свойств момента силы относительно точки получаем, что модуль этого момента равен удвоенной площади треугольника 
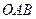, а направляется векторный момент перпендикулярно плоскости этого треугольника (рис. 19а).
Аналогично определяя момент силы 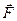относительно оси 
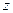получаем, что модуль этого момента равен удвоенной площади треугольника 
, а направляется векторный момент перпендикулярно плоскости этого треугольника (рис. 19б).
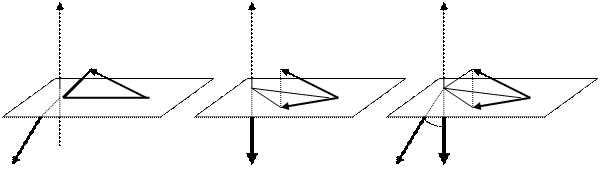
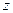
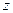
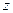
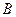
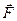
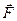
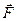
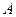
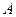
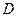
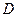
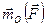
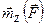
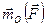
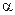
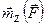
a) б) в)
рис. 19
В результате получаем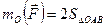 
, 
. С другой стороны, обозначая угол 
, между плоскостями треугольников 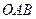и , через 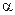получаем, что 
. Тогда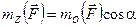 
. Если мы посмотрим на рисунок 19в, то из векторов моментов можно получить следующее равенство 
. (5)
Зависимость (5) устанавливает связь между моментами силы относительно центра и относительно оси, которую мы записали словами в начале параграфа.
