2020-05-12
288
Теорема о сложении пар, лежащих в одной плоскости. Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющий момент равный алгебраической сумме моментов слагаемых пар.
Доказательство: Пусть на тело действуют три пары с моментами 
, 
, 
(рис. 24а). На основании теоремы об эквивалентности пар мы можем заменить эти пары тремя парами 
, 
, 
, имеющими общее плечо 
и такие же моменты: 
, 
, 
(рис. 24б). Складывая отдельно силы, приложенные в точках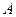 
и 
, получаем в точке силу 
, а в точке 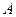силу 
, которые по модулю будут равны 
(рис. 24в).
В результате вся система пар заменяется одной парой 
с моментом 
. Для случая из «n» пар с моментами , , … 
, система заменяется одной парой с моментом 
. Если пары расположены в пространстве, то можно перейти к векторному равенству 
. Проектируя это векторное равенство на оси декартовой системы координат, получаем: 
, 
, 
.
Отсюда получаем условие равновесие произвольной системы пар: для равновесия произвольной системы пар необходимо и достаточно, чтобы момент результирующей пары был равен нулю 
.
21
Геометрическое условие равновесия:для равновесия произвольной системы пар необходимо и достаточно, чтобы векторный момент результирующей пары был равен нулю .
Аналитическое условие равновесия: 
или через проекции на оси 
, 
, 
. (6)
