Практическое занятие №6

1 Наименование работы: Функция распределения и плотность распределения НСВ. Вычисление характеристик НСВ.

2 Цель работы: отработать навык решения задач.

Формирование ОК 1, 3-5,8; овладение знаниями и умениями, необходимыми для освоения ПК 1.1, 1.2. (спец. 09.02.03.), ПК 1.2, 1.4. (спец. 09.02.04.).

3 Подготовка к занятию: Повторите тему: «Характеристики НСВ».

4 Литература:

4.1 Учебное пособие по дисциплине «Теория вероятностей и математическая статистика», 2018.

4.2 Приложение к ПЗ №6.

5 Перечень необходимого оборудования и материалов:

5.1 Бланк для отчета.

5.2 Канцелярские принадлежности.

6 Задание на занятие:

1. F(x)=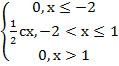

Найти:

1)c

2)M(x),D(x),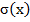

2.  f(x)=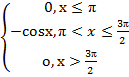

Найти:

1)M(x),D(x),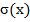

3.   f(x)=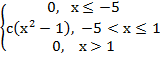

Найти:

1)с

2)F(x)

 

7 Порядок выполнения работы:

Выполните практическую работу в соответствии с заданиями (основная часть п.п. 6.1 – 6.3) и сдайте зачет).

8 Содержание отчета:

Решения задач в соответствии с заданием.

 

9 Контрольные вопросы:

1. Какую величину называют непрерывной?

2. Плотность распределения вероятностей и ее гафик.

3. Числовые характеристики НСВ.

 

ПРИЛОЖЕНИЕ:

       Непрерывной называют величину, все возможные значения которой полностью заполняют конечный или бесконечный промежуток числовой оси.

      Функцией распределения непрерывной случайной величины Х называется функция F(х), определяющая для каждого значения   х 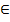R

 вероятность того, что случайная величины Х в результате испытания примет значение, меньшее х: F(x)=P(X<x),где х 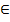R

Плотностью распределения вероятностей f(x) непрерывной случайной величины Х называется производная от ее функции распределения, т.е.:

f(x)=F’(x)

       Графикплотности распределения вероятностей f(x) называется кривой распределения вероятностей.

 Пример 1. Случайная величина Х задана плотностью распределения вероятностей:

     0     при х≤2,

f(x)= с(х-2) при 2<х≤6,

     0     при х>6.

  Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в) Р(3≤х<5)

 _{+∞             2         6}                    +∞   6                             ₆

 ∫ f(x)dx=∫ 0dx+ ∫ c(х-2)dx +∫ 0dx= c∫ (х-2)dx=с(х²/2-2х) =с(36/2-12-(4/2-4))=8с;

 ^{-∞            -∞        2                      6             2                                            2}    

8с=1;

с=1/8.                              _х

б) Известно, что F(x)= ∫ f(x)dx

                                      ^-∞

 

 Поэтому,             _х

если х≤2, то F(x)= ∫ 0dx=0;

                                          ^-∞   _{2         2                                                     х}

если 2<х≤6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx=1/8(х²/2-2х) = 1/8(х²/2-2х- (4/2-4))=

                                                     ^{-∞      -∞                                                     2}

=1/8(х²/2-2х+2)=1/16(х-2)²;

                                             _{2         6                          х                  6                                              6}

если х>6, то F(x)= ∫ 0dx+∫ 1/8(х-2)dx+∫ 0dx=1/8∫(х-2)dx=1/8(х²/2-2х) =

                                           ^{-∞         6                  2                      2                             2}

=1/8(36/2-12-(4/2+4))=1/8•8=1.

Таким образом,

        

 

        0         при х≤2,

F(х)= (х-2)²/16 при 2<х≤6,

 1       при х>6.

 

График функции F(х) изображен на рис.

 

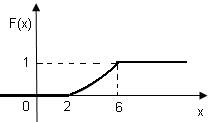
в) Р(3≤Х<5)=F(5)-F(3)=(5-2)²/16-(3-2)²/16=9/16-1/16=5/16.

Пример 2. Случайная величина Х задана функцией распределения:

         0            при х≤0,

F(х)= (3• arctg х)/π при 0<х≤√3,

         1             при х>√3.

 

Найти дифференциальную функцию распределения f(х)   

 

Решение: Т.к.f(х)= F’(x), то   

         0             при х≤0,

f(х)= (3•(1+х²)) /π при 0<х≤√3,

         0              при х>√3.

 

Математическое ожидание М (Х) непрерывной случайной величины Х определяются равенством:

                                                      _+∞

M(X)= ∫ x•f(x)dx,

                                                 ^-∞

при условии, что этот интеграл сходится абсолютно.

Дисперсия D(X) непрерывной случайной величины Х определяется равенством:

                                                                      _+∞

D(X)= ∫ (х-М(х)²)•f(x)dx, или

                                                                             ^-∞

                                                                                                _+∞

D(X)= ∫ х²•f(x)dx- (М(х))²

                                                                                              ^-∞

Среднее квадратическое отклонение σ(Х) непрерывной случайной величины определяется равенством: