Маршруты, цепи и циклы

Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретают направление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь (простая цепь) в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).

Контур (простой цикл) – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

Пример 4:

Пример незамкнутого маршрута:

Пример замкнутого маршрута:

Пример цепи:

Пример пути (простой цепи):

Пример цикла:

Пример контура (простого цикла):

Метрические характеристики графа.

Расстоянием между вершинами и называется длина кратчайшего маршрута соединяющего эти вершины и обозначается .

Эксцентриситетом вершины  называется величина, которая равна расстоянию от данной вершины до наиболее отдаленной от нее и обозначается .

Диаметром графа называется максимальный из всех эксцентриситетов графа и обозначается .

Вершина  называется периферийной, если .

Радиусом графа называется минимальный из всех эксцентриситетов вершин и обозначается .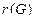

Вершина  называется центральной, если . Множество всех центральных вершин называется центром графа.