2020-05-12
242
Число ребер графа G, инцидентных данной вершине 
называется степенью (валентностью) данной вершины и обозначается 
.
Вершина называется изолированной, если ее степень равна нулю.
Вершина называется висячей, если ее степень равна единице.
Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой.
Полустепенью исхода (захода) вершины оргафа называется число 
(
) его дуг, исходящих из вершины 
(заходящих в вершину 
)
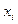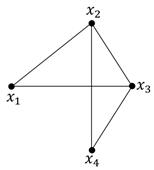Пример 2:
Способы задания графа.
1. Перечислением вершин и ребер.
2. Графическим способом с помощью диаграммы.
Матричным способом.
1) Матрицей смежности вершин графа G=(S,U) порядка n называется квадратная матрица порядка n, строки и столбцы которой соответствуют вершинам графа, где элементы 
равны числу дуг, идущих из i-ой вершины, в j-ую.
2) Матрицей смежности дуг графа G=(S,U),где 
, называется квадратная матрица, порядка m, элементы которой 
равны единице, если дуга 
непосредственно предшествует дуге 
, и равны нулю в остальных случаях.
3) Матрица инцидентности -одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам.
Пример 3:
Для данного графа построить матрицы смежности вершин и дуг.
