Цепи с распределенными параметрами

Устройство и назначении линий передачи. Передача сигналов от генератора к нагрузке выполняется при помощи системы проводников, которые обычно называют линиями передач. Устройство линий передач может быть различным и зависит от их назначения, области применения, диапазона частот и других факторов. По конструкции линии передачи разделяют на следующие группы: двухпроводные, коаксиальные, полосковые, многопроводные.

Линия передачи называется длинной, если ее длина соизмерима с длиной волны, которая по ней распространяется. Основным назначением линии передачи является передача электромагнитной энергии от одного устройства к другому. Однако, кроме этого длинные линии находят применение в качестве резонансных колебательных систем, излучающих устройств, трансформаторов сопротивлений и некоторых других устройств. Особенностью линии передачи является невозможность разграничения в ней элементов, содержащих магнитную. электрическую или тепловую энергию.

Первичные параметры линии. Схематическое изображение линии передачи приведено на рисунке 4.1, а. На этом рисунке линия передачи представлена в вид двух проводов, к которым с одной стороны подключен источник напряжения и₁ а с другой - нагрузка z₂. Общая длина линии равна l, а отсчет координаты рассматриваемого сечения линии ведется или от источника напряжения (расстояние х) или от нагрузки (расстояние у), при этом выполняется условие у = 1 - х.

Каждый бесконечно малый участок длинной линии несет в себе все перечис­ленные выше виды энергии и может быть замещен эквивалентной Г-образной схемой, приведенной на рисунке 4.1, б. В последовательном плече этой схемы включены элементарные бесконечно малые сопротивление dR и индуктивность dL. Аналогично, в параллельном плече включены элементарная проводимость dG и емкость dC.

Отношение этих величин к элементу’ длины линии dx = ~dy называют погонными параметрами линии.. Eсли линия однородна по всей длине, то ее погонные параметры постоянны и определяются по формулам:

              (4.1)

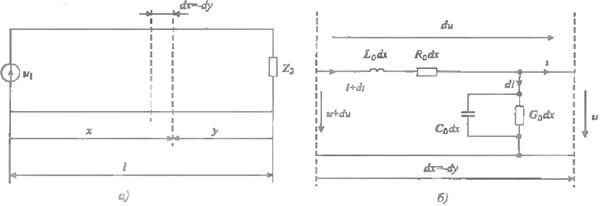Рисунок 4.1.Линия передачи а) и схема замещения се участка

длиной dx (б.

Эти погонные параметры, представляющие собой значения сопротивления. индуктивности, проводимости и емкости, приходящиеся на единицу длины линии, называются первичными параметрами линии.

Погонное сопротивление линии R₀ учитывает потери в двух проводах линии передачи. Это сопротивление растет с ростом частоты, что обусловлено поверхностным эффектом. Аналогично, погонная индуктивность L₀ учитывает результирующую индуктивность двух проводников на единицу длины линии. С увеличением диаметра проводников индуктивность уменьшается.

Погонная емкость линии С₀ характеризует емкость между ее проводниками на единицу длины. Эта емкость растет с увеличением диаметра проводников и уменьшением расстояния между ними. Она также зависит от диэлектрической проницаемости изоляции между проводниками. Погонная проводимость G_t учитывает потери в изоляции между проводниками линии. С ростом частоты погонная проводимость увеличивается, так как растут потери в изоляции. В воздушных линиях передачи погонную проводимость не учитывают ввиду ее малости Значения погонных параметров для двух типов воздушных линий (двухпроводной и коаксиальной) из медныx проводников приведены в таблице 4.1.

Таблица 4.1

Погонные параметры воздушных линий передачи

Тип линии	R0, мкОм/м	G0, мкСм/м	L0, мкГн/м	Со, пФ/м
Двухпроводная		G+ kf	0,41n (2 a/d)	28/ln(2a/d)
Коаксиальная			0,2 In (d1/d2)	55In (d2/d1)

где: f - частота тока в Гц, d - диаметр проводника в см, G. - проводимость изоляции на постоянном токе в См/м, 8 - угол диэлектрических потерь, а - расстояние между проводниками.

Дифференциальные уравнения линии передачи. Уравнения линии могут быть получены из рассмотрения модели, приведенной на рис 4.1. При рассмотрении процессов, происходящих в Линии, будем считать, что напряжение и ток в линии являются функциями двух переменных - времени г и пространственной координаты х (или у).

Используя погонные параметры линии передачи (4.1), получим:

Уравнения линии, определяющие приращения напряжения и тока на участке линии длиной dx, можно записать в виде:

в которых используются частные производные 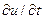 и , так как ток i(x, t) и напряжение и(х, t) являются функциями двух переменных х и t.

Учитывая, что  и  из (4.2) получаем:

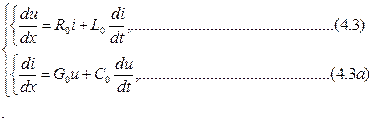
В уравнениях линии (4.3) можно разделить переменные. Для этого следует уравнение (4.3) продифференцировать по t, а уравнение (4.3 а) - по х, тогда получим:

Произведя подстановку уравнения (4.4) в уравнение (4.4 а), получим дифференциальное уравнение для тока в линии:

                (4.5)

Аналогично можно получить дифференциальное уравнение для напряжения в линии:

                (4.5a)

Уравнения (4.5) и (4.5 а) называют телеграфными уравнениями и их сравнение показывает, что решения для тока и напряжения следует искать в одной и тон же форме В общем случае эти уравнения можно решить только при известных граничных условиях, в качестве которых обычно используют напряжения и токи в конце или начале линии. Полные интегралы этих уравнений позволяют определить токи и напряжения в линии как в стационарном, так и в переходном режимах.

Уравнения линии в стационарном режиме при гармоническом сигнале. При гармоническом напряжении  и токе 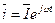, выполнив дифференцирование по времени и подставив полученные значения в уравнения (4.5) и (4.5а), получим для комплексных значений напряжения и тока дифференциальные уравнения в полных производных:

                (4.6)

                    (4.6a)

где  и  - погонные комплексные сопротивление и проводимость линии, соответственно.

Характеристическое уравнение для дифференциальных уравнений (4.6) и (4.6а) имеет одинаковый вид:

                                                (4.7)

а его решение дает два корня , где  - коэффици­ент распространения волны в линии.

Решение уравнения (4.6) ищется в виде:

                                             (4.8)

где А и В - постоянные интегрирования, определяемые из граничных условий. Аналогичное решение имеет уравнение (4.6а)

                                           (4.8a)

где С и D - постоянные интегрирования, также определяемые из граничных условий.

Поскольку нз уравнения (4.3) следует, что:

то, выполняя дифференцирование уравнения (4.8), найдем постоянные интег­рирования 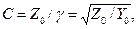, поэтому уравнение (4.8а) можно записать в виде:

                                       (4.9)

где  - характеристическое (волновое) сопротивленце читт передачи.

Из уравнений (4.8) и (4.9) следует, что напряжение  и ток  состоят из двух составляющих. Первые составляющие в этих уравнениях характеризу­ют падающие волны напряжения и тока, которые перемещаются от источника к нагрузке, вторые - отраженные волны, которые перемещаются в обратном направлении. В связи с этим уравнения (4.8) и (4.9) можно представить в виде суммы падающих и отраженных волн напряжения и тока:

                                  (4.10)

                                    (4.10a)

где  -   напряжение падающей волны;

 - напряжение отраженной волны,

 - ток падающей волны;

 - ток отраженной волны.

Напряжения и токи падающих и отраженных волн связаны законом Ома:

                                       (4.11)

В зависимости от заданных граничных условий значения постоянных интегрирования А и В могут выражаться различным образом:

- через напряжение 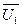, и ток , в начале линии (т. е. при х = 0),

- через напряжение , и ток 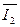, в начале линии (т. е. при y = 0),

- через напряжение 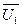, и и сопротивление нагрузки  и т.д.

Кроме этого, уравнения линии можно представить в гиперболических функциях, используя известные соотношения:

Различные формы записи уравнений линии приведены в таблице 4.2. В этих уравнениях учтено введенное ранее условие у = 1 - х и использовано соотношение .

Вторичные параметры линии. Вторичными параметрами линии являются ее волновое сопротивление и коэффициент распространения волн тока и напряжения.

Волновое сопротивление Z_С можно рассматривать как входное сопротивление бесконечно длинной однородной линии и определять через первичные параметры по формуле:

                                   (4.12)

В общем случае волновое сопротивление линии является комплексным и может быть представлено в виде:

                                   (4.13)

где  -  модуль волнового сопротивления;

 - аргумент волнового сопротивления;

r_C и х_C, - соответственно активная и реактивная составляющие волнового

сопротивления.

Таблица 4.2

Уравнения линии передачи

На постоянном токе (ω = 0) и очень высокой частоте (ω→∞) волновое сопротивление вещественное:

                        (4.14)

Если потери в линии малы (R₀ ˂˂ ωL₀, G₀ ˂˂ C₀), то волновое сопротивление имеет емкостной характер:

                        (4.15)

Для кабельных линий при выполнении условий  активная и реактивная составляющие волнового сопротивления оказываются одинаковыми:

                                    (4.16)

Процесс распространения вдоль линии волн напряжения или тока характе­ризуется коэффициентом распространения:

                                    (4.17)

В общем случае коэффициент распространения представляет собой комплексную величину γ = а + jp, в которой вещественная часть а характеризует эатухание амплитуды волн на единичном отрезке длины линии, а мнимая часть β характеризует изменение фазы волны на том же отрезке линии.

Коэффициент затухания измеряется в нсперах или белах на метр, а коэффициент фазы - в радианах или градусах на метр. Произведение коэффициента затухания на длину отрезка линии определяет затухание волны в данном отрезке.

 или

где U₁ и U₂ - напряжение в начале и конце отрезка линии.

Так как непер и бел являются сравнительно крупными единицами, то на практике большое распространение получила единица затухания, называемая децибелом (дБ) и определяемая как 0,1 Б, причем:

                                         (4.18)

Затухание волн тока определяется аналогично затуханию волн напряжения:

=

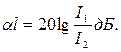
где I₁, и 1₂ - токи соответственно в начале и конце линии.

В ряде случаев затухание определяют через мощности Р₁ в начале отрезка линии и Р₂ в конце отрезка линии. При этом расчет затухания производится по формуле:

=

При переходе от одних единиц измерения затухания к другим можно пользоваться соотношением 1 Нп = 0,8686 дБ.

При расчете коэффициентов затухания и фазы по первичным параметрам линии можно пользоваться выражениями:

      (4.19)

      (4.19a)

Если потери в линии достаточно малы, то расчет коэффициентов затухания и фазы можно производить по упрощенным формулам:

 при R₀ ˂˂ ωL₀ и G₀ ˂˂ ωC₀

Для линии без потерь (R₀ = G₀ =0) справедливы соотношения

                             (4.20)

Если линия работает на постоянном токе (ω = 0), то β = 0, а  Для кабельной линии обычно выполняется условие G₀ = L₀ = 0. При этом расчет коэффициентов затухания и фазы производится по формуле:

Коэффициент отражения. Коэффициентом отражения волны в линии называется отношение комплекса отраженной волны к комплексу падающей волны напряжения или тока:

                             (4.21)

Отражение в неоднородны линиях возникает в месте нарушения однородности (например, в месте соединения двух линий с различными волновыми сопротивлениями). В однородных линиях отражение возникает в местах подключения генератора или нагрузки Отражение от генератора характеризуется коэффициентом отражения от начала линии (x = 0):

                             (4.22)

где  - входное сопротивление линии.

Отражение от нагрузки характеризуется коэффициентом отражения от конца линии:

                     (4.23)

где  - сопротивление нагрузки.

Для линии, согласованной с нагрузкой и генератором (Z₁ = Z₂ =- Z_С) коэффициенты отражения  Если линия закорочена или разомкнута на конце (Z₂ = 0 или Z₂ = ∞), то в ней возникает полное внутреннее отражение и | Г | = 1.

Входное сопротивление. Входное сопротивление линии равно отношению напряжения к току на входе линии:

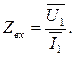                                               (4.24)

Входное сопротивление позволяет заменить рассмотрение цепей с распределенными параметрами цепями с сосредоточенными параметрами. При анализе линий с потерями входное сопротивление можно определить по формуле:

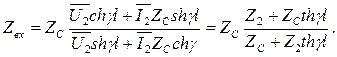               (4.25)

Если линия    согласована с нагрузкой (Z₂ = Z_c)_s то Z_вх    = Z_c Для линии, закороченной на конце (Z₂ =    0):

                                           (4.26)

Для линии, разомкнутой на конце (Z₂ = ∞):

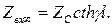                                           (4.26a)

Входное сопротивление линии можно определять по режимам холостого хода и короткого замыкания:

                                    (4.27)

Включение нагрузки в линию можно рассматривать как изменение се дли­ны. При этом входное сопротивление определяется выражением:

                                           (4.28)

где 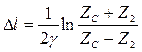 - эффективное удлинение линии.

Эффективное удлинение Δl → ∞ для линии, согласованной с нагрузкой (Z₂ = Z_c). Для закороченной на конце линии Δl =     0.

Значения входного сопротивления линии в режимах короткого замыкания и холостого хода позволяют определить вторичные параметры:

                                           (4.29)

                                           (4.30)

                                           (4.31)

Фазовая скорость волны в линии. Волны напряжения и тока распространяются в линии с конечной скоростью. Фазовая скорость волны определяется скоростью, с которой распространяется вдоль линии любое значение бегущей волны тока или напряжения с фиксированной фазой:

                                           (4.32)

Кроме фазовой скорости, волна в линии характеризуется еще своей длиной λ представляющей кратчайшее расстояние между двумя точками линии, в которых фаза    колебания волны в любой момент одинакова. Это означает, что фазовые углы в точках х и х + λ отличаются на 2π,   откуда следует, что:

                                           (4.33)

Зависимость фазовой скорости от частоты колебания приводит к искаже­нию формы сложного сигнала, распространяющегося в линии. Такое явление получило название дисперсии волны в липни. Дисперсия волны в линии отсутствует, если коэффициент фазы пропорционален частоте колебаний:

Линия без искажений. Линия не искажает передаваемого по ней сложного сигнала, если коэффициент затухания и фазовая скорость волны в ней на всех частотах одинаковы. Такое положение имеет место в том случае, когда выполняется условие:

                                    (4.34)

В этом случае коэффициент затухания не зависит от частоты:

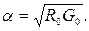                                    (4.35)

а коэффициент фазы пропорционален частоте:

                                    (4.35)

Фазовая скорость в линии без искажений постоянна:

                                           (4.37)