Рассмотрис метод моделирования случайной величины, которая имеет функцию плотности распределения 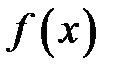 и монотонно возрастающую функцию распределения
и монотонно возрастающую функцию распределения 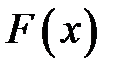 . Суть метода заключается в следующем. С помощью генератора случайных чисел генерируем значение случайной величины
. Суть метода заключается в следующем. С помощью генератора случайных чисел генерируем значение случайной величины  , которому соответствует точка на оси ординат. Значение случайной величины
, которому соответствует точка на оси ординат. Значение случайной величины 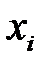 с функцией распределения
с функцией распределения 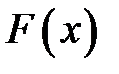 можем получить из уравнения
можем получить из уравнения 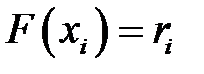 .
.
Действительно, если на оси ординат отметить значение  случайной величины, распределенной равномерно в промежутке
случайной величины, распределенной равномерно в промежутке 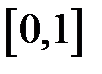 , и на оси абсцисс найти значение
, и на оси абсцисс найти значение 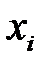 случайной величины (рис. 1), при котором
случайной величины (рис. 1), при котором 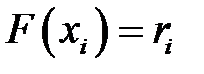 , то случайная величина
, то случайная величина  будет иметь функцию распределения
будет иметь функцию распределения 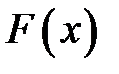 . По определению функция распределения
. По определению функция распределения 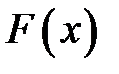 случайной величини
случайной величини 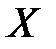 равна вероятности
равна вероятности 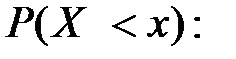
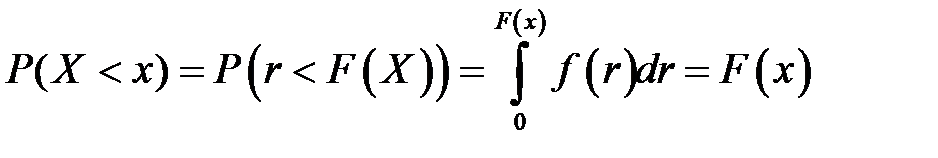
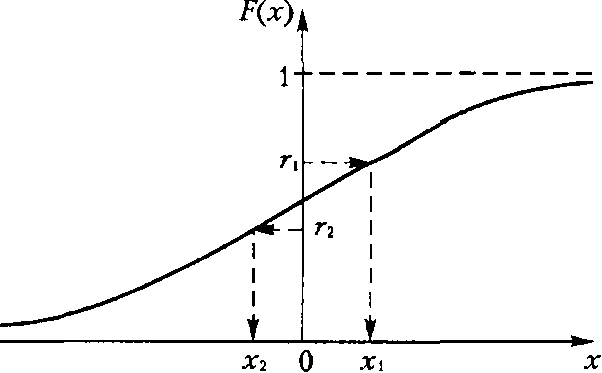
Рис. 1. Применение метода обратной функции
для генерирования непрерывной случайной величины
Таким образом, последовательность случайных чисел 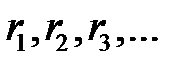 превращается в последовательность
превращается в последовательность 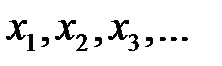 , которая имеет заданную функцию плотности распределения
, которая имеет заданную функцию плотности распределения 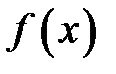 . Откуда следует общий алгоритм моделирования непрерывных случайных величин, имеющих заданную функцию распределения вероятностей:
. Откуда следует общий алгоритм моделирования непрерывных случайных величин, имеющих заданную функцию распределения вероятностей:
- генерируются случайные числа 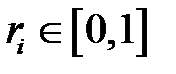 ;
;
- вычисляется случайное число 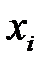 , которое является решением уравнения:
, которое является решением уравнения:
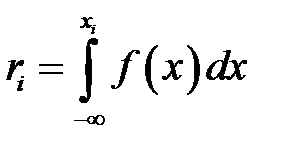
 2020-05-13
2020-05-13 322
322








