2020-05-13
187
В общем случае случайная величина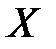 
является равномерно распределенной на прожутке 
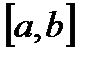, если её плотность распределения вероятностей имеет вид:
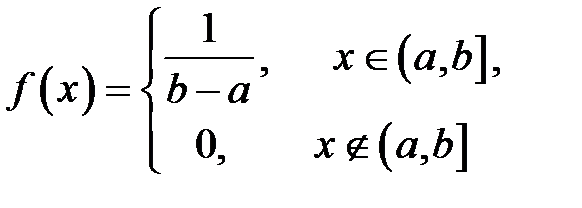
Функцию распределения вероятностей можно найти как
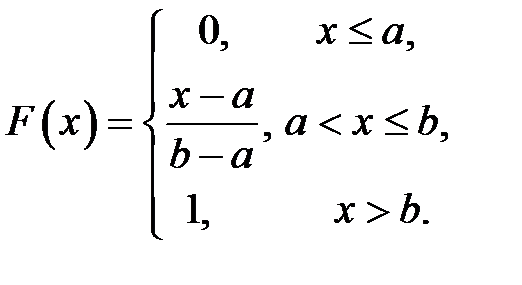
Графики функций плотности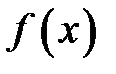 
и распределения вероятностей 
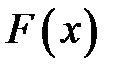показаны на рис.2.
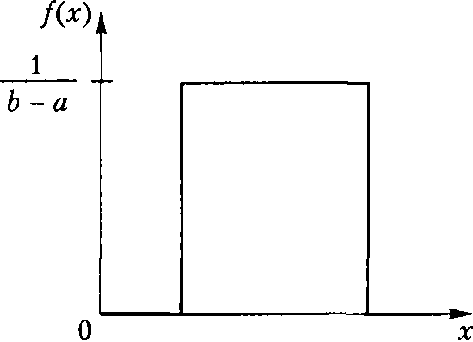
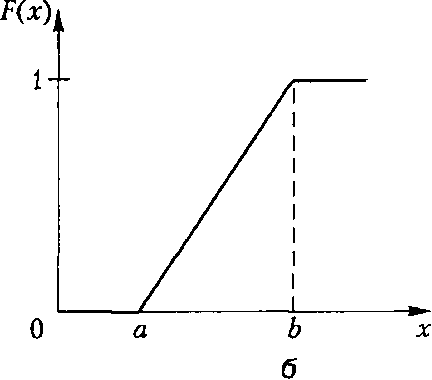
(а) (б)
Рис. 2. Функции плотности (а) и распределения(б) равномерно распределенной случайной величины
Числовые характеристики случайной величины 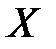определяются как
, 
, 
, 
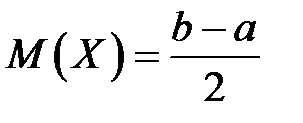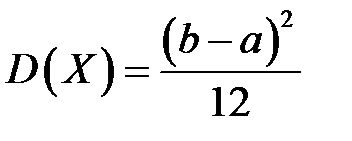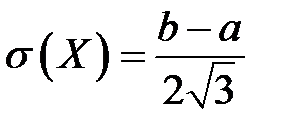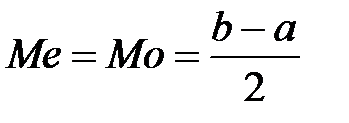
Для моделирования случайной равномерно распределенной величины на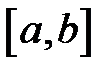 
можно воспользоваться методом обратной функции. Вычислим функцию распределения случайной величины и приравняем её к значению 
:
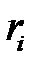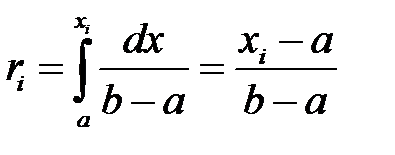
Откуда находим значение случайной величины с функцией распределения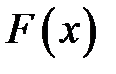 
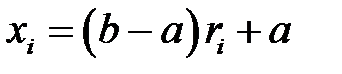
Функция равномерного распределения широко применяется для моделирования случайных величин, для которых функция распределения неизвестна, а известно лишь её среднее значение. В языке 
такое распределение часто используется в блоках 
для моделирования задержки прохождения информации или при генерировании потоков транзитов в блоках 
.
Примерами реальних задач, в которых возникает необходимость моделирования равномерно распределенных случайных величин, могут быть анализ ошибок округления при проведении числовых расчетов, время перемещения головки в магнитных накопителях, отклонение от расписания движения транспортных средств.
