с нормальным законом распределения.
Случайная величина 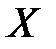 имеет нормальный закон распределения вероятностей, если
имеет нормальный закон распределения вероятностей, если
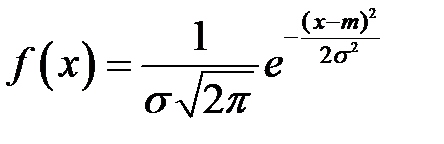 ,
, 
 ,
,
где  ,
,  . Следовательно, нормальный закон определяется параметрами
. Следовательно, нормальный закон определяется параметрами 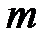 и
и  и называется общим.
и называется общим.
Тогда функция распределения нормально распределенной величины 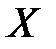
F (x) = 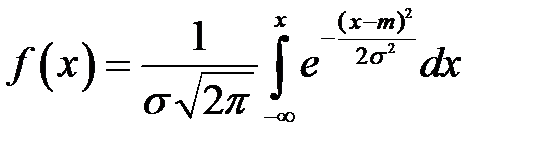 .
.
Если 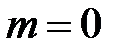 и
и 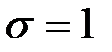 , то нормальный закон называют нормированным. В этом случае
, то нормальный закон называют нормированным. В этом случае
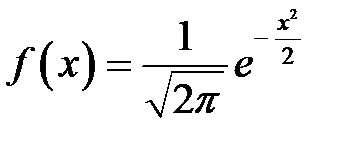 ,
, 
 ,
,
т.е. 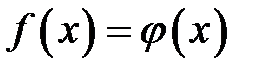 является функцией Гаусса,
является функцией Гаусса,
 .
.
Графики f (x), F (x) для общего нормального закона в зависимости от параметров а и s изображены на рисунках 3 и 4.
Рис. 3 Рис. 4
Для моделирования случайной величины с нормальным законом распределения непосредственно воспользоваться методом обратной функции нельзя, т.к. невозможно аналитически выполнить преобразования вида  . Поэтому для моделирования следует использовать метод свёрток.
. Поэтому для моделирования следует использовать метод свёрток.
Метод свёрток базируется на центральной граничной теореме – одном из наиболее выдающихся результатов теории вероятностей (при широких допущениях относительно распределений суммы большого количества взаимно независимых малых случайных величин имеет место распределение, которое является близким к нормальному распределению). Метод свёрток предусматривает изображение случайной величины в виде суммы независимых одинаково распределенных случайных величин с конечным математическим ожиданием и дисперсией.
Центральная граничная теорема формулируется так.
Если 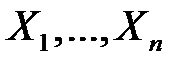 – последовательность независимых случайных величин с конечным математическим ожиданием
– последовательность независимых случайных величин с конечным математическим ожиданием 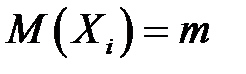 ,
, 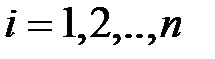 , и дисперсией
, и дисперсией 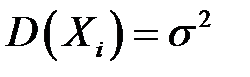 ,
, 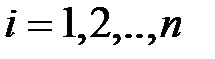 , то в случае неограниченного увеличения значения
, то в случае неограниченного увеличения значения 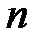 функция распределения случайной величины
функция распределения случайной величины
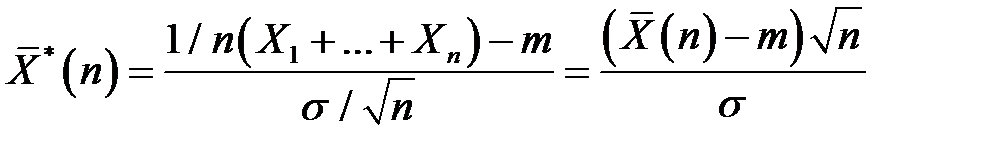
Приближается к функции распределения стандартного нормального закона Ф (і) при всех значениях аргумента, т.е.
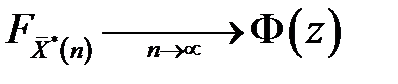
где
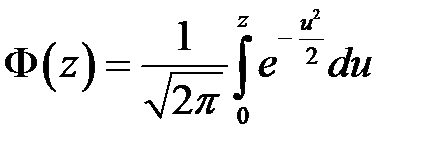 ,
, 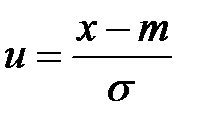 .
.
 – функция Лапласа.
– функция Лапласа.
Простейший метод получения значения случайной величины, имеющей заданное нормальное распределение, предусматривает выполнение таких шагов.
Сначала формируют последовательность 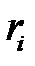 ,
, 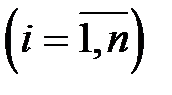 независимых, равномерно распределенных на
независимых, равномерно распределенных на 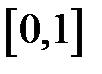 величин и вычисляют сумму
величин и вычисляют сумму 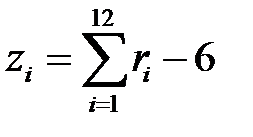 . Величина
. Величина 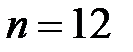 является хорошим приближением к нормальному распределению случайной величины с нулевым математическим ожиданием
является хорошим приближением к нормальному распределению случайной величины с нулевым математическим ожиданием 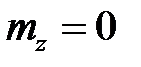 и единичным средним квадратическим отклонением
и единичным средним квадратическим отклонением 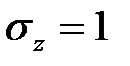 . Такое распределение называется стандартным. Перейти от случайной величины
. Такое распределение называется стандартным. Перейти от случайной величины 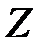 с
с 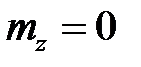 и
и 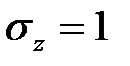 к случайной величине
к случайной величине 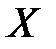 , которая имеет математическое ожидание
, которая имеет математическое ожидание 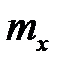 и среднее квадратическое отклонение
и среднее квадратическое отклонение 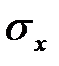 , даёт возможность линейное превращение:
, даёт возможность линейное превращение: 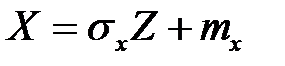 .
.
 2020-05-13
2020-05-13 121
121








