Моделирование непрерывной случайной величины

С логарифмически-нормальным законом распределения

Логарифмически-нормальное распределение – это такое распределение случайной величины, в которой нормальное распределение имеет натуральный логарифм её значений. Это распределение применимо для моделирования мультипликативных процессов так же, как и нормальное распределение – для аддитивных процессов. Можно показать, что произведение независимых положительных случайных величин стремится к логарифмически-нормальному распределению.

Случайная величина 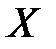 имеет логарифмически-нормальный закон распределения вероятностей, если

, ,

где , .

Значения случайной величины х с логарифмически-нормальным распределением всегда положительные и используются при моделировании экономических, физических, биологических систем многих типов.

Случайными величинами с этим распределением являются, в частности, размер банковского вклада, длина слов определенного языка и переданных сообщений в сети, размеры файлов, которые хранятся в компьютере.

Метод моделирования логарифмически-нормального распределения предусматривает подстановку в уравнение   значений из выборки , которые имеют нормальное распределение с математическим ожиданием m и дисперсией σ ², где L — логарифмически-нормальное распределение. Характеристики этого распределения:

,                                         .