2020-05-13
164
Случайная величина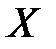 
имеет гамма-распределение с параметрами α (параметр формы распределения) и β (масштабный коэффициент), если его плотность описывается выражением:
, 
.
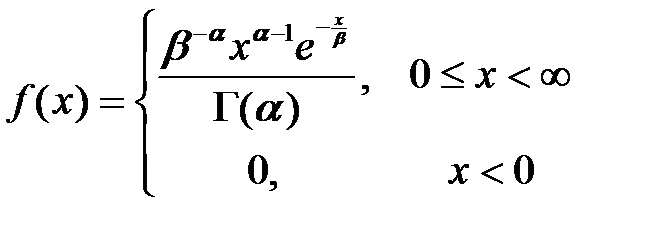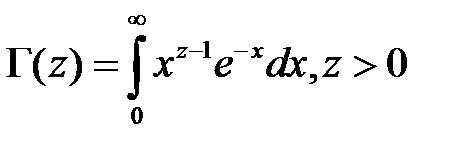Математическое ожидание и дисперсия случайной величины X с гамма - распределением определяются по формулам: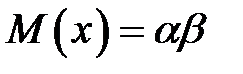 
; 
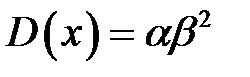
Свойство гамма -распределения: Сумма любого количества независимых гамма-распределенных случайных величин m с одинаковым значением параметра β также подчиняется гамма-распределению, но с параметрами (α1 + а2 +... + ат) и β.
Методы моделирования случайной величины с гамма - распределением
| α | β | Распределения |
| 1 | 1 | экспоненциальное распределение |
| целое | - | распределение Эрланга |
| 0,5 | - | распределение ξ2 |
От случайной величины 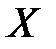, которая имеет гамма - распределение с любым значением параметра α и значением β=1, достаточно легко можно перейти к случайной величине X’ с параметрами α и β > 1. Для этого используется преобразование вида
|
|
|
.
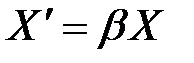Основная проблема, которая возникает при моделировании гамма - распределения, - это вычисление гамма - функции.
Чтобы получить значения гамма - функции можно воспользоваться следующей формулой:
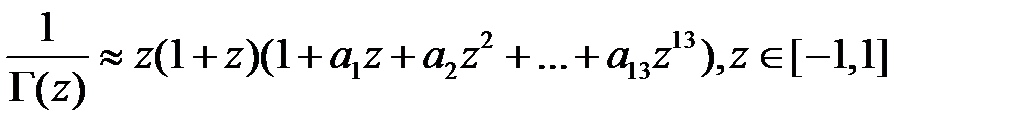
| i | ai | i | ai | i | ai |
| 1 | -0,422784335092 | 5 | -0,017645242118 | 9 | 0,000145624324 |
| 2 | -0,233093736365 | 6 | 0,008023278113 | 10 | -0,000017527917 |
| 3 | 0,191091101162 | 7 | -0,000804341335 | 11 | -0,000002625721 |
| 4 | 0,024552490887 | 8 | -0,000360851496 | 12 | 0,000001328554 |
| 13 | -0,00000018122 |
Вычисление гамма - функции для разных значений ещё усложняется тем, что она зависит от трёх аргументов (x,α,β). Поэтому при моделировании на практике в формуле функции плотности используется неполная гамма-функция
.,
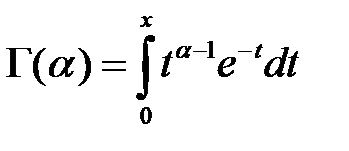для вычисления которой при условии, что α < 1 можно воспользоваться таким выражением:
.
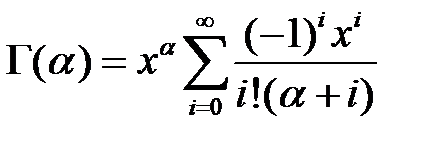Для α > 1 интеграл можно легко вычислить с помощью любых формул численного интегрирования.
Полученная функция плотности гамма - распределения используется для преобразования случайных независимых равномерно распределенных величин. Для этого область возможных значений случайной величины X разбивается на n одинаковых интервалов, количество которых зависит от заданной точности аппроксимации функции f(х). Потом с помощью значения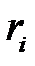 
, (методом розыгрыша по жребию) выбирается один из n интервалов, в котором получают случайные числа с функцией плотности распределения f(х).
Для оценивания близкости функции плотности распределения вероятностей полученных значений случайной величины к функции плотности распределения используют метод наименьших квадратов.
