Арифметическая и геометрическая прогрессии

Теория.

Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий и производной. Приведу основные определения, понятия, таблицы и формулы.

1.1 Проценты.

Определение: один процент – это одна сотая доля. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Пример: 5% от 80 это будет 0,05

r% от 14 это будет 0,01r

При решении задач необходимо понимать механизм начисления процентов по вкладам или кредитам. Например, если банк выдаёт кредит (S) клиенту, то через год клиент должен банку не только сумму кредита, но и некий процент (r). Возникает необходимость введения нового коэффициента b, b=1+0,01r. С учётом этого, долг клиента банку через год можно записать следующим образом:

S + r% от S = S + 0,01r = S (1 + 0,01r) = bS

Платежи.

В задачах по теме «Кредит» используют о три основных вида платежа:

1. Ф иксированные платежи (платежи, которые чётко оговариваются в условии задачи)

2. Аннуитетные платежи (постоянные ежемесячные или ежегодные платежи, которые не меняются на протяжении всего периода кредитования)

3. Дифференцируемые платежи (ежемесячные или ежегодные платежи, уменьшающиеся к концу срока кредитования и обеспечивающие уменьшение суммы долга на одну и ту же величину )

Таблицы.

При решении задач, связанных с аннуитетными платежами мне было очень удобно заполнять следующую таблицу:

S – сумма кредита

r% - годовые (ежемесячные) проценты

b=1+0,01r – коэффициент

х – ежегодная (ежемесячная) выплата

Год	Долг с %	Выплата	Долг после выплаты
0			S
1 год	Sb	x	Sb-x
2 год	(Sb-x)b=Sb²-xb	x	Sb²-xb-x
3 год	(Sb²-xb-x)b=Sb³-x b²-xb	x	Sb³-x b²-xb-x
4 год	(Sb³-x b²-xb-x)b= Sb⁴-xb³-xb²-xb	x	Sb⁴-xb³-xb²-xb-x
5 год	(Sb⁴-xb³-xb²-xb-x)b= Sb⁵-xb^4-xb³-xb²-xb	x	Sb⁵-xb^4-xb³-xb²-xb-x
6 год	(Sb⁵-xb^4-xb³-xb²-xb-x)b= Sb⁶-xb⁵-xb^4-xb-³xb²-xb	x	Sb⁶-xb⁵-xb^4-xb-³xb²-xb-x
n год	Sbⁿ-xbⁿ^-1-xbⁿ^-2-…-xb²-xb	x	Полная выплата, долг равен 0

При решении задач, связанных с дифференцированными платежами я использовала следующую таблицу:

Месяц	Долг с %	Выплата	Долг после выплаты
0			S
1	Sb	Sb
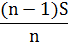
2
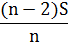
n-1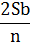
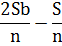
n			0

При решении задач по теме «Вклады»:

Год	Вклад с %
0
1	Sb
2	Sb²
n	Sbⁿ

При решении задач, в которых осуществлялись какие-либо действия (пополнение или снятие денег с вклада):

х – действие

Год	Вклад с %	Действие	Вклад после действия.
0			S
1 год	Sb	+х	Sb+x
2 год	b(Sb+x)= Sb²+xb	+х	Sb²+xb+x
3 год	b(Sb²+xb+x)=Sb^3_+хb²+xb	Снял вклад

Арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Определение. Последовательность чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту же величину, называется арифметической прогрессией.

Любой член арифметической прогрессии вычисляется по формуле:

= + (n-1)d