Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Любой член геометрической прогрессии вычисляется по формуле:
bn =b1· qn-1
Формула суммы n-первых членов геометрической прогрессии
Sn= 
Из этой формулы следует: 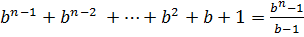
Производная.
Достаточные признаки возрастания и убывания функции:
Если производная данной функции положительна для всех значений х в интервале 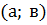 , т.е. f'(x) > 0, то функция в этом интервале возрастает.
, т.е. f'(x) > 0, то функция в этом интервале возрастает.
Если производная данной функции отрицательна для всех значений х в интервале
(а; в), т.е. f'(x) < 0, то функция в этом интервале убывает
Порядок нахождения промежутков монотонности:
Найти область определения функции.
1. Найти производную функции.
2. Найти критические точки (точки, в которых производная не существует) и стационарные (точки, в которых производная равна нулю). Исследовать знак производной в промежутках, на которые найденные точки делят область определения функции.
Достаточное условие существования максимума состоит в смене знака производной при переходе через критическую точку с "+" на "-", а для минимума с "-" на "+". Если при переходе через критическую точку смены знака производной не происходит, то в данной точке экстремума нет
Пример:
f(x) = 
Найдём производную.
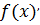 =(
=( ), =
), =  =
=  =
=  =
= 
Критические точки  = 1,
= 1,  = -1
= -1
Стационарные точки 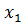 =
=  = -
= -  ,
,  = 0
= 0
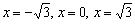

Ответ: возрастает (-  ;+
;+ 
убывает  ; -
; - 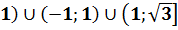
 =
=  ;
;  =
= 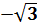 .
.
Практическое решение экономических задач.
Кредиты.
 2020-05-11
2020-05-11 192
192








