2020-05-13
196
Связи между различными явлениями в природе сложны и многообразны, их можно определенным образом классифицировать. В технике и естествознании часто речь идет о функциональной зависимости между переменными х и у, когда каждому возможному значению х поставлено в однозначное соответствие определенное значение у, например, зависимость между давлением и объемом газа (закон Бойля-Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из которых мало, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определенное состояние, а в одно из возможных для нее состояний. Зависимость между величинами Х и У называется статистической, если каждому значению одной переменной соответствует несколько значений другой, встречающихся не одинаково часто. Иными словами, каждому значению одной величины Х соответствует закон распределения другой величины У.
|
|
|
Статистическая зависимость между величинами Х и У называется корреляционной, если изменение величины Х влечет за собой изменение среднего значения величины У.
Пример. Изучается зависимость между величинами Х и У. Каждому значению Х соответствует несколько значений У.
| Х | У |
| 2 | 5, 6, 10 |
| 3 | 6, 10, 12 |
| 4 | 10, 12, 14 |
Условной средней 
называется среднее арифметическое значений У, соответствующих данному значению Х. Так
; 
; 
.
Заметим, что каждому значению величины Х соответствует единственное значение условной средней, т.е. зависимость является функциональной: 
.
Следовательно, корреляционной зависимостью между величинами Х и У называется функциональная зависимость условной средней 
от х. Уравнение зависимости 
называется уравнением регрессии у на х.
График функции 
называется линией регрессии у на х. Аналогично можно вычислить условные средние 
, определить зависимость 
и построить линию регрессии х на у.
В корреляционном анализе решают две основные задачи:
1) Установить форму корреляционной связи, т.е. установить вид функций f(x), φ(y) (линейные, квадратические, показательные и др.).
Для определения вида зависимости в прямоугольной системе координат строят точки, координаты которых (х, у) получены в результате наблюдений. Если точки расположены, например, вблизи некоторой прямой, то корреляцию называют линейной.
2) Оценить тесноту корреляционной связи степенью рассеивания значений у около условной средней 
.
Большое рассеивание свидетельствует о слабой зависимости у от х или об ее отсутствии.
Малое рассеивание свидетельствует о наличии тесной связи между х и у.
|
|
|
Пусть установлено, что зависимость между признаками Х и У имеет линейный характер. Тогда уравнение регрессии может быть представлено в виде:
.
При этом х называется регрессором, угловой коэффициент прямой а 0 называется коэффициентом регрессии у на х и обозначается 
. Если исследуемая зависимость представлена в виде 
, то коэффициент b 0 называется коэффициентом регрессии х на у и обозначается 
. В качестве меры тесноты связи в случае линейной зависимости используют коэффициент корреляции r:
.
Если r > 0, то увеличение одной величины ведет к увеличению другой величины; если r < 0, то увеличение одной величины ведет к уменьшению другой. Если r = 0, то рассматриваемые признаки не связаны линейной зависимостью. Чем больше 
, тем теснее линейная связь между Х и У, и при 
переходит в функциональную. При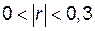 
- связь слабая, при 
- средняя, при 
- сильная, при 
- значительная, почти функциональная. Коэффициент корреляции r, как и другой выборочный показатель, служит оценкой для генерального истинного коэффициента корреляции, его ошибка при п < 100 
. Пусть в результате наблюдений получены значения величин Х и У:
| x i | x 1 | x 2 | … | x n |
| y i | y 1 | y 2 | … | y n |
Уравнение регрессии будем искать в виде: y = a 0 x + a 1. Параметры этого уравнения a 0 и a 1 определим методом наименьших квадратов. Суть метода состоит в следующем. Предположим, что у =f(x) – искомая формула зависимости. Разности f(x i) – y i = εi, i = 1, 2,…, n, назовем отклонениями. Параметры формулы у =f(x) подбирают так, чтобы сумма квадратов отклонений была наименьшей. В рассматриваемой задаче искомая формула f(x)= a 0 x + a 1.
Тогда отклонение εi= a 0xi+ a 1–yi. Согласно методу наименьших квадратов подберем a 0 и a 1 так, чтобы сумма 
была наименьшей. При любых значениях a 0, a 1 функция 
, следовательно, если она имеет экстремум, то это будет минимум.
Необходимые условия экстремума функции двух переменных: 
Или 
Преобразуем систему уравнений к виду:
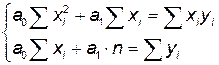
Система называется нормальной системой метода наименьших квадратов. Решить ее можно, например, по правилу Крамера.
Тогда 
, 
, при этом коэффициент а 0 = . Чтобы найти коэффициент регрессии 
, следует в формуле поменять местами х и у: 
.
Коэффициент корреляции r определим по формуле:
.
Ошибку коэффициента корреляции найдем по формуле 
.
Пример. Результаты измерений величин Х и У представлены таблицей:
| x i | 14 | 15 | 16 | 18 | 19 | 17 | 18 | 20 |
| у i | 13,3 | 15,1 | 16,7 | 19,9 | 22,5 | 18,7 | 20,5 | 24,9 |
1) Построить в прямоугольной системе координат заданные точки; убедиться, что величины Х и У связаны линейной зависимостью.
2) Составить уравнение регрессии у(х). Построить полученную прямую.
3) Вычислить коэффициент корреляции r и его ошибку Sr; оценить тесноту связи между Х и У.
Решение. Составим расчетную таблицу:
| xi | yi | xiyi | 
| 
| |
| 14 | 13,3 | 186,2 | 196 | 176,89 | |
| 15 | 15,1 | 226,5 | 225 | 228,01 | |
| 16 | 16,7 | 267,2 | 256 | 279,89 | |
| 18 | 19,6 | 352,8 | 324 | 384,16 | |
| 19 | 22,5 | 427,5 | 361 | 506,25 | |
| 17 | 18,7 | 317,9 | 289 | 349,69 | |
| 18 | 20,5 | 369 | 324 | 420,25 | |
| 20 | 24,9 | 498 | 400 | 620,01 | |
 : 137
| 151,3 | 2645,1 | 2375 | 2964,15 | n = 8 |
Составим нормальную систему уравнений:
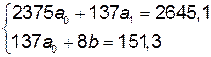
Решим ее по правилу Крамера:
,
,
.
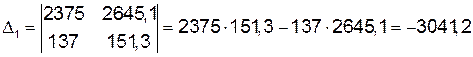Отсюда 
, 
.
Искомое уравнение регрессии у = 1,873 х – 13,165. Для построения полученной прямой найдем две точки:
| х | 1,0 | 20 |
| у | 5,6 | 24,3 |
Коэффициент корреляции найдем по формуле:
, где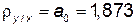 
,
,
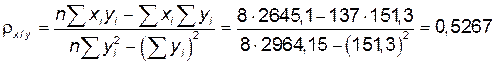. Следовательно, связь между Х и У сильная, почти функциональная. Ошибка коэффициента корреляции:
Построим точки (x i, y i) и прямую линии регрессии.
Рисунок 5.1 – Прямая линия регрессии
Вопросы для самоконтроля.
1. Какие значения может принимать коэффициент корреляции?
2. Как определяется значимость коэффициента корреляции?
3. Что называется регрессией у на х?
4. Как задается парная линейная регрессия?
5. Какой метод используется для вычисления коэффициентов парной линейной регрессии?
|
|
|
6. Как определяются коэффициенты парной линейной регрессии?
Рекомендуемая литература: [1, c.182-186, 253-264], [2, c.190-196].
