Интегральная теорема Муавра-Лапласа

Вероятность того, что в n независимых испытаниях в каждом из которых событие А появляется с постоянной вероятностью р (0 < p < 1), событие А появится не менее m ₁ раз и не более m ₂  раз, приближенно равна

,

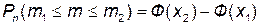где 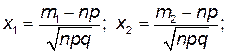 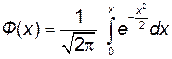– интегральная функция Лапласа, определена для всех 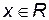, нечетная, табулированная (приложение Б);

;  при .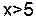

Формула Пуассона  

Если  так, ч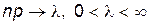то , то

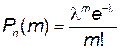
Рассмотрим примеры решения задач с использованием приведенных выше теорем и следствий.

Пример 1. В урне 5 белых и 4 черных шара. Наудачу подряд вынимают 3 шара.  Какова  вероятность  того,  что  среди трех вынутых шаров: 1) два белых; 2) все белые; 3) все черные.

Решение: 1) Пусть событие А: среди 3 вынутых шаров 2 белых. Общее число исходов испытания 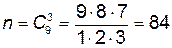, благоприятствуют событию А  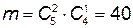исходов. Тогда .

2) Событие B: все вынутые шары – белые; .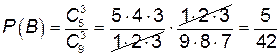

3) Событие D: все вынутые шары – черные; .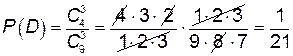

Пример 2. Студент знает 25 вопросов из 30 вопросов программы. Билет содержит 2 вопроса. Какова вероятность, что студент ответит на взятый наудачу билет?

Решение. Событие А: студент знает ответ на оба вопроса взятого наудачу билета; .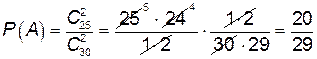

Пример 3. Абонент, набирая номер телефона, забыл 2 последние цифры, но помнит, что они различные. Какова вероятность набрать нужный номер?

Решение. Пусть событие А: набран нужный номер. Всего исходов испытания 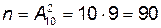. Благоприятствует событию А один исход, т. е. m = 1. Тогда .

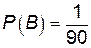Пример 4. Вероятность правильного оформления документов для первого эксперта р ₁ = 0,7; для второго р ₂ = 0,8; для третьего р ₃ = 0,9. Каждый из экспертов оформляет по одному документу. Найти вероятность правильного оформления: а) только одного документа; б) только двух документов; в) всех трех документов; г) хотя бы одного документа.

Решение. Пусть событие А ₁ – первый эксперт оформит документ правильно, р ₁ = 0,7, тогда q ₁ = 0,3; событие А ₂ – второй оформит документ правильно, р ₂=0,8 и q ₂ = 0,2; событие А ₃ – третий оформит документ правильно, р ₃ = 0,9 и q ₃ = 0,1.

а) Событие А – только один (только первый или только второй, или только третий) эксперт оформит документ правильно, тогда:

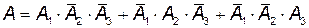
События А ₁, А ₂, А ₃ – независимые, следовательно, события 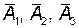 - тоже независимые; события  - несовместные. Используя теоремы умножения и сложения вероятностей, получим

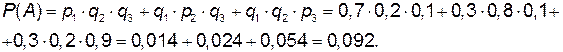
б) Пусть событие В состоит в том, что правильно будут оформлены только 2 документа;

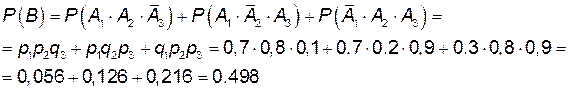
в) Событие С – оформлены правильно все 3 документа:

.

г) Событие D – оформлен правильно хотя бы один документ. Тогда 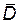 - противоположное событие, состоящее в том, что все документы оформлены неправильно;

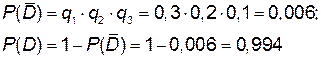
Пример 5. Для посева заготовлены семена пшеницы в основном I сорта, содержащие небольшие количества примесей II, III и IV сорта. Из каждых 100 семян пшеницы в среднем 96 - I сорта, одно - II сорта, два - III сорта и одно - IV сорта. Вероятность того, что из зерна вырастает колос, содержащий не менее 50 зерен, равна 0,5 для зерна I сорта; 0,15 - для II сорта; 0,2 - для III сорта и 0,05 - для IV сорта. Наудачу выбирается одно зерно. Какова вероятность, что колос из данного зерна будет иметь не менее 50 зерен?

Решение. Используем формулу полной вероятности. Относительно наудачу взятого зерна есть гипотезы: В₁ – зерно I сорта, Р(В₁) = 0,96; В₂ – зерно II сорта, Р(В₂) = 0,01; В₃ – зерно III сорта, Р(В₃) = 0,02; В₄ – зерно IV сорта, Р(В₄) = 0,01.

Пусть событие А: колос содержит не менее 50 зерен.

Тогда .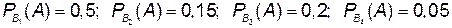

Полная вероятность

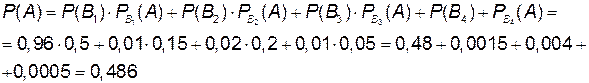
Пример 6. Вероятность того, что расход воды на некотором предприятии окажется нормальным (не более определенного количества литров в сутки) равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход воды будет нормальным любые трое суток.

Решение. Используем формулу Бернулли 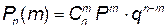, где , .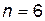

.

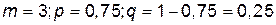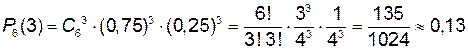Пример 7.  Вероятность всхожести семян данного растения постоянна и равна р = 0,9. Было посажено 2500 семян. Какова вероятность того, что прорастут: а) ровно 2250 семян; б) не более 2200 семян.

Решение. а) Используем локальную теорему Лапласа (приложение А):

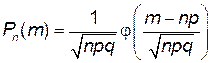, где n =2500, m =2250, p =0,9, q =0,1

Получим: .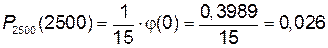

б) Используем интегральную теорему Лапласа (приложение Б):

,

где .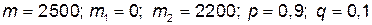

Тогда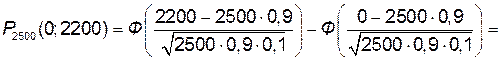

.

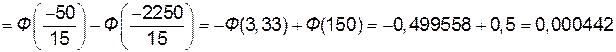Пример 8. Вероятность выпуска бракованного изделия р = 0,015. Найти вероятность того, что среди 400 проверенных изделий бракованных будет ровно пять.

Решение.  Условия  задачи  позволяет  использовать  формулу  Пуассона при  

λ = np = 400∙0,015 = 6. Следовательно:

.

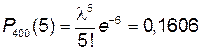Вопросы для самоконтроля.

1. Что называется элементарным событием или элементарным исходом?

2. Что такое пространство элементарных событий?

3. Какое событие называется достоверным, невозможным?

4. Может ли сумма двух событий совпадать с их произведением?

5. Какие события называются несовместными?

6. Какие события называются совместными?

7. Какое событие называется противоположным для данного события?

8. Какие значения может принимать вероятность события?

9. В каком случае вероятность события вычисляется по формуле классической вероятности?

10. Что такое перестановки? Что такое сочетания? Что такое размещения?

11. Как определяется условная вероятность события?

12. Как пересчитать вероятности гипотез после опыта с учётом наблюдаемого результата?

13. В чем заключается определение повторных независимых испытаний?

14. Как найти наиболее вероятное число появлений события в данной серии опытов?

15. При решении каких задач применяется формула Бернулли?

16. Является ли формула Бернулли точной или приближенной?

17. В чем заключается локальная и интегральная теоремы Лапласа?

18. Какие свойства имеют функции j(x) и Ф(x)?

Рекомендуемая литература: [1, c.17-31,c.50-63], [2, c.8-12, c.31-42].

 

2 Случайные величины. Задачи типа 2, 3

Случайной величиной называют такую величину, которая в результате испытания может принять только одно числовое значение из своих возможных значений, заранее неизвестно какое именно, и обусловленное случайными причинами.

Различают дискретные и непрерывные случайные величины. Обозначают случайные величины прописными буквами: X, Y, Z,…, а их возможные значения строчными буквами, например, .

Случайная величина называется дискретной, если она принимает отдельные изолированные значения, которые можно пересчитать, с соответствующими вероятностями. Число значений дискретной случайной величины может быть конечным или бесконечным. Например, дискретная случайная величина Х – число попаданий при трех выстрелах, имеет четыре возможных значения: 0, 1, 2, 3.

Случайная величина называется непрерывной,если ее возможные значения заполняют некоторый интервал полностью. Например, рост человека, вес человека и т.п.

Законом распределения случайной величины называется любое соотношение между возможными значениями случайной величины и соответствующими вероятностями. Эту зависимость можно задать таблично, аналитически или графически.

Если случайная величина Х – дискретная с конечным множеством возможных значений, то ее закон распределения обычно задают в виде таблицы, в первой строке которой указывают все возможные значения случайной величины, расположенные по возрастанию, во второй строке – вероятности, с которыми она их принимает:

x i	x 1	x 2	...	x n
p i	p 1	p 2	...	p n

В этом случае группа событий 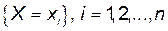 - есть полная группа событий и .

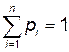Закон распределения дискретной случайной величины можно задать графически в виде многоугольника распределения, если на плоскости построить точки с координатами (x _i, p _i) и соединить их ломаной линией.

Закон распределения непрерывной случайной величины задается интегральной или дифференциальной функциями распределения.

Интегральной функцией распределения F (x) называется функция одного переменного x, определенная на всей числовой оси и для каждого x значение функции F (x) = P (X<x).

Свойства функции F (x):

1) ;

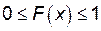2) F (x) – неубывающая функция;

3) .

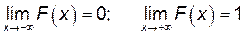4) Вероятность попадания значений случайной величины Х в заданный интер­вал (а; b) определяется по формуле Р (а<Х<b) =F (b) -F (а).

Дифференциальной функцией распределения или плотностью вероятности непрерывной случайной величины Х называется 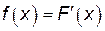. График функции f (x) называется кривой распределения.

Свойства плотности   f (x):

1) 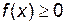, т. к. f (x) есть производная неубывающей функции F (x);

2) 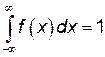, т. к. событие  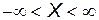 есть достоверное событие;

3) ;

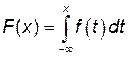4) .

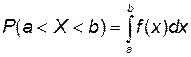Числовые характеристики случайной величины Х:

Математическое ожидание М (Х) случайной величины Х характеризует среднее значение величины Х или среднее ожидаемое значение, или центр распределения случайной величины Х.

Для дискретной случайной величины Х: ;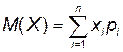

Для непрерывной случайной величины Х: .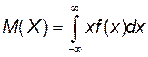

Свойства М (Х):

1. М (С) = С; С = сonst;

2. М (СХ) = С∙М (Х);

3. М (Х+У) = М (Х)+ М (У);

4. М (Х∙У) = М (Х)∙ М (У), если Х и У независимые случайные величины.

Дисперсия D (X) случайной величины Х – мера рассеивания возможных значений Х относительно центра распределения М (Х). D (X) равна математическому ожиданию квадрата отклонения значений Х от М (Х):

.

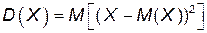Свойства D (X):

1.    для любой случайной величины;

2. D (C) = 0,    C = const.

3. D (CX) = C ²∙ D (X);

4. .

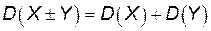Для дискретной случайной величины Х расчетная формула дисперсии:

;

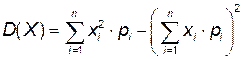для непрерывной величины:

.

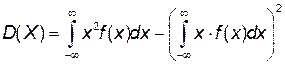Среднее квадратическое отклонение случайной величины Х равно корню квадратному из D (X):   .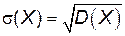

Пример 1. На пути движения автомобиля 4 светофора, каждый из которых с вероятностью р = 0,5 разрешает или запрещает движение автомобиля. Составить закон распределения величины Х – количества светофоров, которые автомобиль минует без остановки. Найти числовые характеристики М, D, 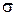 величины Х, построить график F (x) и многоугольник распределения.

Решение. Возможные значения величины Х: 0, 1, 2, 3, 4. Вероятности этих значений найдем по формуле Бернулли при n = 4, p = 0,5 и q = 0,5.

;

;

;

;

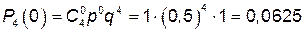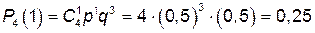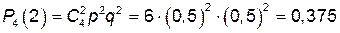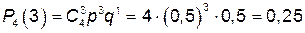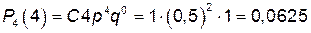.     Проверка: .

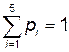Таким образом, закон распределения величины Х:

х i	0	1	2	3	4
р i	0,0625	0,25	0,375	0,25	0,0625

Найдем числовые характеристики дискретной случайной величины Х.

;

.

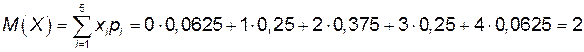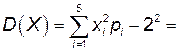
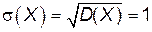Построим многоугольник распределения:

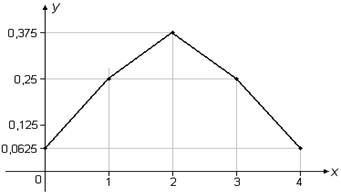
Рисунок 2.1 – Многоугольник распределения

Построим функцию распределения F (x):

1)        ;

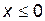
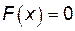2) ;

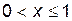
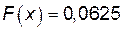3) ;

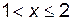
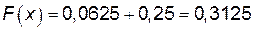4) ;

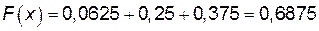5) ;

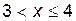
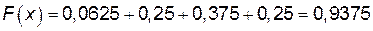6)       

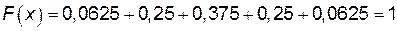
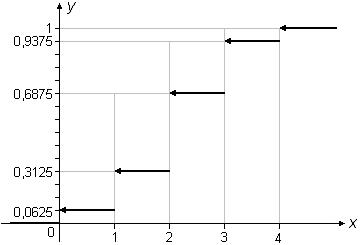
Рисунок 2.2. – График функции F (x)

Пример 2. Случайная величина Х задана интегральной функцией распределения:

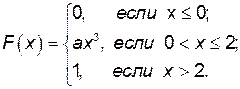
Найти параметр а, плотность вероятности f (x), числовые характеристики М (Х), D (X), 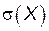. Построить графики функций F (x), f (x).

Решение.

Найдем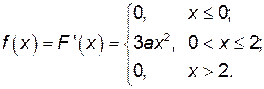

Найдем значение параметра а, используя свойство плотности вероятности:

.

; ; .

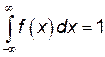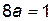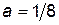Следовательно,    

Тогда функция плотности вероятности

Найдем числовые характеристики случайной величины Х:

;

.

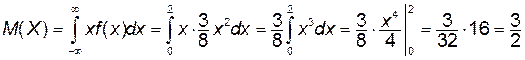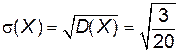Построим графики функций F (x) и f (x):

Рисунок 2.3. – График функции F (x)

Рисунок 2.4. – График функции f (x)

Вопросы для самоконтроля.

1. Что такое случайная величина?

2. Какие случайные величины являются дискретными, непрерывными?

3. Что такое закон распределения случайной величины?

4. Что такое (интегральная) функция распределения случайной величины?

5. Что такое плотность распределения вероятностей случайной величины?

6. Что называется кривой распределения случайной величины?

7. В чем заключается определение закона распределения дискретной случайной величины? Как составляется закон распределения?

8. Какие числовые характеристики имеет дискретная случайная величина? Дать определения.

9. Какие свойства имеет математическое ожидание?

10. Что такое дисперсия, среднее квадратическое отклонение? Какие свойства имеет дисперсия?

11. Математическое ожидание и дисперсия: случайной величины, распределенной по биномиальному закону и закону Пуассона.

12. Что такое функция распределения случайной величины?

13. Какими свойствами обладает функция распределения?

14. Что такое плотность распределения непрерывной случайной величины?

15. Какими свойствами обладает дифференциальная функция?

16. Какие числовые характеристики имеет непрерывная случайная величина?

Рекомендуемая литература: [1, 64-95], [2, c.52-79].