2020-05-13
258
Статистической совокупностью называют множество однородных объектов, объединенных по какому-либо количественному или качественному признаку. Если исследования всей статистической совокупности невозможно, то исследованию подвергают лишь часть ее, которую называют выборочной совокупностью или выборкой. При этом всю совокупность объектов называют генеральной. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Выборка называется репрезентативной (представительной), если она достаточно хорошо представляет свойства генеральной совокупности, для этого выборка должна быть случайной и иметь достаточный объем.
Пусть из генеральной совокупности, объем которой N объектов, извлечена выборка объемом из n объектов для исследования признака Х. Значение Х изменяется при переходе от одного объекта выборки к другому. Это изменение называют вариацией, а значение признака Х для данного объекта – его вариантойх i.
Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке. Вариационный ряд называется дискретным, если варианты принимают отдельные изолированные значения, и непрерывным, если значения вариант полностью заполняют некоторый интервал.
|
|
|
Если признак Х дискретный, то для удобства исследования варианты группируют по отдельным значениям.
Частотой варианты называют число, указывающее, сколько раз встречается значение в выборке; частоту варианты х i обозначают n i, 
, где n – объем выборки.
Относительной частотой варианты х i называется отношение частоты n i к объему выборки n: 
, 
.
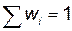Статистическим распределением выборки называется упорядоченный перечень вариант выборки и соответствующих им частот (или относительных частот):
| x i | x 1 | x 2 | … | x k | или | x i | x 1 | x 2 | … | x k | |
| n i | n 1 | n 2 | … | n k | W i | 
| 
| … | 
| ||
Если число вариант n велико или признак Х является непрерывным, составляют интервальный вариационный ряд. Для получения хорошо обозримого вариационного ряда и обеспечения достаточной точности вычисляемых по нему числовых характеристик следует разбить вариацию признака (в пределах от min до max варианты) на такое число классов, чтобы не искажались типичные черты варьирования и ряд получился не слишком растянутым: 
,
где λ – величина классового интервала (шаг по х), k – число классов, на которые необходимо разбить вариацию признака.
Существует формула Стерджеса: k = 1 + 3,32 lg n. Если n > 100, то можно использовать формулу k = 5 lg n (Брукс, Карузерс).
Техника построения вариационного ряда:
1) найдем k;
2) вычислим 
;
|
|
|
3) 
должно попасть примерно в середину первого классового интервала, поэтому нижняя граница первого классового интервала 
. Прибавив 
к 
, получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет 
;
4) верхние границы интервалов уменьшают на величину, равную точности ε, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей;
5) подсчитываем частоты n i.
Чтобы из вариационного интервального ряда получить безинтервальный, нужно взять в качестве вариант серединные значения интервалов, которые называются классовым вариантами в отличие от вариант совокупности.
Если λ = 1, то ряд безинтервальный, классами данного ряда будут сами выстроенные по возрастанию (ранжированные) значения признака.
Пример 1.
Пусть имеем n = 64 значений наблюдаемого количественного дискретного признака Х: 8, 10, 6, 10, 8, 5, 11, 7, 10, 6, 9, 7, 8, 7, 9, 11, 8, 9, 10, 8, 7, 8, 11, 8, 7, 10, 8, 8, 5, 11, 8, 7, 10, 8, 8, 5, 11, 8, 10, 11, 8, 6, 7, 9, 10, 6, 6, 7, 8, 10, 11, 12.
.
Получим вариационный ряд:
| x i | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | , |
| n i | 4 | 7 | 13 | 15 | 7 | 9 | 6 | 3 |
.
Пример 2. Пусть имеем n = 100 значений наблюдаемого количественного непрерывного признака Х:
13,6; 14,7; 13,1; 11,6; 11,9; 12,2; 12,7; 11,5; 14,5; 11,6; 12,9; 10,4;
10,9; 12,4; 10,8; 11,9; 10,5; 12,3; 12,3; 11,9; 12,3; 11,6; 12,0; 11,9;
11,0; 11,6; 11,2; 12,8; 12,6; 12,0; 9,9; 11,7; 11,1; 11,4; 12,6; 10,6;
11,9; 12,6; 11,7; 11,4; 12,7; 12,1; 13,5; 12,8; 10,0; 11,1; 9,7; 12,8;
12,2; 14,7; 11,7; 10,9; 11,2; 11,4; 10,3; 10,7; 13,0; 12,5; 12,3; 11,3;
10,8; 12,1; 13,5; 10,9; 12,7; 12,3; 9,6; 12,8; 11,6; 13,8; 10,4; 9,2;
10,1; 12,7; 11,7; 11,5; 12,5; 11,4; 12,0; 14,3; 10,9; 10,7; 14,0; 13,8;
12,1; 11,2; 11,6; 12,5; 13,5; 13,2; 10,2; 11,5; 10,0; 13,2; 13,8; 11,5;
9,0; 12,3; 12,5; 14,2.
.
Нижняя граница первого классового интервала х н = 9,0 – 0,4 = 8,6.
Классовые интервалы: 8,6 – 9,4 – 10,2 – 11,0 – 11,8 – 12,6 – 13,4 – 14,2 – 15,0.
Уменьшаем верхние границы классовых интервалов на точность ε = 0,1 и вычисляем частоты n i, 
. Срединные значения интервалов найдем по формуле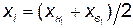 
.
Получим интервальный вариационный ряд:
| № | Классы | Срединные значения | Частоты n i |
| 1 | 8,6 – 9,3 | 9,0 | 2 |
| 2 | 9,4 – 10,1 | 9,8 | 6 |
| 3 | 10,2 – 10,9 | 10,6 | 15 |
| 4 | 11,0 – 11,7 | 11,4 | 23 |
| 5 | 11,8 – 12,5 | 12,2 | 25 |
| 6 | 12,6 – 13,3 | 13,0 | 17 |
| 7 | 13,4 – 14,1 | 13,8 | 7 |
| 8 | 14,2 – 14,9 | 14,6 | 5 |
В этом случае безинтервальный ряд, построенный по интервальным данным, выглядит следующим образом:
| x i | 9,0 | 9,8 | 10,6 | 11,4 | 12,2 | 13,0 | 13,8 | 14,6 |
| n i | 2 | 6 | 15 | 23 | 25 | 17 | 7 | 5 |
Более наглядное изображение закономерности варьирования количественного признака – графики вариационных рядов.
1) Для безинтервального ряда можно построить многоугольник (полигон) распределения, если по оси ОХ откладывать варианты x i (или срединные значения), по оси ОУ – соответствующие частоты n i (или относительные частоты 
). Полученные точки соединить ломаной линией, которая называется вариационной кривой или кривой распределения частот вариационного ряда.
Построим многоугольник (полигон) распределения для вариационного ряда, полученного в примере 1:
| x i | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | , |
| n i | 4 | 7 | 13 | 15 | 7 | 9 | 6 | 3 |
.
Рисунок 4.1 – Полигон распределения частот
2) Графическое изображение интервального вариационного ряда называется гистограммой. По оси ОХ откладываем границы классовых интервалов, по оси ОУ: или а) частоты n i, или б) относительные частоты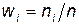 
, или их плотности в) 
, г) 
.
Рассмотрим интервальный вариационный ряд, полученный в примере 2. Построим гистограмму частот n i.. Для каждого классового интервала строим прямоугольник, высотой которого будет величина n i для данного интервала.
Полученная ступенчатая фигура называется гистограммой частот, площадь которой 
.
Если на верхней стороне прямоугольника выделить точкой середину и соединить все такие точки, то получим вариационную кривую частот распределения.
Рисунок 4.2 – Гистограмма частот и вариационная кривая
|
|
|
3) Эмпирической функцией распределения (функцией распределения выборки) называют функцию F *(x), определяющую для каждого значения х относительную частоту события Х < x: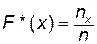 
, где n x – число наблюдений x i, для которых 
, n - объем выборки.
Свойства F *(x) аналогичны свойствам интегральной функции распределения F (x).
F *(x) называется накопленной (кумулятивной) относительной частотой. Для построения графика F *(x) по оси ОХ откладываются классовые интервалы или классовые варианты, по оси ОУ – соответствующие накопленные частоты Sn i.
Если по оси ОХ отложить классовые варианты x i, по оси ОУ – накопленные частоты Sn i и соединить отмеченные точки прямыми отрезками, то полученный график называется кумулятой.
Построим кумуляту для примера 2:
| x i | 9,0 | 9,8 | 10,6 | 11,4 | 12,2 | 13,0 | 13,8 | 14,6 |
| n i | 2 | 6 | 15 | 23 | 25 | 17 | 7 | 5 |
| Sn i | 2 | 8 | 23 | 46 | 71 | 88 | 95 | 100 |
Рисунок 4.3 – График кумуляты частот
Если по оси ОХ отложить накопленные частоты Sn i, по оси ОУ – классовые варианты и соединить отмеченные точки прямыми отрезками, то полученный график называется огивой.
Числовые характеристики статистического распределения выборки
1) Средняя арифметическая (или средняя выборочная) 
- центр распределения, около которого группируются все варианты статистического распределения: 
, где n i – частота варианты х i.
2) Показатели вариации:
- лимиты: х min,, x max;
- размах выборки: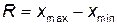 
;
- среднее линейное отклонение: 
;
- дисперсия – среднее арифметическое квадратов отклонений значений х i признака от средней выборочной 
: 
.
Расчетная формула дисперсии: 
.
- среднее квадратическое отклонение 
.
Чтобы упростить расчеты при вычислении 
и 
, переходят к условным вариантам 
, где С – условный («ложный») нуль – варианта с наибольшей частотой; h – шаг для х i для таблиц с равноотстоящим шагом или общий делитель вариант (х i – С) для таблиц с неравноотстоящим шагом. Далее вычисляют 
и 
по формулам 
и 
.
Тогда 
.
Пример. Из генеральной совокупности извлечена выборка объемом n = 100 с равноотстоящими вариантами:
| x i | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| n i | 4 | 11 | 25 | 30 | 15 | 10 | 5 |
Найти: 1) размах выборки;
|
|
|
2) выборочную среднюю;
3) выборочную дисперсию;
4) выборочное среднее квадратическое отклонение;
5) построить полигон распределения частот.
Решение.
1) R = x max – x min = 80 – 20 = 60.
Перейдем к условным вариантам 
, где С – «ложный нуль», С = 50; h = 10.
Составим расчетную таблицу
| x i | n i | x i - C | 
| u i∙ n i | 
| 
| 
|
| 20 | 4 | -30 | -3 | -12 | 9 | 36 | 16 |
| 30 | 11 | -20 | -2 | -22 | 4 | 44 | 11 |
| 40 | 25 | -10 | -1 | -25 | 1 | 25 | 0 |
| 50 | 30 | 0 | 0 | 0 | 0 | 0 | 30 |
| 60 | 15 | 10 | 1 | 15 | 1 | 15 | 60 |
| 70 | 10 | 20 | 2 | 20 | 4 | 40 | 90 |
| 80 | 5 | 30 | 3 | 15 | 9 | 45 | 80 |
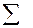
| 100 | -9 | 205 | 287 |
Вычислим 
=-0,09; 
.
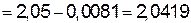2) Найдем 
.
3) 
.
4) 
.
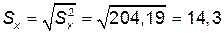Для контроля вычислений используем тождество: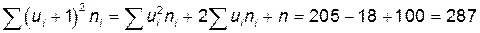 
.
Совпадение контрольных сумм свидетельствует о правильности вычислений.
5) Построим полигон распределения частот. По оси ОХ откладываем варианты х i,, по оси ОУ – частоты n i. Полученные точки соединим ломанной, которая называется вариационной кривой.
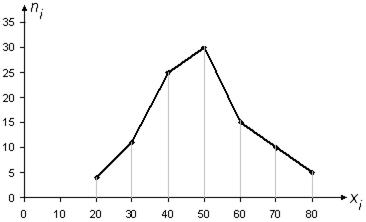
Рисунок 4.4 – Полигон распределения частот
Примечание. 
, , 
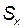являются точечными оценками математического ожидания, дисперсии и среднего квадратического отклонения генеральной совокупности, причем , 
- смещенные оценки. Для получения несмещенных оценок необходимо умножить на поправку Бесселя 
. Полученная оценка дисперсии генеральной совокупности называется исправленной дисперсией:
.
Тогда среднее квадратическое отклонение исправленное 
.Если n велико, то оценки выборочная и исправленная 
практически совпадают.
Вопросы для самоконтроля.
1. Что такое выборка, объем выборки?
2. Что такое генеральная совокупность?
3. Какого типа могут быть результаты наблюдений?
4. Что такое статистический ряд для непрерывных наблюдений; для дискретных наблюдений?
5. Как определяется объем выборки по сгруппированному ряду?
6. Как определяется число классов для интервального ряда?
7. Как представляется графически интервальный ряд?
8. Как представляется графически сгруппированный ряд?
9. Как определяется эмпирическая функция распределения?
10. В каком интервале может принимать значения эмпирическая функция распределения?
11. Чему равна площадь гистограммы, построенной в координатах (x, m), где m – частота?
12. Чему равна площадь гистограммы, построенная в координатах (x, m / n), где m / n – частость?
13. Как определяется среднее арифметическое сгруппированного ряда, интервального ряда?
14. Как определяется выборочная дисперсия для выборки, для сгруппированного ряда, для интервального ряда?
15. Как определяется выборочное среднее квадратическое отклонение?
16. Что такое размах выборки?
Рекомендуемая литература: [1, c.187-196], [2, c.150-152].
