Теоремы умножения вероятностей

1) Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную в предположении, что первое событие произошло:

Р (А · В) = Р (А) · Р_А (В) = Р (В) · Р_В (А)

2) Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Р (А · В) = Р (А) · Р (В)

Теоремы умножения распространяются на любое конечное число событий.

Теоремы сложения вероятностей

1) Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В)

Теорема распространяется на любое конечное число событий.

2) Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного осуществления:

Р (А + В) = Р (А) + Р (В) ― Р (А · В)

Следствия

1) Сумма вероятностей полной группы случайных событий равна единице:

.

2) Два противоположных события А и  образуют полную группу событий, следовательно, имеет место равенство: 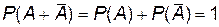. Тогда вероятность противоположного события .

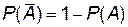3) Пусть имеется n независимых событий А ₁, А ₂, …, А _n;   В – событие, состоящее в том, что в результате испытания появится хотя бы одно из событий А ₁, А ₂, …, А _n. Тогда

.

4) Пусть имеем, например, группу из трех независимых событий А ₁, А ₂,   А ₃, т.е. n = 3; В – событие, состоящее в том, что в результате испытания появится только одно из событий А ₁, А ₂,   А ₃. Тогда

.

5) Формула полной вероятности. Формула Байеса.

Вероятность события А, которое может наступить лишь при условии осуществления одного из несовместных событий (гипотез) В ₁, В ₂,… В _n, образующих полную группу, равна сумме произведений вероятностей гипотез на условные вероятности события А для этих гипотез:

.

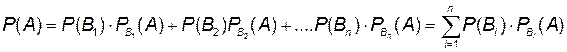Если событие А уже произошло, то вероятности гипотез можно пересчитать по формуле Байеса:

,

где Р (А) есть полная вероятность события А.

Схема испытаний Бернулли  

Пусть проводится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < p < 1). Вероятность непоявления события А:   q = 1 – p.

 Формула Бернулли позволяет вычислить вероятность появления события А ровно m раз в n независимых испытаниях: .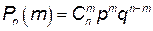

Следствия из формулы Бернулли

Вероятность появления события А в n испытаниях схемы Бернулли:

а) менее m раз: ;

б) не менее m раз:

или:                     

в) более m раз: ;

г) не более m раз:

д) от m ₁ до m ₂ раз: .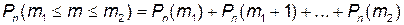

Во многих случаях необходимо найти наивероятнейшее число m ₀ появлений события А, т. е. такое целое число m ₀, вероятность которого Р _n(m ₀) наибольшая среди других вероятностей Р _n(m). Это значение m ₀ определяется соотношением

.

Вычисление вероятностей ,  по формуле Бернулли усложняется при больших n и малых p или q. В таких случаях используют приближенные (асимптотические) формулы.