Тема 6 дискретная случайная величина

Дискретной называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным. Дискретная случайная величина может быть задана рядом распределения — это соответствие между возможными значениями и их вероятностями:

Х			…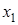
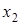
Р			…

, .

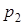
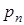
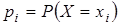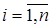События 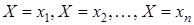 образуют полную группу, следовательно, сумма вероятностей этих событий равна единице: .

Ряд распределения дискретной случайной величины можно изобразить графически в виде полигона или многоугольника распределения вероятностей. Для этого по горизонтальной оси в выбранном масштабе нужно отложить значения случайной величины, а по вертикальной — вероятности этих значений, тогда точки с координатами  будут изображать полигон распределения вероятностей; соединив же эти точки отрезками прямой, получим многоугольник распределения вероятностей. Дискретная случайная величина может быть задана функцией распределения. Функцией распределения случайной величины Х называется функция 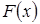, выражающая для каждого х вероятность того, что случайная величина Х примет значение меньшее х: 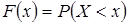. Функцию  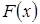иногда называют интегральной функцией распределения.

Интегральная функция распределения F (x) обладает свойствами:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: .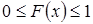

2. Функция распределения есть неубывающая функция на всей числовой оси.

3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна 1, т.е. ; .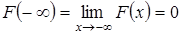

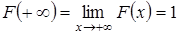4. Вероятность попадания случайной величины в интервал 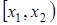 (включая 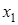) равна приращению ее функции распределения на этом интервале, т.е.

.

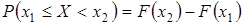Математическое ожидание М (Х) дискретной случайной величины

Пусть случайная величина Х может принимать только значения , вероятности которых соответственно равны 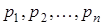. Тогда математическое ожидание М (Х) случайной величины Х определяется равенством: .

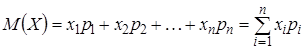Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Математическое ожидание приближенно равно среднему арифметическому значений случайной величины: .