Свойства математического ожидания

1. Математическое ожидание постоянной величины равно самой посто­янной: .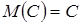

2. Постоянный множитель можно выносить за знак математического ожидания: .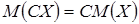

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий:

.

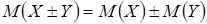4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий:

.

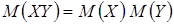5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: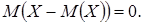

Дисперсия случайной величины

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Дисперсией 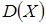 случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:

.

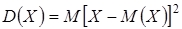Дисперсия — это мера рассеяния случайной величины около ее математического ожидания. Если Х — дискретная случайная величина, то дисперсию вычисляют по следующим формулам: 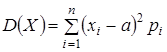, где а = М (Х); .

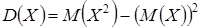Свойства дисперсии случайной величины

1. Дисперсия постоянной величины С равна нулю: .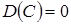

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: .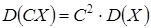

3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: .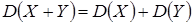

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: .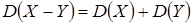

Средним квадратическим отклонением 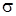 случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии: 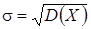. Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.