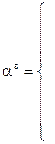Движение АЗ при выходе на высоту дрейфа и в свободном дрейфе в атмосфере существенно зависит от теплообмена между подъемным газом и внешней средой, так как температура и давление газа в аэростатной оболочке определяют объем и, следовательно, аэростатическую силу аэростата. Математическое описание реальных тепловых процессов, имеющих место при свободном дрейфе аэростата, – достаточно сложная задача. Для ее упрощения в данной тепловой модели приняты следующие допущения и предположения:
· распределение температур оболочки аэростата и стенки баллона высокого давления по поверхности и толщине оболочки и стенки баллона принято равномерным;
· параметры состояния подъемного газа в оболочке аэростата
и в баллонах высокого давления постоянны по всему объему;
· истечение подъемного газа через диафрагму при наполнении является адиабатическим, потери тепла в трубопроводе наполнения отсутствуют, и подъемный газ на входе в оболочку имеет температуру газа в баллонах высокого давления;
· изменение внутренней энергии подъемного газа в баллонах высокого давления происходит за счет работы и массообмена дросселирования (при наполнении), а также за счет теплообмена свободной конвекцией со стенками баллонов;
· изменение внутренней энергии баллонов высокого давления
осуществляется за счет теплообмена свободной конвекцией с газом
внутри баллонов и конвекцией с окружающей средой;
· изменение внутренней энергии подъемного газа в оболочке аэростата происходит за счет работы и массообмена дросселирования (при наполнении и потерях газа в процессе дрейфа), теплообмена свободной конвекцией с оболочкой аэростата и работы атмосферы по сжатию (расширению) подъемного газа;
· подъемный газ считается полностью оптически прозрачным для всех видов излучения, а его собственное излучение отсутствует;
· изменение внутренней энергии оболочки аэростата осуществляется за счет теплообмена свободной конвекцией с подъемным газом внутри оболочки, конвекцией с окружающей средой, а также за счет излучения атмосферы и поверхности планеты и собственного излучения оболочки.
С учетом этого тепловой режим аэростата описывается следующими уравнениями:
|
|
| ||||
|
|
| ||||
|
|
| ||||
|
| при |
| |||
| при |
| ||||
| где | 
| – удельная теплоемкость подъемного газа при постоянном давлении; |

| – удельная теплоемкость; | |

| – температура оболочки; | |
 
| – температура атмосферы; | |

| – поверхность оболочки, участвующая в теплообмене; | |

| – масса оболочки, участвующая в теплообмене; | |
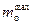
| – масса оболочки; | |

| – постоянная Стефана-Больцмана; | |

| – излучательная способность; | |
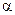
| – коэффициент поглощения оболочки; | |

| – солнечный поток; | |

| – поверхностная масса оболочки; | |
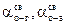
| – коэффициенты теплоотдачи при свободной конвекции между оболочкой и газом, оболочкой и атмосферой; | |

| – коэффициент теплоотдачи при вынужденной конвекции между оболочкой и атмосферой. |
Коэффициент теплоотдачи при свободной конвекции – функция числа Релея Rа:
|
| 
| при |  , ,
| |

| при | 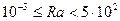 , ,
| ||

| при |  , ,
| ||
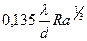
| при |  . .
|
Коэффициент теплоотдачи при вынужденной конвекции – функция числа Рейнольдса Rе:
|
|
| при |  , ,
|
| ||||
|
| при | 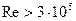 , ,
| ||||||
| где |
| – коэффициент теплопроводности; | ||||||
|
|
| – диаметр оболочки.
| ||||||
 2020-05-11
2020-05-11 309
309

 ,
,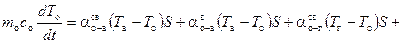
 ,
,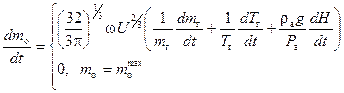
 ,
, ,
,