Анализ процесса ввода аэростатных станций в действие и дрейфа в атмосфере, а также послеполетная обработка результатов штатного (или нештатного) функционирования могут быть проведены только с использованием математических моделей, отражающих движение аэростата, теплообмен между газом в оболочке и окружающей средой. При этом необходимо учитывать реальные характеристики оболочки аэростата, полученные в результате наземных испытаний, и широкий спектр различных возмущающих воздействий.
Именно с учетом вышеизложенных рассуждений для исследований процессов, связанных с вводом АЗ, в данном пособии был определен состав математической модели как совокупности следующих ее составных частей:
· модель движения;
· размерно-массовая модель;
· тепловая модель;
· аэродинамическая модель.
При формировании математических моделей принимались допущения, предельно упрощающие математические описания с целью выделения наиболее значимых для данных исследований факторов.
Модель движения
Процесс движения АЗ в атмосфере состоит из следующих основных участков:
· участок аэродинамического торможения в составе спускаемого аппарата;
· участок совместного движения АЗ с верхней полусферой на парашюте увода;
· участок движения на аэростатной парашютной системе, в процессе которого осуществляются развертывание и наполнение оболочки аэростата газом;
· участок движения аэростата с балластом;
· участок выхода на высоту дрейфа;
· дрейф аэростатной станции на высоте аэростатического равновесия.
Особое внимание при формировании модели с учетом объекта исследования уделено заключительному этапу функционирования АЗ и обеспечению ввода его в действие. Для оценки процесса дрейфа, возможности управлять им и правильной интерпретации полученных во время отработки экспериментальных данных разработана математическая модель АЗ, достаточно полно описывающая как номинальное, так и возмущенное движение аэростата при дрейфе [16].
Движение АЗ на парашютной системе. Математическое описание динамики полета АЗ в атмосфере, в общем случае пространственного движения, приводит к чрезвычайно громоздкой системе дифференциальных уравнений. Для проведения качественных исследований с целью выявления основных закономерностей целесообразно использовать систему уравнений, записанных при таких упрощающих допущениях:
· движение около центра масс не рассматривается;
· планета имеет форму шара с радиусом 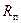 ;
;
· поле тяготения центральное;
· не рассматривается движение под действием горизонтальной компоненты ветра.
К основным силам, действующим на АЗ при его движении в атмосфере относятся:
· сила тяжести 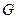 ;
;
· аэродинамическая сила 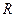 ;
;
· аэростатическая подъемная сила 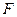 .
.
Действие других сил, например центростремительной силы, обусловленной кривизной поверхности планеты, силы Кориолиса, притяжения Солнца и других небесных тел, мало по сравнению с действием основных сил и в математической модели не учитывается.
Сила тяжести G, обусловленная взаимным притяжением тел, обладающих массой, согласно закону всемирного тяготения с учетом принятой сферической модели гравитационного поля планеты может быть выражена следующим образом:
|
| 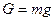 , ,
| ||
| где |
| ||
|
| |||
|
| |||
|
| |||
|
| |||
Аэродинамическая сила R является равнодействующей сил давления и трения, возникающих при движении АЗ относительно воздушной среды, и зависит от формы и размеров оболочки аэростата, числа Рейнольдса 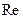 , угла атаки
, угла атаки 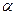 .
.
В общем случае эта сила раскладывается на две составляющие (сила лобового сопротивления и аэродинамическая подъемная сила), величина которых определяется соответствующими коэффициентами
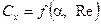 , ,
| ||
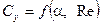 . .
|
Аэростатическая подъемная сила 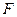 может быть представлена выражением:
может быть представлена выражением:
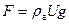 , ,
| ||
| где | ||
|
| ||
Уравнения движения. С учетом принятых допущений уравнения движения АЗ а в атмосфере в проекциях на оси скоростной системы координат имеют вид:
|
| 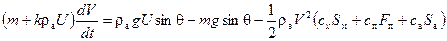 , ,
| ||||
|
| 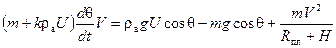 , ,
| ||||
|
| 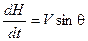 , ,
| ||||
|
| 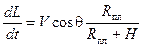 , ,
| ||||
| где | 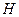
| – высота над нулевым уровнем поверхности; | |||
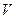
| – скорость аппарата; | ||||
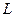
| – дальность; | ||||
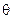
| – траекторный угол; | ||||
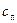
| – коэффициент аэродинамического сопротивления парашюта; | ||||
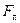
| – площадь парашюта; | ||||
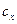
| – коэффициент сопротивления аэростата; | ||||
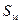
| – характерная площадь аэростата; | ||||
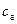
| – коэффициент аэродинамического сопротивления АЗ; | ||||
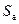
| – площадь миделя АЗ; | ||||
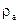
| – плотность атмосферы; | ||||
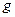
| – ускорение силы тяжести на высоте | ||||
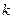
| – коэффициент присоединенной массы. | ||||
Участок дрейфа АЗ в атмосфере. При движении в атмосфере АЗ отслеживает различные атмосферные возмущения: ветер, изменения плотности в результате колебаний температуры и давления, гравитационные волны (одновременное изменение вертикального ветра и плотности атмосферы по синусоидальному закону), а также изменения состояния подъемного газа и оболочки аэростата (перегрев газа в оболочке, утечка газа через оболочку). Математическая модель представляет собой систему дифференциальных уравнений движения центра масс АЗ в проекции на оси принятой системы координат.
На участке дрейфа в атмосфере вертикальное движение аэростата как материальной точки под действием сил веса, подъемной силы и силы лобового сопротивления описывается уравнением:
|
| 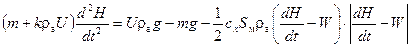 , ,
| ||||
| где | 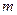
| – масса аэростата (вместе с массой подъемного газа); | |||
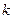
| – коэффициент присоединенной массы; | ||||
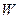
| – скорость вертикального ветра; | ||||
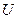
| – объем аэростата. | ||||
Для участка выхода АЗ на дрейф, когда скорость вертикального ветра W мала по сравнению со скоростью аппарата V, принято V в = - V. Так как объем зонда мал по сравнению с объемом аэростата, то до момента начала наполнения оболочки аэростата принимается U = 0.
Данная система уравнений дополняется уравнениями, описывающими состояние атмосферы:
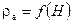 ,
, 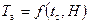 ,
,
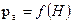 ,
,
| где | 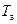 – температура атмосферы; – температура атмосферы;
|
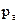 – давление атмосферы; – давление атмосферы;
| |
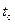 – время суток. – время суток.
|
В модели учитывались реальные характеристики оболочки аэростата, полученные в результате наземных испытаний:
· диаграмма растяжения материала оболочки в зависимости от избыточного давления (см. размерно-массовую модель), при этом зависимость объема оболочки от избыточного давления принимаем линейной, пренебрегая небольшим гистерезисом, что для малых аэростатов оправдано и не вносит существенной погрешности в расчеты;
· аэродинамические характеристики в зависимости от режима обтекания оболочки – ламинарный или турбулентный (см. аэродинамическую модель – зависимость 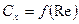 );
);
· газопроницаемость оболочки (см. размерно-массовую модель);
· устойчивость аэростата от величины избыточного давления (под устойчивостью понимаем стремление аэростата вернуться на исходную высоту статического равновесия после прекращения действия возмущающего фактора);
· влияние режима обтекания оболочки на реакцию аэростата.
Учитывались также такие возмущающие воздействия (для Венеры, например), как:
1) вертикальные порывы ветра, заданные в виде прямоугольного импульса:
а) с амплитудой
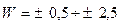 м/с, (
м/с, (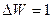 м/с)
м/с)
(знак «+» соответствует порыву ветра, направленному вниз), и временем действия ветра t = 45 мин, для различных значений коэффициента 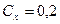 и
и 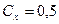 , а также с учетом режима обтекания оболочки
, а также с учетом режима обтекания оболочки 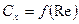 ;
;
б) изменение плотности атмосферы в результате вариаций температуры и давления (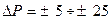 мм. рт. ст.,
мм. рт. ст., 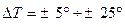 );
);
в) влияние солнечного потока на высоту дрейфа аэростатной станции с целью определения изменения высоты дрейфа при переходе с ночной стороны планеты на дневную в результате перегрева газа в оболочке для различных значений зенитного угла Солнца 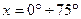 , (
, (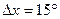 );
);
2) заданные в виде синусоидальных колебаний:
а) вертикальные порывы ветра с амплитудой 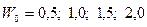 м/с
м/с
и периодом колебаний 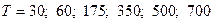 с;
с;
б) гравитационные волны 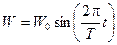 ,
, 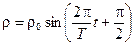
с разностью фаз между ветром и плотностью 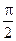 .
.
Изменение массовых, аэродинамических и геометрических характеристик АЗ, входящих в уравнения движения, осуществляется в соответствии с принятой схемой выхода на дрейф.
 2020-05-11
2020-05-11 375
375

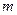 – масса АЗ;
– масса АЗ;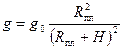 – ускорение свободного падения;
– ускорение свободного падения;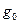 – ускорение свободного падения на поверхности планеты;
– ускорение свободного падения на поверхности планеты;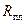 – радиус планеты;
– радиус планеты;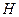 – высота от поверхности планеты.
– высота от поверхности планеты.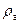 – плотность атмосферы на высоте Н;
– плотность атмосферы на высоте Н;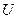 – объем оболочки аэростата.
– объем оболочки аэростата.






