Оценка проектных параметров с использованием метода эквивалентных возмущений

Математически задача исследования точности динамической системы формируется как задача определения законов распределения или статистических характеристик случайных величин или случайных функций. Задача исследования точности в настоящее время наиболее полно и в достаточно общем виде решена для линейных систем [17].

Наиболее употребительными методами приближенной теоретико-вероятностной оценки точности работы нелинейных динамических систем являются метод статистических испытаний (метод Монте-Карло) и метод эквивалентных возмущений (метод Доступова).

Наименее трудоёмким является метод эквивалентных возмущений, нашедший широкое практическое применение в технике для приближенного вероятностного анализа состояния систем.

Точность метода эквивалентных возмущений определяется порядком принятой аппроксимации, а объем необходимых расчетов зависит от степени q аппроксимирующего полинома и числа 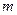 возмущений. Ниже приведены расчетные формулы для определения математического ожидания и дисперсии для степеней аппроксимирующего полинома  и .

Степень аппроксимирующего полинома .

Математическое ожидание координаты :

,

где  – решение исходной системы при подстановке вместо случайных параметров  неслучайных величин 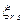 в соответствии с                    Таблица1.

Дисперсия координаты

              Таблица1.

Определение неслучайных величин  при .

	1	2	3
1		0	0		0	0
2	0		0		0	0
3	0	0			0	0
	0	0	0		0

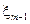
Степень аппроксимирующего полинома .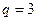

Математическое ожидание координаты :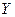

,

где  – решения исходной системы при подстановке вместо случайных параметров  неслучайных величин  и .

;

.

Дисперсия координаты :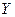

.

При , .

Выражение для математического ожидания приобретает следующий вид:

,

где .